Article contents
Generalized Lagrangian heterogeneous multiscale modelling of complex fluids
Published online by Cambridge University Press: 10 August 2023
Abstract
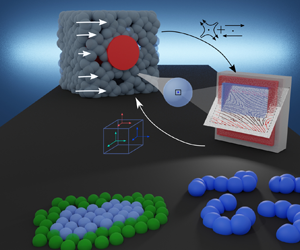
We introduce a fully Lagrangian heterogeneous multiscale method (LHMM) to model complex fluids with microscopic features that can extend over large spatio/temporal scales, such as polymeric solutions and multiphasic systems. The proposed approach discretizes the fluctuating Navier–Stokes equations in a particle-based setting using smoothed dissipative particle dynamics (SDPD). This multiscale method uses microscopic information derived on-the-fly to provide the stress tensor of the momentum balance in a macroscale problem, therefore bypassing the need for approximate constitutive relations for the stress. We exploit the intrinsic multiscale features of SDPD to account for thermal fluctuations as the characteristic size of the discretizing particles decreases. We validate the LHMM using different flow configurations (reverse Poiseuille flow, flow passing a cylinder array and flow around a square cavity) and fluid (Newtonian and non-Newtonian). We show the framework's flexibility to model complex fluids at the microscale using multiphase and polymeric systems. We also show that stresses are adequately captured and passed from micro to macro scales, leading to richer fluid response at the continuum. In general, the proposed methodology provides a natural link between variations at a macroscale, whereas accounting for memory effects of microscales.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 8
- Cited by


