Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T01:26:01.598Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalized vortex ring model

Published online by Cambridge University Press:  10 March 2009

FELIX KAPLANSKI ,
SERGEI S SAZHIN ,
YASUHIDE FUKUMOTO ,
STEVEN BEGG  and
MORGAN HEIKAL
FELIX KAPLANSKI
Affiliation:
Laboratory of Multiphase Physics, Tallinn University of Technology, Tallinn 19086, Estonia
SERGEI S SAZHIN*
Affiliation:
School of Environment and Technology, Faculty of Science and Engineering, The University of Brighton, Brighton BN2 4GJ, UK
YASUHIDE FUKUMOTO
Affiliation:
Graduate School of Mathematics and Mathematical Research Centre for Industrial Technology, Kyushu University 33, Fukuoka 812-8581, Japan
STEVEN BEGG
Affiliation:
School of Environment and Technology, Faculty of Science and Engineering, The University of Brighton, Brighton BN2 4GJ, UK
MORGAN HEIKAL
Affiliation:
School of Environment and Technology, Faculty of Science and Engineering, The University of Brighton, Brighton BN2 4GJ, UK
*
†Email address for correspondence: s.sazhin@brighton.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

A conventional laminar vortex ring model is generalized by assuming that the time dependence of the vortex ring thickness ℓ is given by the relation ℓ = atb, where a is a positive number and 1/4 ≤ b ≤ 1/2. In the case in which 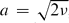, where ν is the laminar kinematic viscosity, and b = 1/2, the predictions of the generalized model are identical with the predictions of the conventional laminar model. In the case of b = 1/4 some of its predictions are similar to the turbulent vortex ring models, assuming that the time-dependent effective turbulent viscosity ν∗ is equal to ℓℓ′. This generalization is performed both in the case of a fixed vortex ring radius R0 and increasing vortex ring radius. In the latter case, the so-called second Saffman's formula is modified. In the case of fixed R0, the predicted vorticity distribution for short times shows a close agreement with a Gaussian form for all b and compares favourably with available experimental data. The time evolution of the location of the region of maximal vorticity and the region in which the velocity of the fluid in the frame of reference moving with the vortex ring centroid is equal to zero is analysed. It is noted that the locations of both regions depend upon b, the latter region being always further away from the vortex axis than the first one. It is shown that the axial velocities of the fluid in the first region are always greater than the axial velocities in the second region. Both velocities depend strongly upon b. Although the radial component of velocity in both of these regions is equal to zero, the location of both of these regions changes with time. This leads to the introduction of an effective radial velocity component; the latter case depends upon b. The predictions of the model are compared with the results of experimental measurements of vortex ring parameters reported in the literature.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 622 , 10 March 2009 , pp. 233 - 258
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Afanasyev, Y. D. & Korabel, V. N. 2004 Starting vortex dipoles in a viscous fluid: asymptotic theory, numerical simulation, and laboratory experiments. Phys. of Fluids 16 (11), 3850–3858.CrossRefGoogle Scholar
Batchelor, G. K. (1967) An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Berezovski, A. & Kaplanski, F. 1995 Vorticity distributions for thick and thin vortex pairs and rings. Arch. Mech. 47 (6), 1015–1026.Google Scholar
Cantwell, B. 2002 Introduction to Symmetry Analysis. Cambridge University Press.Google Scholar
Dabiri, J. O. & Gharib, M. 2004 Fluid entrainment by isolated vortex rings. J. Fluid Mech. 511, 311–331.CrossRefGoogle Scholar
Fukumoto, Y. & Kaplanski, F. 2008 Global time evolution of an axisymmetric vortex ring at low Reynolds numbers. Phys. of Fluids 20, 053103.CrossRefGoogle Scholar
Fukumoto, Y. & Moffatt, H. K. 2000 Motion and expansion of a viscous vortex ring. Part 1. A higher-order asymptotic formula for the velocity. J. Fluid Mech. 417, 1–45.CrossRefGoogle Scholar
Glezer, A. & Coles, D. 1990 An experimental study of a turbulent vortex ring J. Fluid Mech. 211, 243–283.CrossRefGoogle Scholar
Helmholtz, H. 1858 On integrals of the hydrodynamical equations which express vortex-motion. Crelle's J. 55, 485–512.Google Scholar
Kaltaev, A. 1982 Investigation of dynamic characteristics of a vortex ring of viscous fluid (in Russian). In Continuum Dynamics, pp. 63–70. Kazan State University.Google Scholar
Kambe, T. & Oshima, Y. 1975 Generation and decay of viscous vortex rings J. Phys. Soc. Jpn 38, 271–280.CrossRefGoogle Scholar
Kaplanski, F. & Rudi, U. 1999 Dynamics of a viscous vortex ring. Intl J. Fluid Mech. Res. 26, 618–630.CrossRefGoogle Scholar
Kaplanski, F. & Rudi, Y. 2005 A model for the formation of ‘optimal’ vortex rings taking into account viscosity. Phys. Fluids 17, 087101–087107.CrossRefGoogle Scholar
Kovasznay, L. S. G., Fujita, H. & Lee, R. L. 1974 Unsteady turbulent puffs. Adv. Geophys. 18B, 253–263.Google Scholar
Lamb, H. 1932 Hydrodynamics, 6th edition. Dover.Google Scholar
Lavrentiev, M. A. & Shabat, B. V. 1973 Problems of Hydrodynamics and Mathematical Models. Nauka.Google Scholar
Lim, T. & Nickels, T. 1995 Vortex rings. In Fluid Vortices (ed. Green, S. I.). Kluwer.Google Scholar
Linden, P. E. & Turner, J. S. 2001 The formation of ‘optimal’ vortex rings, and the efficiency of propulsion devices. J. Fluid Mech. 427, 61–72.CrossRefGoogle Scholar
Lugovtsov, B. A. 1970 On the motion of a turbulent vortex ring and its role in the transport of passive contaminant. In Some Problems of Mathematics and Mechanics. Nauka.Google Scholar
Lugovtsov, B. A. 1976 On the motion of a turbulent vortex ring. Arch. Mech. 28, 759–766.Google Scholar
Mathematica 2007 Version 6.0.0. http://functions.wolfram.com.Google Scholar
Maxworthy, T. 1972 The structure and stability of virtex rings. J. Fluid Mech. 51, 15–32.CrossRefGoogle Scholar
Maxworthy, T. 1974 Turbulent vortex rings (with an appendix on an extended theory of laminar vortex rings). J. Fluid Mech. 64, 227–239.CrossRefGoogle Scholar
Maxworthy, T. 1977 Some experimental studies of vortex rings. J. Fluid Mech. 81, 465–495.CrossRefGoogle Scholar
Mohseni, K. 2001 Statistical equilibrium theory of axisymmetric flows: Kelvin's variational principle and an explanation for the vortex ring pinch-off process. Phys. Fluids 13, 1924–1931.CrossRefGoogle Scholar
Mohseni, K. 2006 A formulation for calculating the translational velocity of a vortex ring or pair. Bioinspir. Biomim. 1, S57–S64.CrossRefGoogle ScholarPubMed
Mohseni, K. & Gharib, M. 1998 A model for universal time scale of vortex ring formation. Phys. Fluids 10, 2436–2438.CrossRefGoogle Scholar
Norbury, J. 1973 A family of steady vortex rings. J. Fluid Mech. 57, 417–431.CrossRefGoogle Scholar
Panton, R. L. 1996 Incompressible Flow. John Wiley.Google Scholar
Phillips, O. M. 1956 The final period of decay of non-homogeneous turbulence. Proc. Camb. Phil. Soc. 252, 135–151.CrossRefGoogle Scholar
Rott, N. & Cantwell, B. 1993 a Vortex drift. Part 1. Dynamic interpretation Phys. Fluids A 5, 1443–1450.CrossRefGoogle Scholar
Rott, N. & Cantwell, B. 1993 b Vortex drift. Part 2.. The flow potential surrounding a drifting vortical region. Phys. Fluids A 5, 1451–1455.CrossRefGoogle Scholar
Saffman, P. G. 1970 The velocity of viscous vortex rings. Stud. Appl. Math. 49, 371–380.CrossRefGoogle Scholar
Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
Sazhin, S. S., Kaplanski, F., Feng, G., Heikal, M. R. & Bowen, P. J. 2001 A fuel spray induced vortex ring. Fuel 80, 1871–1883.CrossRefGoogle Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.CrossRefGoogle Scholar
Shusser, M. & Gharib, M. 2000 Energy and velocity of a forming vortex ring. Phys. Fluids 12, 618–621.CrossRefGoogle Scholar
Stanaway, S., Cantwell, B. J. & Spalart, P. R. 1988 A numerical study of viscous vortex rings using a spectral method. Tech. Memo. 101041. NASA.Google Scholar
Wang, C.-T, Chu, C.-C. & Chien-Chang, 1994 Initial motion of a vortex ring. Proc. R. Soc. London A 446, 589–599.Google Scholar
Weigand, A. & Gharib, M. 1997 On the evolution of laminar vortex rings. Exps Fluids 22, 447–457.CrossRefGoogle Scholar