Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-31T20:50:51.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Global stability of multiple solutions in plane sudden-expansion flow

Published online by Cambridge University Press:  16 May 2012

Daniel Lanzerstorfer  and
Hendrik C. Kuhlmann
Daniel Lanzerstorfer
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, Vienna University of Technology, Resselgasse 3, A-1040 Vienna, Austria
Hendrik C. Kuhlmann*
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, Vienna University of Technology, Resselgasse 3, A-1040 Vienna, Austria
*
†Email address for correspondence: h.kuhlmann@tuwien.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

The two-dimensional, incompressible flow in a plane sudden expansion is investigated numerically for a systematic variation of the geometry, covering expansion ratios (steps-to-outlet heights) from 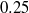to 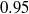. By means of a three-dimensional linear stability analysis global temporal modes are scrutinized. In a symmetric expansion the primary bifurcation is stationary and two-dimensional, breaking the mirror symmetry with respect to the mid-plane. The secondary asymmetric flow experiences a secondary instability to different three-dimensional modes, depending on the expansion ratio. For a moderately asymmetric expansion only one of the two secondary flows (the connected branch) is realized at low Reynolds numbers. Since the perturbed secondary flow does not deviate much from the symmetric secondary flow, both secondary stability boundaries are very close to each other. For very small and very large expansion ratios an asymptotic behaviour is found for suitably scaled critical Reynolds numbers and wavenumbers. Representative instabilities are analysed in detail using an a posteriori energy transfer analysis to reveal the physical nature of the instabilities. Depending on the geometry, pure centrifugal and elliptical amplification processes are identified. We also find that the basic flow can become unstable due to the effects of flow deceleration, streamline convergence and high shear stresses, respectively.

JFM classification

Instability: Instability Instability: Transition to turbulence

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 702 , 10 July 2012 , pp. 378 - 402
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1. Alleborn, N., Nandakumar, K., Raszillier, H. & Durst, F. 1997 Further contributions on the two-dimensional flow in a sudden expansion. J. Fluid Mech. 330, 169–188.CrossRefGoogle Scholar
2. Battaglia, F., Tavener, S. J., Kulkarni, A. K. & Merkle, C. L. 1997 Bifurcation of low Reynolds number flows in symmetric channels. AIAA Journal 35 (1), 99–105.CrossRefGoogle Scholar
3. Bayly, B. J. 1988 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31, 56–64.CrossRefGoogle Scholar
4. Cherdron, W., Durst, F. & Whitelaw, J. H. 1978 Asymmetric flows and instabilities in symmetric ducts with sudden expansions. J. Fluid Mech. 84 (1), 13–31.CrossRefGoogle Scholar
5. Chiang, T. P., Sheu, T. W. H., Hwang, R. R. & Sau, A. 2001 Spanwise bifurcation in plane-symmetric sudden-expansion flows. Phys. Rev. E 65, 1–16.CrossRefGoogle ScholarPubMed
6. Chiang, T. P., Sheu, T. W. H. & Wang, S. K. 2000 Side wall effects on the structure of laminar flow over a plane-symmetric sudden expansion. Comput. Fluids 29, 467–492.CrossRefGoogle Scholar
7. Drikakis, D. 1997 Bifurcation phenomena in incompressible sudden expansion flows. Phys. Fluids 9 (1).CrossRefGoogle Scholar
8. Durst, F., Melling, A. & Whitelaw, J. H. 1974 Low Reynolds number flow over a plane symmetric sudden expansion. J. Fluid Mech. 64 (1), 111–128.CrossRefGoogle Scholar
9. Durst, F., Pereira, J. C. F. & Tropea, C. 1993 The plane symmetric sudden-expansion flow at low Reynolds numbers. J. Fluid Mech. 249, 567–581.CrossRefGoogle Scholar
10. Fearn, R. M., Mullin, T. & Cliffe, K. A. 1990 Nonlinear flow phenomena in a symmetric sudden expansion. J. Fluid Mech. 211, 595–608.CrossRefGoogle Scholar
11. Hawa, T. & Rusak, Z. 2000 Viscous flow in a slightly asymmetric channel with a sudden expansion. Phys. Fluids 12 (9), 2257–2267.CrossRefGoogle Scholar
12. Hawa, T. & Rusak, Z. 2001 The dynamics of a laminar flow in a symmetric channel with a sudden expansion. J. Fluid Mech. 436, 283–320.CrossRefGoogle Scholar
13. Kuhlmann, H. C. 1999 Thermocapillary Convection in Models of Crystal Growth, Springer Tracts in Modern Physics , vol. 152. Springer.Google Scholar
14. Lanzerstorfer, D. & Kuhlmann, H. C. 2012a Global stability of the two-dimensional flow over a backward-facing step. J. Fluid Mech. 693, 1–27.CrossRefGoogle Scholar
15. Lanzerstorfer, D. & Kuhlmann, H. C. 2012b Three-dimensional instability of the flow over a forward-facing step. J. Fluid Mech. 695, 390–404.CrossRefGoogle Scholar
16. Lehoucq, R. B. & Sorensen, D. C. 1996 Deflation techniques for an implicitly restarted Arnoldi iteration. SIAM J. Matrix Anal. Appl. 17, 789–821.CrossRefGoogle Scholar
17. Mizushima, J. & Shiotani, Y. 2000 Structural instability of the bifurcation diagram for two-dimensional flow in a channel with a sudden expansion. J. Fluid Mech. 420, 131–145.CrossRefGoogle Scholar
18. Pierrehumbert, R. T. 1986 Universal short-wave instability of two-dimensional eddies in an inviscid fluid. Phys. Rev. Lett. 57, 2157–2159.CrossRefGoogle Scholar
19. Rusak, Z. & Hawa, T. 1999 A weakly nonlinear analysis of the dynamics of a viscous flow in a symmetric channel with a sudden expansion. Phys. Fluids 11 (12), 3629–3636.CrossRefGoogle Scholar
20. Schreck, E. & Schäfer, M. 2000 Numerical study of bifurcation in three-dimensional sudden channel expansions. Comput. Fluids 29 (5), 583–593.CrossRefGoogle Scholar
21. Shapira, M. & Degani, D. 1990 Stability and existence of multiple solutions for viscous flow in suddenly enlarged channels. Comput. Fluids 18 (3), 239–258.CrossRefGoogle Scholar
22. Shtern, V. & Hussain, F. 2003 Effect of deceleration on jet instability. J. Fluid Mech. 480, 283–309.CrossRefGoogle Scholar
23. Sipp, D. & Jacquin, L. 1998 Elliptic instability in two-dimensional flattened Taylor–Green vortices. Phys. Fluids 10, 839–849.CrossRefGoogle Scholar
24. Sipp, D. & Jacquin, L. 2000 Three-dimensional centrifugal-type instabilities of two-dimensional flows in rotating systems. Phys. Fluids 12, 1740–1748.CrossRefGoogle Scholar
25. Sobey, I. J. & Drazin, P. G. 1986 Bifurcations of two-dimensional channel flows. J. Fluid Mech. 171, 263–287.CrossRefGoogle Scholar
26. Squire, H. B. 1933 On the stability of three-dimensional disturbances of viscous flow between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.Google Scholar
27. Tsui, Y.-Y. & Wang, H.-W. 2008 Side-wall effects on the bifurcation of the flow through a sudden expansion. Intl J. Numer. Meth. Fluids 56, 167–184.CrossRefGoogle Scholar
28. Waleffe, F. 1990 On the three-dimensional instability of strained vortices. Phys. Fluids 2, 76–80.CrossRefGoogle Scholar