Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T09:04:58.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Gravity–capillary jet-like surface waves generated by an underwater bubble

Published online by Cambridge University Press:  18 March 2019

Youn J. Kang  and
Yeunwoo Cho Open the ORCID record for Yeunwoo Cho [Opens in a new window]
Youn J. Kang
Affiliation:
Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology, 291 Daehakro, Yuseonggu, Daejeon, 34141, Republic of Korea
Yeunwoo Cho*
Affiliation:
Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology, 291 Daehakro, Yuseonggu, Daejeon, 34141, Republic of Korea
*
†Email address for correspondence: ywoocho@kaist.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

Jet-like surface waves generated by an electric-spark-generated underwater bubble are experimentally studied. Three different motions of jet-like surface waves are observed depending on the inception position of the bubble (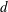$d$: 0.28–7 mm) below the free surface and the maximum radius of the bubble (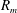$R_{m}$: 1.5–3.6 mm). When 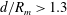$d/R_{m}>1.3$, the surface wave shows a simple smooth hump (case 1). When 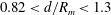$0.82<d/R_{m}<1.3$, a single droplet or multiple droplets are pinched off sequentially or simultaneously at the tip or from some points of the jet-like surface wave (case 2). Finally, when 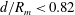$d/R_{m}<0.82$, a series of squirting and jetting phenomena are observed at the top of the jet-like surface wave (case 3). For case 1, a proportional relationship is found between 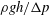$\unicode[STIX]{x1D70C}gh/\unicode[STIX]{x0394}p$ and 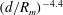$(d/R_{m})^{-4.4}$, where 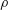$\unicode[STIX]{x1D70C}$ is the density of the fluid, 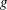$g$ is the gravitational acceleration and 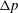$\unicode[STIX]{x0394}p$ is the difference between the reference atmospheric pressure and the vapour pressure inside a bubble. This proportional relationship is explained semi-analytically using a scaling argument and conservation of momentum and energy, with the help of the Kelvin impulse theory. In addition, we solve the relevant axisymmetric Cauchy–Poisson problem where the initial condition is a jet-like surface wave near its maximum height. By comparing the analytical wave solution with the observed surface wave pattern, it is found that the resultant surface waves are indeed gravity–capillary waves where both the gravity and the surface tension are equally important.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 841 - 864
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benjamin, T. B. & Ellis, A. T. 1966 The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries. Phil. Trans. R. Soc. Lond. A 260, 221–240.Google Scholar
Best, J. P. & Kucera, A. 1992 A numerical investigation of non-spherical rebounding bubbles. J. Fluid Mech. 245, 137–154.Google Scholar
Blake, J. R. & Cerone, P. 1982 A note on the impulse due to a vapour bubble near a boundary. J. Austral. Math Soc. B 23, 383–393.Google Scholar
Blake, J. R. & Gibson, D. C. 1981 Growth and collapse of a vapour cavity near a free surface. J. Fluid Mech. 111, 123–140.Google Scholar
Blake, J. R. & Gibson, D. C. 1987 Cavitation bubbles near boundaries. Annu. Rev. Fluid Mech. 19, 99–123.Google Scholar
Blake, J. R., Leppinen, D. M. & Wang, Q. 2015 Cavitation and bubble dynamics: the Kelvin impulse and its applications. Interface Focus 5, 20150017.Google Scholar
Brown, M. S., Kattamis, N. T. & Arnold, C. B. 2011 Implosion of an underwater spark-generated bubble and acoustic energy evaluation using the Rayleigh model. Microfluid Nanofluid 11, 199–207.Google Scholar
Buogo, S. & Cannelli, G. B. 2002 Implosion of an underwater spark-generated bubble and acoustic energy evaluation using the Rayleigh model. J. Acoust. Soc. Am. 111, 2594–2600.Google Scholar
Cerone, P. & Blake, J. R. 1984 A note on the instantaneous streamlines, pathlines and pressure contours for a cavitation bubble near a boundary. J. Austral. Math. Soc. Ser. B 26, 31–44.Google Scholar
Chahine, G. L. 1977 Interaction between an oscillating bubble and a free surface. Trans ASME J. Fluids Engng 99, 709–716.Google Scholar
Dadvand, A., Khoo, B. C. & Shervani-Tabar, M. T. 2009 A collapsing bubble-induced microinjector: an experimental study. Exp. Fluids 46, 419–434.Google Scholar
Dadvand, A., Shervani-Tabar, M. T. & Khoo, B. C. 2011 A note on spark bubble drop-on-demand droplet generation: simulation and experiment. Intl J. Adv. Manuf. Tech. 56, 245–259.Google Scholar
Debnath, L. 1994 Nonlinear Water Waves. Academic Press.Google Scholar
Du Noüy, P. L. 1925 An interfacial tensiometer for universal use. J. Gen. Physiol. 7, 625–631.Google Scholar
Duocastella, M., Fernández-Pradas, J. M., Morenza, J. L. & Serra, P. 2009 Time-resolved imaging of the laser forward transfer of liquids. J. Appl. Phys. 106, 084907.Google Scholar
Duocastella, M., Patrascioiu, A., Fernández-Pradas, J. M., Morenza, J. L. & Serra, P. 2009 Film-free laser forward printing of transparent and weakly absorbing liquids. Opt. Express. 18, 21815–21825.Google Scholar
Geers, T. L. & Hunter, K. S. 2002 An integrated wave-effects model for an underwater explosion bubble. J. Acoust. Soc. Am. 111, 1584–1601.Google Scholar
Gong, S. W., Ohl, S. W., Klaseboer, E. & Khoo, B. C. 2005 Scaling law for bubbles induced by different external sources: theoretical and experimental study. Phys. Rev. E 81, 056317.Google Scholar
Khoo, B. C., Klaseboer, E. & Hung, K. C. 2005 A collapsing bubble-induced micro-pump using the jetting effect. Sensors Actuators A 118, 152–161.Google Scholar
Klaseboer, E., Hung, K. C., Wang, C., Wang, C. W., Khoo, B. C., Boyce, P., Debono, S. & Charlier, H. 2005 Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure. J. Fluid Mech. 537, 387–413.Google Scholar
Lamb, H. 1993 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Lew, K. S. F., Klaseboer, E. & Khoo, B. C. 2007 A collapsing bubble-induced micropump: an experimental study. Sensors Actuators A 133, 161–172.Google Scholar
Miles, J. W. 1968 The Cauchy–Poisson problem for a viscous liquid. J. Fluid Mech. 34, 359–370.Google Scholar
Ohl, C. D., Arora, M., Dijkink, R., Janve, V. & Lohse, D. 2006 Surface cleaning from laser-induced cavitation bubbles. Appl. Phys. Lett. 89, 074102.Google Scholar
Pain, A., Hui Terence Goh, B., Klaseboer, E., Ohl, S. W. & Khoo, B. C. 2012 Jets in quiescent bubbles caused by a nearby oscillating bubble. J. Appl. Phys. 111, 054912.Google Scholar
Patrascioiu, A., Fernández-Pradas, J. M., Palla-Papavlu, A., Morenza, J. L. & Serra, P. 2014 Laser-generated liquid microjets: correlation between bubble dynamics and liquid ejection. Microfluid Nanofluid 16, 55–63.Google Scholar
Pearson, A., Cox, E., Blake, J. R. & Otto, S. R. 2004 Bubble interactions near a free surface. Engng Anal. Bound. Elem. 28, 295–313.Google Scholar
Plesset, M. S. & Chapman, R. B. 1971 Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary. J. Fluid Mech. 47, 283–290.Google Scholar
Rayleigh, L. 1917 On the pressure developed in a liquid during the collapse of a spherical cavity. Phil. Mag. 34, 94–98.Google Scholar
Reuter, F. & Mettin, R. 2016 Mechanisms of single bubble cleaning. Ultrason. Sonochem. 89, 550–562.Google Scholar
Robinson, P. B., Blake, J. R., Kodama, T., Shima, A. & Tomita, Y. 2001 Interaction of cavitation bubbles with a free surface. J. Appl. Phys. 89, 8225–8237.Google Scholar
Shervani-Tabar, M. T., Dadvand, A., Khoo, B. C. & Nobari, M. R. H. 2009 A numerical and experimental study of a collapsing bubble-induced droplet ejector. Theor. Comput. Fluid Dyn. 23, 297–316.Google Scholar
Stoker, J. J. 2011 Water Waves: The Mathematical Theory with Applications. Wiley.Google Scholar
Turangan, C. K., Ong, G. P., Klaseboer, E. & Khoo, B. C. 2006 Experimental and numerical study of transient bubble-elastic membrane interaction. J. Appl. Phys. 100, 054910.Google Scholar
Tomita, Y., Kodama, T. & Shima, A. 1991 Secondary cavitation due to interaction of a collapsing bubble with a rising free surface. Appl. Phys. Lett. 59, 274–276.Google Scholar
Wang, Q. X., Yeo, K. S., Khoo, B. C. & Lam, K. Y. 1996a Nonlinear interaction between gas bubble and free surface. Comput. Fluids 25, 607–628.Google Scholar
Wang, Q. X., Yeo, K. S., Khoo, B. C. & Lam, K. Y. 1996b Strong interaction between a buoyancy bubble and a free surface. Theor. Comput. Fluid Dyn. 8, 73–88.Google Scholar
Xiong, S., Chin, L. K., Ando, K., Tandiono, T., Liu, A. Q. & Ohl, C. D. 2015 Droplet generation via a single bubble transformation in a nanofluidic channel. Lab on a Chip 15, 1451–1457.Google Scholar
Zhang, S., Duncan, J. H. & Chahine, G. L. 1993 The final stage of the collapse of a cavitation bubble near a rigid wall. J. Fluid Mech. 257, 147–181.Google Scholar