Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-14T22:55:04.194Z Has data issue: false hasContentIssue false
  • English
  • Français

Grid criteria for numerical simulation of hypersonic aerothermodynamics in transition regime

Published online by Cambridge University Press:  24 October 2019

Xiang Ren Open the ORCID record for Xiang Ren [Opens in a new window] ,
Junya Yuan ,
Bijiao He ,
Mingxing Zhang  and
Guobiao Cai
Xiang Ren
Affiliation:
School of Astronautics, Beihang University, Beijing 100191, China
Junya Yuan
Affiliation:
School of Astronautics, Beihang University, Beijing 100191, China
Bijiao He
Affiliation:
School of Astronautics, Beihang University, Beijing 100191, China
Mingxing Zhang
Affiliation:
Beijing Institute of Space Long March Vehicle, Beijing 100076, China
Guobiao Cai*
Affiliation:
School of Astronautics, Beihang University, Beijing 100191, China
*
†Email address for correspondence: cgb@buaa.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Grid is an important factor in numerical simulation of hypersonic aerothermodynamics. This paper introduces three criteria for determining grid size in the transition flow regime when using the computational fluid dynamics (CFD) method or the direct simulation Monte Carlo (DSMC) method. The numerical relationship between these three criteria sizes is deduced according to the one-dimensional fluid theory. Then, the relationship is verified using the CFD method to simulate the flow around a two-dimensional cylinder. At the same time, the dependence of simulation accuracy on grid size in the CFD and DSMC methods is studied and the mechanism is given. The result shows that the simulation accuracy of heat flux especially depends on the normal grid size next to surfaces, where the 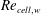$Re_{\mathit{cell},w}$ criterion and the 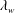$\unicode[STIX]{x1D706}_{w}$ criterion based on local parameters are applicable and equivalent, while the 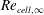$Re_{\mathit{cell},\infty }$ criterion based on the free-stream parameter is only applicable under the assumption of constant viscosity coefficient and constant temperature wall conditions. On the other hand, the trend of the heat flux changing with grid size obtained by CFD and DSMC is exactly the opposite. Therefore, the grid size must be strictly satisfied with the grid criteria when comparing CFD with DSMC and even the hybrid DSMC with Navier–Stokes method.

JFM classification

Aerodynamics: High-speed flow Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 585 - 601
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. D. Jr. 2010 Fundamentals of Aerodynamics. Tata McGraw-Hill Education.Google Scholar
Berger, A. E., Solomon, J. M., Ciment, M., Leventhal, S. H. & Weinberg, B. C. 1980 Generalized OCI schemes for boundary layer problems. Math. Comput. 35 (151), 695–731.Google Scholar
Bird, G. A.1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows. (Oxford Engineering Science Series, 42). Clarendon Press; Oxford University Press.Google Scholar
Bird, G. A. 2013 The DSMC Method. CreateSpace Independent Publishing Platform.Google Scholar
Brandis, A. M. & Johnston, C. O. 2014 Characterization of stagnation-point heat flux for earth entry. In 45th AIAA Plasmadynamics and Lasers Conference, p. 2374. AIAA.Google Scholar
Cercignani, C. 1988 The Boltzmann equation. In The Boltzmann Equation and Its Applications, pp. 40–103. Springer.Google Scholar
Ciment, M., Leventhal, S. H. & Weinberg, B. C. 1978 The operator compact implicit method for parabolic equations. J. Comput. Phys. 28 (2), 135–166.Google Scholar
Dilley, A. D. & McClinton, C. R.2001 Evaluation of CFD turbulent heating prediction techniques and comparison with hypersonic experimental data. NASA Tech. Rep. 2001–210837.Google Scholar
Fay, J. A. 1958 Theory of stagnation point heat transfer in dissociated air. J. Aerosp. Sci. 25 (2), 73–85.Google Scholar
Hoffmann, K., Siddiqui, M. & Chiang, S. 1991 Difficulties associated with the heat flux computations of high speed flows by the Navier–Stokes equations. In 29th Aerospace Sciences Meeting, p. 467.Google Scholar
Jasak, H.1996 Error analysis and estimation for the finite volume method with applications to fluid flows. PhD thesis, University of London Imperial College.Google Scholar
Kellogg, R., Shubin, G. & Stephens, A. 1980 Uniqueness and the cell Reynolds number. SIAM J. Numer. Anal. 17 (6), 733–739.Google Scholar
Klopfer, G. & Yee, H. 1988 Viscous hypersonic shock-on-shock interaction on blunt cowl lips. In 26th Aerospace Sciences Meeting, p. 233. AIAA.Google Scholar
Lofthouse, A. J., Scalabrin, L. C. & Boyd, I. D. 2008 Velocity slip and temperature jump in hypersonic aerothermodynamics. J. Thermophys. Heat Transfer 22, 38–49.Google Scholar
Maxwell, J. C. III 1878 On stresses in rarefied gases arising from inequalities of temperature. Proc. R. Soc. Lond. 27 (185–189), 304–308.Google Scholar
Men’shov, I. S. & Nakamura, Y. 2000 Numerical simulations and experimental comparisons for high-speed nonequilibrium air flows. Fluid Dyn. Res. 27 (5), 305–334.Google Scholar
Myong, R. S. 2011 Impact of computational physics on multi-scale CFD and related numerical algorithms. Comput. Fluids 45 (1), 64–69.Google Scholar
Papadopoulos, P., Venkatapathy, E., Prabhu, D., Loomis, M. P. & Olynick, D. 1999 Current grid-generation strategies and future requirements in hypersonic vehicle design, analysis and testing. Appl. Math. Modell. 23 (9), 705–735.Google Scholar
Scanlon, T. J., Roohi, E., White, C., Darbandi, M. & Reese, J. M. 2010 An open source, parallel DSMC code for rarefied gas flows in arbitrary geometries. Comput. Fluids 39 (10), 2078–2089.Google Scholar
Siddiqui, M. S., Hoffmann, K. A., Chiang, S. T. & Rutledge, W. H. 1992 A comparative study of the Navier Stokes solvers with emphasis on the heat transfer computations of high speed flows. In 30th Aerospace Sciences Meeting and Exhibit. AIAA.Google Scholar
Singh, N. & Schwartzentruber, T. E. 2016 Heat flux correlation for high-speed flow in the transitional regime. J. Fluid Mech. 792, 981–996.Google Scholar
Singh, N. & Schwartzentruber, T. E. 2017 Aerothermodynamic correlations for high-speed flow. J. Fluid Mech. 821, 421–439.Google Scholar
Smoluchowski von Smolan, M. 1898 Über Wärmeleitung in verdünnten Gasen. Ann. Phys. 300 (1), 101–130.Google Scholar
Sutton, K. & Graves, R. A. Jr. 1971 A general stagnation-point convective heating equation for arbitrary gas mixtures. NASA Tech. Rep. R-376t.Google Scholar
Tsien, H. S. 1946 Superaerodynamics, mechanics of rarefied gases. J. Aeronaut. Sci. 13 (12), 653–664.Google Scholar
Xiang, Z., Wei, Y. & Haibo, H. 2017 Computational grid dependency in CFD simulation for heat transfer. In 2017 8th International Conference on Mechanical and Aerospace Engineering (ICMAE), pp. 193–197. IEEE.Google Scholar
Yang, J. & Liu, M. 2017 A wall grid scale criterion for hypersonic aerodynamic heating calculation. Acta Astron. 136, 137–143.Google Scholar
Zel’Dovich, Y. B. & Raizer, Y. P. 2012 Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. Courier Corporation.Google Scholar