Article contents
Heat transfer in rotating Rayleigh–Bénard convection with rough plates
Published online by Cambridge University Press: 03 October 2017
Abstract
This experimental study focuses on the effect of horizontal boundaries with pyramid-shaped roughness elements on the heat transfer in rotating Rayleigh–Bénard convection. It is shown that the Ekman pumping mechanism, which is responsible for the heat transfer enhancement under rotation in the case of smooth top and bottom surfaces, is unaffected by the roughness as long as the Ekman layer thickness 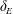 $\unicode[STIX]{x1D6FF}_{E}$ is significantly larger than the roughness height
$\unicode[STIX]{x1D6FF}_{E}$ is significantly larger than the roughness height 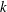 $k$. As the rotation rate increases, and thus
$k$. As the rotation rate increases, and thus  $\unicode[STIX]{x1D6FF}_{E}$ decreases, the roughness elements penetrate the radially inward flow in the interior of the Ekman boundary layer that feeds the columnar Ekman vortices. This perturbation generates additional thermal disturbances which are found to increase the heat transfer efficiency even further. However, when
$\unicode[STIX]{x1D6FF}_{E}$ decreases, the roughness elements penetrate the radially inward flow in the interior of the Ekman boundary layer that feeds the columnar Ekman vortices. This perturbation generates additional thermal disturbances which are found to increase the heat transfer efficiency even further. However, when 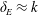 $\unicode[STIX]{x1D6FF}_{E}\approx k$, the Ekman boundary layer is strongly perturbed by the roughness elements and the Ekman pumping mechanism is suppressed. The results suggest that the Ekman pumping is re-established for
$\unicode[STIX]{x1D6FF}_{E}\approx k$, the Ekman boundary layer is strongly perturbed by the roughness elements and the Ekman pumping mechanism is suppressed. The results suggest that the Ekman pumping is re-established for 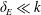 $\unicode[STIX]{x1D6FF}_{E}\ll k$ as the faces of the pyramidal roughness elements then act locally as a sloping boundary on which an Ekman layer can be formed.
$\unicode[STIX]{x1D6FF}_{E}\ll k$ as the faces of the pyramidal roughness elements then act locally as a sloping boundary on which an Ekman layer can be formed.
- Type
- Rapids
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 10
- Cited by



