Published online by Cambridge University Press: 26 August 2014
Helicity, which is defined as the scalar product of velocity and vorticity, 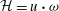 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathcal{H}} = {\boldsymbol {u}} \boldsymbol {\cdot }\boldsymbol{\omega}$, is an inviscidly conserved quantity in a barotropic fluid. Mean helicity is zero in flows that are parity invariant. System rotation breaks parity invariance and has therefore the potential of giving rise to non-zero mean helicity. In this paper we study the helicity dynamics in the incompressible Ekman boundary layer. Evolution equations for the mean field helicity and the mean turbulent helicity are derived and it is shown that pressure flux injects helicity at a rate
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathcal{H}} = {\boldsymbol {u}} \boldsymbol {\cdot }\boldsymbol{\omega}$, is an inviscidly conserved quantity in a barotropic fluid. Mean helicity is zero in flows that are parity invariant. System rotation breaks parity invariance and has therefore the potential of giving rise to non-zero mean helicity. In this paper we study the helicity dynamics in the incompressible Ekman boundary layer. Evolution equations for the mean field helicity and the mean turbulent helicity are derived and it is shown that pressure flux injects helicity at a rate 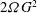 $ 2 \varOmega G^2 $ over the total depth of the Ekman layer, where
$ 2 \varOmega G^2 $ over the total depth of the Ekman layer, where 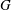 $ G $ is the geostrophic wind far from the wall and
$ G $ is the geostrophic wind far from the wall and 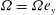 $ {\boldsymbol{\Omega}} = \varOmega {\boldsymbol {e}}_y $ is the rotation vector and
$ {\boldsymbol{\Omega}} = \varOmega {\boldsymbol {e}}_y $ is the rotation vector and 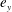 $ {\boldsymbol {e}}_y $ is the wall-normal unit vector. Thus right-handed/left-handed helicity will be injected if
$ {\boldsymbol {e}}_y $ is the wall-normal unit vector. Thus right-handed/left-handed helicity will be injected if 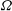 $ \varOmega $ is positive/negative. We also show that in the uppermost part of the boundary layer there is a net helicity injection with opposite sign as compared with the totally integrated injection. Isotropic relations for the helicity dissipation and the helicity spectrum are derived and it is shown that it is sufficient to measure two transverse velocity components and use Taylor’s hypothesis in the mean flow direction in order to measure the isotropic helicity spectrum. We compare the theoretical predictions with a direct numerical simulation of an Ekman boundary layer and confirm that there is a preference for right-handed helicity in the lower part of the Ekman layer and left-handed helicity in the uppermost part when
$ \varOmega $ is positive/negative. We also show that in the uppermost part of the boundary layer there is a net helicity injection with opposite sign as compared with the totally integrated injection. Isotropic relations for the helicity dissipation and the helicity spectrum are derived and it is shown that it is sufficient to measure two transverse velocity components and use Taylor’s hypothesis in the mean flow direction in order to measure the isotropic helicity spectrum. We compare the theoretical predictions with a direct numerical simulation of an Ekman boundary layer and confirm that there is a preference for right-handed helicity in the lower part of the Ekman layer and left-handed helicity in the uppermost part when 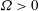 $ \varOmega > 0 $. In the logarithmic range, the helicity dissipation conforms to isotropic relations. On the other hand, spectra show significant departures from isotropic conditions, suggesting that the Reynolds number considered in the study is not sufficiently large for isotropy to be valid in a wide range of scales. Our analytical and numerical results strongly suggest that there is a turbulent helicity cascade of right-handed helicity in the logarithmic range of the atmospheric boundary layer when
$ \varOmega > 0 $. In the logarithmic range, the helicity dissipation conforms to isotropic relations. On the other hand, spectra show significant departures from isotropic conditions, suggesting that the Reynolds number considered in the study is not sufficiently large for isotropy to be valid in a wide range of scales. Our analytical and numerical results strongly suggest that there is a turbulent helicity cascade of right-handed helicity in the logarithmic range of the atmospheric boundary layer when 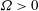 $\varOmega >0$, consistent with recent measurements by Koprov, Koprov, Ponomarev & Chkhetiani (Dokl. Phys., vol. 50, 2005, pp. 419–422). The isotropic relations which are derived may facilitate future measurements of the helicity spectrum in the atmospheric boundary layer as well as in controlled wind tunnel experiments.
$\varOmega >0$, consistent with recent measurements by Koprov, Koprov, Ponomarev & Chkhetiani (Dokl. Phys., vol. 50, 2005, pp. 419–422). The isotropic relations which are derived may facilitate future measurements of the helicity spectrum in the atmospheric boundary layer as well as in controlled wind tunnel experiments.