Article contents
A hierarchical random additive model for passive scalars in wall-bounded flows at high Reynolds numbers
Published online by Cambridge University Press: 09 March 2018
Abstract
The kinematics of a fully developed passive scalar is modelled using the hierarchical random additive process (HRAP) formalism. Here, ‘a fully developed passive scalar’ refers to a scalar field whose instantaneous fluctuations are statistically stationary, and the ‘HRAP formalism’ is a recently proposed interpretation of the Townsend attached eddy hypothesis. The HRAP model was previously used to model the kinematics of velocity fluctuations in wall turbulence: 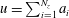 $u=\sum _{i=1}^{N_{z}}a_{i}$, where the instantaneous streamwise velocity fluctuation at a generic wall-normal location
$u=\sum _{i=1}^{N_{z}}a_{i}$, where the instantaneous streamwise velocity fluctuation at a generic wall-normal location  $z$ is modelled as a sum of additive contributions from wall-attached eddies (
$z$ is modelled as a sum of additive contributions from wall-attached eddies (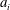 $a_{i}$) and the number of addends is
$a_{i}$) and the number of addends is 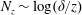 $N_{z}\sim \log (\unicode[STIX]{x1D6FF}/z)$. The HRAP model admits generalized logarithmic scalings including
$N_{z}\sim \log (\unicode[STIX]{x1D6FF}/z)$. The HRAP model admits generalized logarithmic scalings including 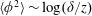 $\langle \unicode[STIX]{x1D719}^{2}\rangle \sim \log (\unicode[STIX]{x1D6FF}/z)$,
$\langle \unicode[STIX]{x1D719}^{2}\rangle \sim \log (\unicode[STIX]{x1D6FF}/z)$, 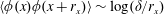 $\langle \unicode[STIX]{x1D719}(x)\unicode[STIX]{x1D719}(x+r_{x})\rangle \sim \log (\unicode[STIX]{x1D6FF}/r_{x})$,
$\langle \unicode[STIX]{x1D719}(x)\unicode[STIX]{x1D719}(x+r_{x})\rangle \sim \log (\unicode[STIX]{x1D6FF}/r_{x})$, 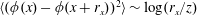 $\langle (\unicode[STIX]{x1D719}(x)-\unicode[STIX]{x1D719}(x+r_{x}))^{2}\rangle \sim \log (r_{x}/z)$, where
$\langle (\unicode[STIX]{x1D719}(x)-\unicode[STIX]{x1D719}(x+r_{x}))^{2}\rangle \sim \log (r_{x}/z)$, where 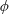 $\unicode[STIX]{x1D719}$ is the streamwise velocity fluctuation,
$\unicode[STIX]{x1D719}$ is the streamwise velocity fluctuation, 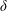 $\unicode[STIX]{x1D6FF}$ is an outer length scale,
$\unicode[STIX]{x1D6FF}$ is an outer length scale, 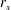 $r_{x}$ is the two-point displacement in the streamwise direction and
$r_{x}$ is the two-point displacement in the streamwise direction and 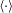 $\langle \cdot \rangle$ denotes ensemble averaging. If the statistical behaviours of the streamwise velocity fluctuation and the fluctuation of a passive scalar are similar, we can expect first that the above mentioned scalings also exist for passive scalars (i.e. for
$\langle \cdot \rangle$ denotes ensemble averaging. If the statistical behaviours of the streamwise velocity fluctuation and the fluctuation of a passive scalar are similar, we can expect first that the above mentioned scalings also exist for passive scalars (i.e. for 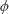 $\unicode[STIX]{x1D719}$ being fluctuations of scalar concentration) and second that the instantaneous fluctuations of a passive scalar can be modelled using the HRAP model as well. Such expectations are confirmed using large-eddy simulations. Hence the work here presents a framework for modelling scalar turbulence in high Reynolds number wall-bounded flows.
$\unicode[STIX]{x1D719}$ being fluctuations of scalar concentration) and second that the instantaneous fluctuations of a passive scalar can be modelled using the HRAP model as well. Such expectations are confirmed using large-eddy simulations. Hence the work here presents a framework for modelling scalar turbulence in high Reynolds number wall-bounded flows.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 37
- Cited by



