Published online by Cambridge University Press: 30 June 2016
It is shown that the formal expression for the effective viscosity of a dilute suspension of arbitrary-shaped particles in Poiseuille flow contains a novel quadrupole term, besides the expected stresslet. This term becomes important for a very confined geometry. For a high-frequency flow field (in the sense used in Feuillebois et al. (J. Fluid Mech., vol. 764, 2015, pp. 133–147), the suspension rheology is Newtonian at first order in volume fraction. The effective viscosity is calculated for suspensions of 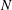 $N$-bead rods and of prolate spheroids with the same length, volume and aspect ratio (up to 6), entrained by the Poiseuille flow between two infinite parallel flat hard walls. The numerical computations, based on solving the Stokes equations, indicate that the quadrupole term gives a significant positive contribution to the intrinsic viscosity
$N$-bead rods and of prolate spheroids with the same length, volume and aspect ratio (up to 6), entrained by the Poiseuille flow between two infinite parallel flat hard walls. The numerical computations, based on solving the Stokes equations, indicate that the quadrupole term gives a significant positive contribution to the intrinsic viscosity 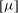 $[{\it\mu}]$ if the distance between the walls is less than ten times the particle width, or less. It is found that the intrinsic viscosity in bounded Poiseuille flow is generally smaller than the corresponding value in unbounded flow, except for extremely narrow gaps when it becomes larger because of lubrication effects. The intrinsic viscosity is at a minimum for a gap between walls of the order of 1.5–2 particle width. For spheroids, the intrinsic viscosity is generally smaller than for chains of beads with the same aspect ratio, but when normalized by its value in the bulk, the results are qualitatively the same. Therefore, a rigid chain of beads can serve as a simple model of an orthotropic particle with a more complicated shape. The important conclusion is that the intrinsic viscosity in shear flow is larger than in the Poiseuille flow between two walls, and the difference is significant even for relatively wide channels, e.g. three times wider than the particle length. For such confined geometries, the hydrodynamic interactions with the walls are significant and should be taken into account.
$[{\it\mu}]$ if the distance between the walls is less than ten times the particle width, or less. It is found that the intrinsic viscosity in bounded Poiseuille flow is generally smaller than the corresponding value in unbounded flow, except for extremely narrow gaps when it becomes larger because of lubrication effects. The intrinsic viscosity is at a minimum for a gap between walls of the order of 1.5–2 particle width. For spheroids, the intrinsic viscosity is generally smaller than for chains of beads with the same aspect ratio, but when normalized by its value in the bulk, the results are qualitatively the same. Therefore, a rigid chain of beads can serve as a simple model of an orthotropic particle with a more complicated shape. The important conclusion is that the intrinsic viscosity in shear flow is larger than in the Poiseuille flow between two walls, and the difference is significant even for relatively wide channels, e.g. three times wider than the particle length. For such confined geometries, the hydrodynamic interactions with the walls are significant and should be taken into account.