Article contents
High-frequency viscosity of a dilute suspension of elongated particles in a linear shear flow between two walls
Published online by Cambridge University Press: 23 December 2014
Abstract
A general expression for the effective viscosity of a dilute suspension of arbitrary-shaped particles in linear shear flow between two parallel walls is derived in terms of the induced stresslets on particles. This formula is applied to 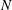 $N$ -bead rods and to prolate spheroids with the same length, aspect ratio and volume. The effective viscosity of non-Brownian particles in a periodic shear flow is considered here. The oscillating frequency is high enough for the particle orientation and centre-of-mass distribution to be practically frozen, yet small enough for the flow to be quasi-steady. It is known that for spheres, the intrinsic viscosity
$N$ -bead rods and to prolate spheroids with the same length, aspect ratio and volume. The effective viscosity of non-Brownian particles in a periodic shear flow is considered here. The oscillating frequency is high enough for the particle orientation and centre-of-mass distribution to be practically frozen, yet small enough for the flow to be quasi-steady. It is known that for spheres, the intrinsic viscosity 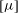 $[{\it\mu}]$ increases monotonically when the distance
$[{\it\mu}]$ increases monotonically when the distance 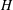 $H$ between the walls is decreased. The dependence is more complex for both types of elongated particles. Three regimes are theoretically predicted here: (i) a ‘weakly confined’ regime (for
$H$ between the walls is decreased. The dependence is more complex for both types of elongated particles. Three regimes are theoretically predicted here: (i) a ‘weakly confined’ regime (for 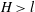 $H>l$ , where
$H>l$ , where 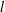 $l$ is the particle length), where
$l$ is the particle length), where 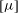 $[{\it\mu}]$ is slightly larger for smaller
$[{\it\mu}]$ is slightly larger for smaller 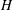 $H$ ; (ii) a ‘semi-confined’ regime, when
$H$ ; (ii) a ‘semi-confined’ regime, when  $H$ becomes smaller than
$H$ becomes smaller than 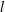 $l$ , where
$l$ , where 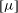 $[{\it\mu}]$ rapidly decreases since the geometric constraints eliminate particle orientations corresponding to the largest stresslets; (iii) a ‘strongly confined’ regime when
$[{\it\mu}]$ rapidly decreases since the geometric constraints eliminate particle orientations corresponding to the largest stresslets; (iii) a ‘strongly confined’ regime when 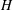 $H$ becomes smaller than 2–3 particle widths
$H$ becomes smaller than 2–3 particle widths 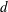 $d$ , where
$d$ , where 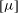 $[{\it\mu}]$ rapidly increases owing to the strong hydrodynamic coupling with the walls. In addition, for sufficiently slender particles (with aspect ratio larger than 5–6) there is a domain of narrow gaps for which the intrinsic viscosity is smaller than that in unbounded fluid.
$[{\it\mu}]$ rapidly increases owing to the strong hydrodynamic coupling with the walls. In addition, for sufficiently slender particles (with aspect ratio larger than 5–6) there is a domain of narrow gaps for which the intrinsic viscosity is smaller than that in unbounded fluid.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 5
- Cited by


