Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Breakey, David E. S.
Jordan, Peter
Cavalieri, André V. G.
Nogueira, Petrônio A.
Léon, Olivier
Colonius, Tim
and
Rodríguez, Daniel
2017.
Experimental study of turbulent-jet wave packets and their acoustic efficiency.
Physical Review Fluids,
Vol. 2,
Issue. 12,
Mancinelli, Matteo
and
Camussi, Roberto
2018.
Acceleration and wall pressure fluctuations generated by an incompressible jet in installed configuration
.
Comptes Rendus. Mécanique,
Vol. 346,
Issue. 10,
p.
919.
Ormonde, Pedro C.
Cavalieri, André V. G.
Silva, Roberto G. A. da
and
Avelar, Ana C.
2018.
Passive control of coherent structures in a modified backwards-facing step flow.
Experiments in Fluids,
Vol. 59,
Issue. 5,
Schmidt, Oliver T.
Towne, Aaron
Rigas, Georgios
Colonius, Tim
and
Brès, Guillaume A.
2018.
Spectral analysis of jet turbulence.
Journal of Fluid Mechanics,
Vol. 855,
Issue. ,
p.
953.
Lesshafft, Lutz
Jordan, Peter
and
Agarwal, Anurag
2018.
Foreword.
Comptes Rendus. Mécanique,
Vol. 346,
Issue. 10,
p.
887.
Brès, Guillaume A.
Jordan, Peter
Jaunet, Vincent
Le Rallic, Maxime
Cavalieri, André V. G.
Towne, Aaron
Lele, Sanjiva K.
Colonius, Tim
and
Schmidt, Oliver T.
2018.
Importance of the nozzle-exit boundary-layer state in subsonic turbulent jets.
Journal of Fluid Mechanics,
Vol. 851,
Issue. ,
p.
83.
Wong, Marcus H.
Edgington-Mitchell, Daniel M.
Honnery, Damon R.
Jordan, Peter
and
Savarese, Alessandro
2018.
Kinematic wavepacket model for broadband shock associated noise in underexpanded supersonic jets.
Cavalieri, André V. G.
Jordan, Peter
and
Lesshafft, Lutz
2019.
Wave-Packet Models for Jet Dynamics and Sound Radiation.
Applied Mechanics Reviews,
Vol. 71,
Issue. 2,
Pickering, Ethan M.
Rigas, Georgios
Sipp, Denis
Schmidt, Oliver T.
and
Colonius, Tim
2019.
Eddy viscosity for resolvent-based jet noise models.
Wong, Marcus H.
Jordan, Peter
Honnery, Damon R.
and
Edgington-Mitchell, Daniel
2019.
Impact of coherence decay on wavepacket models for broadband shock-associated noise in supersonic jets.
Journal of Fluid Mechanics,
Vol. 863,
Issue. ,
p.
969.
Neilsen, Tracianne B.
Vaughn, Aaron B.
Gee, Kent L.
Akamine, Masahito
Okamoto, Koji
Teramoto, Susumu
and
Tsutsumi, Seiji
2019.
Data-educed broadband equivalent acoustic source model for supersonic jet noise.
The Journal of the Acoustical Society of America,
Vol. 146,
Issue. 5,
p.
3409.
Wong, Marcus H.
Edgington-Mitchell, Daniel M.
Honnery, Damon
Cavalieri, André V.
and
Jordan, Peter
2019.
A Parabolised Stability Equation based Broadband Shock-Associated Noise Model.
Edgington-Mitchell, Daniel
2019.
Aeroacoustic resonance and self-excitation in screeching and impinging supersonic jets – A review.
International Journal of Aeroacoustics,
Vol. 18,
Issue. 2-3,
p.
118.
Soares, Luiz F. M.
Cavalieri, André V. G.
Kopiev, Victor
and
Faranosov, Georgy
2020.
Flight Effects on Turbulent-Jet Wave Packets.
AIAA Journal,
Vol. 58,
Issue. 9,
p.
3877.
Chakrabarti, Surya
Gaitonde, Datta V.
and
Unnikrishnan, Sasidharan
2020.
The Dynamics of Azimuthal Modes in Rectangular Jets.
Zhang, Zhongyu
and
Wu, Xuesong
2020.
Nonlinear evolution and acoustic radiation of coherent structures in subsonic turbulent free shear layers.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Martini, Eduardo
Cavalieri, André V. G.
Jordan, Peter
Towne, Aaron
and
Lesshafft, Lutz
2020.
Resolvent-based optimal estimation of transitional and turbulent flows.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Unnikrishnan, S.
and
Gaitonde, Datta V.
2020.
A pressure decomposition framework for aeroacoustic analysis of turbulent jets.
European Journal of Mechanics - B/Fluids,
Vol. 81,
Issue. ,
p.
41.
Wong, Marcus H.
Kirby, Rhiannon
Jordan, Peter
and
Edgington-Mitchell, Daniel
2020.
Azimuthal decomposition of the radiated noise from supersonic shock-containing jets.
The Journal of the Acoustical Society of America,
Vol. 148,
Issue. 4,
p.
2015.
Kuhn, Phoebe
Soria, Julio
and
Oberleithner, Kilian
2021.
Linear modelling of self-similar jet turbulence.
Journal of Fluid Mechanics,
Vol. 919,
Issue. ,
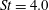 $St=4.0$ and azimuthal wavenumber
$St=4.0$ and azimuthal wavenumber 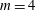 $m=4$ by comparing solutions of the parabolised stability equations with a well-validated large-eddy simulation of a Mach 0.9 turbulent jet. The results show that the near-nozzle dynamics can be correctly described by the homogeneous linear model, the initial growth rates being accurately predicted for the entire range of frequencies and azimuthal wavenumbers considered. Similarly to the lower-frequency wavepackets reported prior to this work, the high-frequency linear waves deviate from the data downstream of their stabilisation locations, which move progressively upstream as the frequency increases.
$m=4$ by comparing solutions of the parabolised stability equations with a well-validated large-eddy simulation of a Mach 0.9 turbulent jet. The results show that the near-nozzle dynamics can be correctly described by the homogeneous linear model, the initial growth rates being accurately predicted for the entire range of frequencies and azimuthal wavenumbers considered. Similarly to the lower-frequency wavepackets reported prior to this work, the high-frequency linear waves deviate from the data downstream of their stabilisation locations, which move progressively upstream as the frequency increases.


