Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-30T22:55:32.217Z Has data issue: false hasContentIssue false
  • English
  • Français

High-Strouhal-number pulsatile flow in a curved pipe

Published online by Cambridge University Press:  27 July 2021

Feroz Ahmed Open the ORCID record for Feroz Ahmed [Opens in a new window] ,
Ian Eames Open the ORCID record for Ian Eames [Opens in a new window] ,
Emad Moeendarbary  and
Alireza Azarbadegan
Feroz Ahmed*
Affiliation:
Centre for Engineering in Extreme Environments, University College London, Torrington Place, LondonWC1E 7JE, UK
Ian Eames
Affiliation:
Centre for Engineering in Extreme Environments, University College London, Torrington Place, LondonWC1E 7JE, UK
Emad Moeendarbary
Affiliation:
Mechanics in Biology & Medicine Group (MecBioMed), Department of Mechanical Engineering, University College London, Torrington Place, LondonWC1E 7JE, UK
Alireza Azarbadegan
Affiliation:
BP Exploration Operating Company Limited, Chertsey Road, Sunbury-on-Thames, MiddlesexTW16 7NL, UK
*
†Email address for correspondence: ucemfah@ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

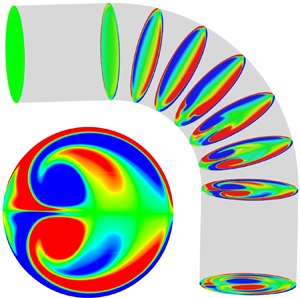
The high-Strouhal-number pulsatile flow in a curved pipe is studied numerically. A general force analysis is developed for the bend force, where the new contribution from flow acceleration is identified and analysed. The mechanisms of secondary flow production are studied by extending Hawthorne's (Proc. R. Soc. Lond. A, vol. 206, issue 1086, 1951, pp. 374–387) model to account for viscous effects and applied to assess the distinct contributions from an inviscid stretching and no-slip condition. A detailed comparison is made between the numerical simulations and models for a pipe flow characterised by a volume flux $Q=U_b A |\sin \varOmega _p t|$ (where $U_b$ is the maximum bulk velocity, $\varOmega _p$ is the angular frequency and $A$ is the pipe cross-sectional area). For high-Reynolds-number ($Re_b$) and high-Strouhal-number ($St$), the bend force predictions are in good agreement with the numerical results over a wide range of bend curvature ($R_c/D$; where $R_c$ is the bend radius of curvature and $D$ is the pipe diameter) owing to the influence of the streamwise flow acceleration on the pressure field. At high-$St$, the streamwise vorticity (secondary flow) distribution is steady and close to the low-$St$ case, which is explained using a linear secondary flow model.

JFM classification

Boundary Layers: Pipe flow boundary layer Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 923 , 25 September 2021 , A15
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

API-688 2012 Pulsation and vibration control in positive displacement machinery systems for petroleum, petrochemical, and natural gas industry services. A. Petrol. Inst. 1, 1–128.Google Scholar
Bertelsen, A.F. 1975 An experimental investigation of low Reynolds number secondary streaming effects associated with an oscillating viscous flow in a curved pipe. J. Fluid Mech. 70, 519–527.CrossRefGoogle Scholar
Boiron, O., Deplano, V. & Pelissier, R. 2007 Experimental and numerical studies on the starting effect on the secondary flow in a bend. J. Fluid Mech. 574, 109–129.CrossRefGoogle Scholar
Cox, C., Najjari, M.R. & Plesniak, M.W. 2019 Three-dimensional vortical structures and wall shear stress in a curved artery model. Phys. Fluids 31 (12), 121903.CrossRefGoogle Scholar
Das, D. & Arakeri, J.H. 1998 Transition of unsteady velocity profiles with reverse flow. J. Fluid Mech. 374, 251–283.CrossRefGoogle Scholar
Das, D. & Arakeri, J.H. 2000 Unsteady laminar duct flow with a given volume flow rate variation. J. Appl. Mech. 67 (2), 274–281.CrossRefGoogle Scholar
Das, S.P., Srinivasan, U. & Arakeri, J.H. 2016 Instabilities in unsteady boundary layers with reverse flow. Eur. J. Mech. (B/Fluids) 55, 49–62.CrossRefGoogle Scholar
Dean, W.R. 1927 XVI. Note on the motion of fluid in a curved pipe. Lond. Edinb. Dublin Phil. Mag. J. Sci. 4 (20), 208–223.CrossRefGoogle Scholar
Dean, W.R. 1928 LXXII. The stream-line motion of fluid in a curved pipe. Lond. Edinb. Dublin Phil. Mag. J. Sci. 5 (30), 673–695.CrossRefGoogle Scholar
EI 2008 Guidelines for the avoidance of vibration induced fatigue failure in process pipe work. Energy Institute 2, 1–226.Google Scholar
Einstein, A. 1926 The cause of the formation of meanders in the courses of rivers and of the so-called Baer's law. Naturwissenschaften 14, 223–224.CrossRefGoogle Scholar
Haddad, K., Ertunç, Ö., Mishra, M. & Delgado, A. 2010 Pulsating laminar fully developed channel and pipe flows. Phys. Rev. E 81 (1), 016303.CrossRefGoogle ScholarPubMed
Hawthorne, W.R. 1951 Secondary circulation in fluid flow. Proc. R. Soc. Lond. A 206 (1086), 374–387.Google Scholar
Hellstrom, F. & Fuchs, L. 2007 Numerical computations of steady and unsteady flow in bended pipes. In 37th AIAA Fluid Dynamics Conference.CrossRefGoogle Scholar
Hou, D.Q., Tijsseling, A.S. & Bozkus, Z. 2014 Dynamic force on an elbow caused by a traveling liquid slug. Trans. ASME: J. Press. Vessel Technol. 136 (3), 031302.Google Scholar
Hunt, J.C.R. 1973 A theory of turbulent flow round two-dimensional bluff bodies. J. Fluid Mech. 61, 625–706.CrossRefGoogle Scholar
Hunt, J.C.R., Abell, C.J., Peterka, J.A. & Woo, H. 1978 Kinematical studies of the flows around free or surface-mounted obstacles; applying topology to flow visualization. J. Fluid Mech. 86 (1), 179–200.CrossRefGoogle Scholar
Hunt, J.C.R., Wray, A.A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proceedings Summer Program. Center for Turbulence Research Report CTR-S88, pp. 193–208.Google Scholar
Inthavong, K. 2019 A unifying correlation for laminar particle deposition in 90-degree pipe bends. Powder Technol. 345, 99–110.CrossRefGoogle Scholar
Jarrahi, M., Castelain, C. & Peerhossaini, H. 2011 Secondary flow patterns and mixing in laminar pulsating flow through a curved pipe. Exp. Fluids 50 (6), 1539–1558.CrossRefGoogle Scholar
Kalpakli, A., Örlü, R., Tillmark, N. & Alfredsson, P.H. 2010 Experimental investigation on the effect of pulsations on turbulent flow through a 90 degrees pipe bend. In Proceedings 3rd International Conference on Jets, Wakes and Separated Flows, Cincinnati, Ohio, USA.Google Scholar
Kartik, V.B. & Michael, W.P. 2018 Insights on arterial secondary flow structures and vortex dynamics gained using the MRV technique. Intl J. Heat Fluid Flow 73, 143–153.Google Scholar
Komai, Y. & Tanishita, K. 1997 Fully developed intermittent flow in a curved tube. J. Fluid Mech. 347, 263–287.CrossRefGoogle Scholar
Krishna, C.V., Gundiah, N. & Arakeri, J.H. 2017 Separations and secondary structures due to unsteady flow in a curved pipe. J. Fluid Mech. 815, 26–59.CrossRefGoogle Scholar
Lighthill, M.J. 1956 Drift. J. Fluid Mech. 1, 31–53.CrossRefGoogle Scholar
Lyne, W.H. 1971 Unsteady viscous flow in a curved pipe. J. Fluid Mech. 45, 13–32.CrossRefGoogle Scholar
Mahmoudi Zarandi, M. 2000 Steady and pulsatile flow in curved vessels. PhD thesis, California Institute of Technology, CA.Google Scholar
Manring, N.D. 2000 The discharge flow ripple of an axial-piston swash-plate type hydrostatic pump. Trans. ASME: J. Dyn. Syst. 122, 263–268.CrossRefGoogle Scholar
Miller, J.E. 1987 The Reciprocating Pump: Theory, Design, and Use. John Wiley & Sons.Google Scholar
Miller, J.E. 1988 Characteristics of the reciprocating pump. In Proceedings 5th International Pump Users Symposium, pp. 163–174.Google Scholar
Muntges, D. & Majdalani, J. 2002 Pulsatory channel flow for an arbitrary volumetric flowrate. In 32nd AIAA Fluid Dynamics Conference Exhibitions, p. 2856.Google Scholar
Najjari, M.R., Cox, C. & Plesniak, M. 2019 Formation and interaction of multiple secondary flow vortical structures in a curved pipe: transient and oscillatory flows. J. Fluid Mech. 876, 481–526.CrossRefGoogle Scholar
Najjari, M.R. & Plesniak, M.W. 2016 Evolution of vortical structures in a curved artery model with non-newtonian blood-analog fluid under pulsatile inflow conditions. Exp. Fluids 57 (6), 1–16.CrossRefGoogle Scholar
Najjari, M.R. & Plesniak, M.W. 2018 Secondary flow vortical structures in a $180^{\circ }$ elastic curved vessel with torsion under steady and pulsatile inflow conditions. Phys. Rev. Fluids 3 (01), 013101.CrossRefGoogle Scholar
Olson, D.E. & Snyder, B. 1985 The upstream scale of flow development in curved circular pipes. J. Fluid Mech. 150, 139–158.CrossRefGoogle Scholar
Plesniak, M. & Bulusu, K. 2016 Morphology of secondary flows in a curved pipe with pulsatile inflow. Trans. ASME J. Fluids Engng 138 (10), 101203.CrossRefGoogle Scholar
Potter, M.C., Wiggert, D.C. & Ramadan, B.H. 2016 Chapter 4: the integral forms of the fundamental laws. In Mechanics of Fluids. Nelson Education.Google Scholar
Ray, S., Ünsal, B., Durst, F., Ertunc, Ö. & Bayoumi, O.A. 2005 Mass flow rate controlled fully developed laminar pulsating pipe flows. Trans. ASME J. Fluids Engng 127, 405–418.CrossRefGoogle Scholar
Rindt, C.C.M., Van Steenhoven, A.A., Janssen, J.D. & Vossers, G. 1991 Unsteady entrance flow in a $90^{\circ }$ curved tube. J. Fluid Mech. 226, 445–474.CrossRefGoogle Scholar
Siggers, J.H. & Waters, S.L. 2008 Unsteady flows in pipes with finite curvature. J. Fluid Mech. 600, 133–165.CrossRefGoogle Scholar
Singh, M.P. 1974 Entry flow in a curved pipe. J. Fluid Mech. 65, 517–539.CrossRefGoogle Scholar
Singh, P.J. & Madavan, N.K. 1987 Complete analysis and simulation of reciprocating pumps including system piping. In Proceedings 4th International Pump Users Symposium, pp. 55–74.Google Scholar
Smith, F.T. 1975 Pulsatile flow in curved pipes. J. Fluid Mech. 71, 15–42.CrossRefGoogle Scholar
Smith, F.T. 1976 Fluid flow into a curved pipe. Proc. R. Soc. Lond. A 351 (1664), 71–87.Google Scholar
Sudo, K., Sumida, M. & Yamane, R. 1992 Secondary motion of fully developed oscillatory flow in a curved pipe. J. Fluid Mech. 237, 189–208.CrossRefGoogle Scholar
Sumida, M. 2007 Pulsatile entrance flow in curved pipes: effect of various parameters. Exp. Fluids 43 (6), 949–958.CrossRefGoogle Scholar
Sumida, M., Sudou, K. & Wada, H. 1989 Pulsating flow in a curved pipe (secondary flow). Trans. JSME Intl J. Fluids Engng, Heat Transfer, Pow., Comb., Ther. Prop. 32 (4), 523–531.Google Scholar
Takeshi, N., Yoshihiro, N., Sachiko, K. & Kazuo, T. 1990 Developing oscillatory flow in a strongly curved tube. T. J. S. Mech. Engng B 56 (529), 2562–2569.Google Scholar
Tay, B.L. & Thorpe, R.B. 2014 Hydrodynamic forces acting on pipe bends in gas–liquid slug flow. Chem. Engng Res. Des. 92 (05), 812–825.CrossRefGoogle Scholar
Thomson, J. 1877 On the origin of windings of rivers in alluvial plains, with remarks on the flow of water round bends in pipes. Proc. R. Soc. Lond. A 25, 5–8.Google Scholar
Timite, B., Castelain, C. & Peerhossain, H. 2010 Pulsatile viscous flow in a curved pipe: effects of pulsation on the development of secondary flow. Intl J. Heat Fluid Flow 31 (05), 879–896.CrossRefGoogle Scholar
Tobak, M. & Peake, D.J. 1982 Topology of three-dimensional separated flows. Annu. Rev. Fluid Mech. 14 (1), 61–85.CrossRefGoogle Scholar
Uchida, S. 1956 The pulsating viscous flow superposed on the steady laminar motion of incompressible fluid in a circular pipe. Z. Angew. Math. Phys. 7 (5), 403–422.CrossRefGoogle Scholar
Venudas, P.A. & Manu, K.V. 2018 Analytical solution of transient pipe flow for an arbitrary inflow. In Proceedings 7th International 45th National Conference Fluid Mechanics Fluid Power, IIT Bombay.Google Scholar
Vester, A.K., Örlü, R. & Alfredsson, P.H. 2013 Vortical patterns in turbulent flow downstream a $90^{\circ }$ curved pipe at high Womersley numbers. Intl J. Heat Fluid Flow 44, 692–699.Google Scholar
Vester, A.K., Örlü, R. & Alfredsson, P.H. 2015 Pulsatile turbulent flow in straight and curved pipes – interpretation and decomposition of hot-wire signals. Flow Turbul. Combust. 94 (2), 305–321.CrossRefGoogle Scholar
Vester, A.K., Örlü, R. & Alfredsson, P.H. 2016 Turbulent flows in curved pipes: recent advances in experiments, simulations and analysis. Appl. Mech. Rev. 68 (5), 1–25.Google Scholar
Vetter, G. & Schweinfurther, F. 1987 Pressure pulsations in the piping of reciprocating pumps. Chem. Engng Technol. 10 (1), 262–271.CrossRefGoogle Scholar
Wachel, J.C., Tison, J.D. & Price, S.M. 1989 The effect of pulsations on cavitation in reciprocating pump systems. In Energy-Source Technol. Conference Exhibition, Houston, Texas, pp. 1–11.Google Scholar
White, F.M. 2016 Chapter 3: integral relations for a control volume. In Fluid Mechanics. McGraw-Hill Education.Google Scholar
Xiao, F., Jing, J., Han, L., Yang, L. & Wang, S. 2019 Modelling and analysis of impact forces acting on elbow in gas–liquid slug flow. Asia-Pacific J. Chem. Engng 14 (2), 1–17.Google Scholar
Yao, L.S. & Berger, S.A. 1975 Entry flow in a curved pipe. J. Fluid Mech. 67, 177–196.CrossRefGoogle Scholar
Yunus, A.C. 2017 Chapter 6: momentum analysis of flow systems. In Fluid Mechanics: Fundamentals and Applications. McGraw-Hill Education.Google Scholar
Supplementary material: File

Ahmed et al. supplementary material

Ahmed et al. supplementary material

Download Ahmed et al. supplementary material(File)
File 1.7 MB