Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T22:23:49.409Z Has data issue: false hasContentIssue false
  • English
  • Français

A homogenised model for flow, transport and sorption in a heterogeneous porous medium

Published online by Cambridge University Press:  09 December 2021

L.C. Auton Open the ORCID record for L.C. Auton [Opens in a new window] ,
S. Pramanik Open the ORCID record for S. Pramanik [Opens in a new window] ,
M.P. Dalwadi Open the ORCID record for M.P. Dalwadi [Opens in a new window] ,
C.W. MacMinn Open the ORCID record for C.W. MacMinn [Opens in a new window]  and
I.M. Griffiths Open the ORCID record for I.M. Griffiths [Opens in a new window]
L.C. Auton
Affiliation:
Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
S. Pramanik
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK Department of Mathematics, Indian Institute of Technology Gandhinagar, Palaj, Gandhinagar 382355, Gujarat, India
M.P. Dalwadi
Affiliation:
Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK Department of Mathematics, University College London, London WC1H 0AY, UK
C.W. MacMinn
Affiliation:
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, UK
I.M. Griffiths*
Affiliation:
Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK
*
†Email address for correspondence: Ian.Griffiths@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

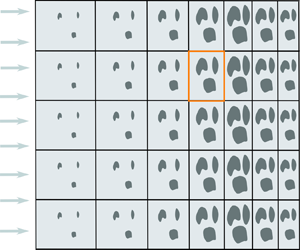
A major challenge in flow through porous media is to better understand the link between microstructure and macroscale flow and transport. For idealised microstructures, the mathematical framework of homogenisation theory can be used for this purpose. Here, we consider a two-dimensional microstructure comprising an array of obstacles of smooth but arbitrary shape, the size and spacing of which can vary along the length of the porous medium. We use homogenisation via the method of multiple scales to systematically upscale a novel problem involving cells of varying area to obtain effective continuum equations for macroscale flow and transport. The equations are characterised by the local porosity, a local anisotropic flow permeability, an effective local anisotropic solute diffusivity and an effective local adsorption rate. These macroscale properties depend non-trivially on the two degrees of microstructural geometric freedom in our problem: obstacle size and obstacle spacing. We exploit this dependence to construct and compare scenarios where the same porosity profile results from different combinations of obstacle size and spacing. We focus on a simple example geometry comprising circular obstacles on a rectangular lattice, for which we numerically determine the macroscale permeability and effective diffusivity. We investigate scenarios where the porosity is spatially uniform but the permeability and diffusivity are not. Our results may be useful in the design of filters or for studying the impact of deformation on transport in soft porous media.

JFM classification

Low-Reynolds-number flows: Porous media Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 932 , 10 February 2022 , A34
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

This author contributed significantly to this work.

References

REFERENCES

Auriault, J.-L. 1991 Heterogeneous medium. Is an equivalent macroscopic description possible? Intl J. Engng Sci. 29 (7), 785–795.CrossRefGoogle Scholar
Beckwith, C.W., Baird, A.J. & Heathwaite, A.L. 2003 Anisotropy and depth-related heterogeneity of hydraulic conductivity in a bog peat. II: modelling the effects on groundwater flow. Hydrol. Process. 17 (1), 103–113.CrossRefGoogle Scholar
Benítez, J.J., et al. 2012 Microfluidic extraction, stretching and analysis of human chromosomal DNA from single cells. Lab Chip 12, 4848–4854.CrossRefGoogle ScholarPubMed
Bensoussan, A., Lions, J.-L. & Papanicolaou, G. 2011 Asymptotic Analysis for Periodic Structures, vol. 374. American Mathematical Society.Google Scholar
Bruna, M. & Chapman, S.J. 2015 Diffusion in spatially varying porous media. SIAM J. Appl. Maths 75 (4), 1648–1674.CrossRefGoogle Scholar
Brusseau, M.L. 1994 Transport of reactive contaminants in heterogeneous porous media. Rev. Geophys. 32 (3), 285–313.CrossRefGoogle Scholar
Chapman, S.J. & McBurnie, S.E. 2011 A unified multiple-scales approach to one-dimensional composite materials and multiphase flow. SIAM J. Appl. Maths 71 (1), 200–217.CrossRefGoogle Scholar
Chapman, S.J., Shipley, R.J. & Jawad, R. 2008 Multiscale modeling of fluid transport in tumors. Bull. Math. Biol. 70, 2334–2357.CrossRefGoogle ScholarPubMed
Clavaud, J.-B., Maineult, A., Zamora, M., Rasolofosaon, P. & Schlitter, C. 2008 Permeability anisotropy and its relations with porous medium structure. J. Geophys. Res.: Solid Earth 113 (B1), B01202.Google Scholar
Dalwadi, M.P., Bruna, M. & Griffiths, I.M. 2016 A multiscale method to calculate filter blockage. J. Fluid Mech. 809, 264–289.CrossRefGoogle Scholar
Dalwadi, M.P., Griffiths, I.M. & Bruna, M. 2015 Understanding how porosity gradients can make a better filter using homogenization theory. Proc. R. Soc. Lond. A 471, 20150464.Google Scholar
Daly, K.R. & Roose, T. 2015 Homogenization of two fluid flow in porous media. Proc. R. Soc. Lond. A 471, 20140564.Google ScholarPubMed
Davit, Y., et al. 2013 a Homogenization via formal multiscale asymptotics and volume averaging: how do the two techniques compare? Adv. Water Resour. 62, 178–206.CrossRefGoogle Scholar
Davit, Y., Byrne, H., Osborne, J., Pitt-Francis, J., Gavaghan, D. & Quintard, M. 2013 b Hydrodynamic dispersion within porous biofilms. Phys. Rev. E 87 (1), 012718.CrossRefGoogle ScholarPubMed
Domenico, P.A. & Schwartz, F.W. 1990 Physical and Chemical Hydrogeology. Wiley.Google Scholar
Fritton, S.P. & Weinbaum, S. 2009 Fluid and solute transport in bone: flow-induced mechanotransduction. Annu. Rev. Fluid Mech. 41, 347–374.CrossRefGoogle ScholarPubMed
Hornung, U. 1996 Homogenization and Porous Media, vol. 6. Springer.Google Scholar
Kuwata, Y. & Suga, K. 2017 Direct numerical simulation of turbulence over anisotropic porous media. J. Fluid Mech. 831, 41–71.CrossRefGoogle Scholar
Li, N., et al. 2018 Suppressing dendritic lithium formation using porous media in lithium metal-based batteries. Nano Lett. 18, 2067–2073.CrossRefGoogle ScholarPubMed
Mariani, G., Fabbri, M., Negrini, F. & Ribani, P.L. 2010 High-gradient magnetic separation of pollutant from wastewaters using permanent magnets. Sep. Purif. Technol. 72, 147–155.CrossRefGoogle Scholar
Mauri, R. 1991 Dispersion, convection, and reaction in porous media. Phys. Fluids A: Fluid Dyn. 3 (5), 743–756.CrossRefGoogle Scholar
Mei, C.C. & Vernescu, B. 2010 Homogenization Methods for Multiscale Mechanics. World Scientific.CrossRefGoogle Scholar
Muntean, A. & Nikolopoulos, C. 2020 Colloidal transport in locally periodic evolving porous media – an upscaling exercise. SIAM J. Appl. Maths 80 (1), 448–475.CrossRefGoogle Scholar
van Noorden, T.L. 2009 Crystal precipitation and dissolution in a porous medium: effective equations and numerical experiments. Multiscale Model. Simul. 7 (3), 1220–1236.CrossRefGoogle Scholar
van Noorden, T.L. & Muntean, A. 2011 Homogenisation of a locally periodic medium with areas of low and high diffusivity. Eur. J. Appl. Maths 22 (5), 493–516.CrossRefGoogle Scholar
O'Dea, R.D., Nelson, M.R., El Haj, A.J., Waters, S.L. & Byrne, H.M. 2015 A multiscale analysis of nutrient transport and biological tissue growth in vitro. Math. Med. Biol. 32 (3), 345–366.CrossRefGoogle ScholarPubMed
Olivieri, S., Akoush, A., Brandt, L., Rosti, M.E. & Mazzino, A. 2020 Turbulence in a network of rigid fibers. Phys. Rev. Fluids 5, 074502.CrossRefGoogle Scholar
Printsypar, G., Bruna, M. & Griffiths, I.M. 2019 The influence of porous-medium microstructure on filtration. J. Fluid Mech. 861, 484–516.CrossRefGoogle Scholar
Quintard, M. & Whitaker, S. 1994 Convection, dispersion, and interfacial transport of contaminants: homogeneous porous media. Adv. Water Resour. 17, 221–239.CrossRefGoogle Scholar
Ray, N., van Noorden, T., Frank, F. & Knabner, P. 2012 Multiscale modeling of colloid and fluid dynamics in porous media including an evolving microstructure. Transp. Porous Med. 95, 669–696.CrossRefGoogle Scholar
Richardson, G. & Chapman, S.J. 2011 Derivation of the bidomain equations for a beating heart with a general microstructure. SIAM J. Appl. Maths 71 (3), 657–675.CrossRefGoogle Scholar
Rosti, M.E., Pramanik, S., Brandt, L. & Mitra, D. 2020 The breakdown of Darcy's law in a soft porous material. Soft Matt. 16, 939–944.CrossRefGoogle Scholar
Salles, J., Thovert, J.-F., Delannay, R., Prevors, L., Auriault, J.-L. & Adler, P.M. 1993 Taylor dispersion in porous media. Determination of the dispersion tensor. Phys. Fluids A: Fluid Dyn. 5 (10), 2348–2376.CrossRefGoogle Scholar
Shipley, R.J. & Chapman, S.J. 2010 Multiscale modelling of fluid and drug transport in vascular tumours. Bull. Math. Biol. 72, 1464–1491.CrossRefGoogle ScholarPubMed
Spychała, M. & Starzyk, J. 2015 Bacteria in non-woven textile filters for domestic wastewater treatment. Environ. Technol. 36 (8), 937–945.CrossRefGoogle ScholarPubMed
Tomin, P. & Lunati, I. 2016 Investigating Darcy-scale assumptions by means of a multiphysics algorithm. Adv. Water Resour. 95, 80–91.CrossRefGoogle Scholar
Valdés-Parada, F.J. & Alvarez-Ramírez, J. 2011 A volume averaging approach for asymmetric diffusion in porous media. J. Chem. Phys. 134 (20), 204709.CrossRefGoogle ScholarPubMed
Wang, M., Liu, H., Zak, D. & Lennartz, B. 2020 Effect of anisotropy on solute transport in degraded fen peat soils. Hydrol. Process. 34 (9), 2128–2138.CrossRefGoogle Scholar
Wang, Z., Wu, H.-J., Fine, D., Schmulen, J., Hu, Y., Godin, B., Zhang, J.X.J. & Liu, X. 2013 Ciliated micropillars for the microfluidic-based isolation of nanoscale lipid vesicles. Lab Chip 13, 2879–2882.CrossRefGoogle ScholarPubMed
Whitaker, S. 1986 Flow in porous media I: a theoretical derivation of Darcy's law. Transp. Porous Med. 1, 3–25.CrossRefGoogle Scholar
Whitaker, S. 2013 The Method of Volume Averaging. Springer.Google Scholar
Wood, B.D., Cherblanc, F., Quintard, M. & Whitaker, S. 2003 Volume averaging for determining the effective dispersion tensor: closure using periodic unit cells and comparison with ensemble averaging. Water Resour. Res. 39 (8), 1210.CrossRefGoogle Scholar