Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T13:05:40.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Horizontal convective flow from a line heat source located at the liquid–gas interface in presence of surface film

Published online by Cambridge University Press:  30 June 2022

Yu.K. Rudenko Open the ORCID record for Yu.K. Rudenko [Opens in a new window] ,
N.A. Vinnichenko Open the ORCID record for N.A. Vinnichenko [Opens in a new window] ,
Yu.Yu. Plaksina ,
A.V. Pushtaev Open the ORCID record for A.V. Pushtaev [Opens in a new window]  and
A.V. Uvarov
Yu.K. Rudenko*
Affiliation:
Faculty of Physics, Lomonosov Moscow State University, Leninskiye Gory, 1/2, Moscow 119991, Russia
N.A. Vinnichenko
Affiliation:
Faculty of Physics, Lomonosov Moscow State University, Leninskiye Gory, 1/2, Moscow 119991, Russia
Yu.Yu. Plaksina
Affiliation:
Faculty of Physics, Lomonosov Moscow State University, Leninskiye Gory, 1/2, Moscow 119991, Russia
A.V. Pushtaev
Affiliation:
Faculty of Physics, Lomonosov Moscow State University, Leninskiye Gory, 1/2, Moscow 119991, Russia
A.V. Uvarov
Affiliation:
Faculty of Physics, Lomonosov Moscow State University, Leninskiye Gory, 1/2, Moscow 119991, Russia
*
†Email address for correspondence: ykrudenko@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

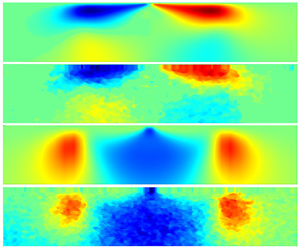
Development of the convective flow from a line heat source located at the liquid surface is studied for the case when thermocapillary convection is inhibited by the surface film. Surface film is formed by small amounts of surfactants present in non-deionized (distilled or natural) water. It imposes a no-slip boundary condition for velocity at the surface and determines the fluid dynamics of the surface layer. For the heat source located at the surface, the vertical stratification is stable and the flow is driven by a horizontal pressure gradient, formed by non-uniform heating of the liquid along the surface. Experimental studies include measurements of velocity fields using particle image velocimetry, surface relief measurements using moon-glade background oriented Schlieren and surface temperature measurements using infrared thermography. Also, numerical simulations of the flow development are performed and a new similarity solution for the steady state in a laterally unbounded domain is constructed, which takes into account the pressure gradient. The results are shown to be in good agreement with experimental data. The obtained dependencies of the maximal velocity, boundary layer thickness, local and total Nusselt numbers on the Rayleigh number are consistent with literature data obtained for the non-uniformly heated bottom case, which demonstrates universal properties of horizontal convection.

JFM classification

Boundary Layers: Boundary layer structure Convection: Buoyant boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 944 , 10 August 2022 , A35
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Berg, J.C., Boudart, M. & Acrivos, A. 1966 Natural convection in pools of evaporating liquids. J. Fluid Mech. 24, 721–735.CrossRefGoogle Scholar
Boetcher, S.K.S. 2014 Natural Convection from Circular Cylinders. Springer.CrossRefGoogle Scholar
Chiu-Webster, S., Hinch, E.J. & Lister, J.R. 2008 Very viscous horizontal convection. J. Fluid Mech. 611, 395–426.CrossRefGoogle Scholar
Daniels, P.G. 2010 On the boundary-layer structure of high-Prandtl-number horizontal convection. J. Fluid Mech. 652, 299–331.CrossRefGoogle Scholar
Earnshaw, J.C. 1997 Surface light scattering: a methodological review. Appl. Opt. 36, 7583–7592.CrossRefGoogle ScholarPubMed
Fujii, T. 1963 Theory of the steady laminar natural convectiol above a horizontal line heat source and a point heat source. Intl J. Heat Mass Transfer 6, 597–606.CrossRefGoogle Scholar
Gayen, B., Griffiths, R.W. & Hughes, G.O. 2014 Stability transitions and turbulence in horizontal convection. J. Fluid Mech. 751, 698–724.CrossRefGoogle Scholar
Gebhart, B., Pera, L. & Schorr, A.W. 1970 Steady laminar natural convection plumes above a horizontal line heat source. Intl J. Heat Mass Transfer 13, 161–171.CrossRefGoogle Scholar
Glauert, M.B. 1956 The wall jet. J. Fluid Mech. 1, 625–643.CrossRefGoogle Scholar
Hughes, G.O. & Griffiths, R.W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.CrossRefGoogle Scholar
Kuehner, J.P., Hamed, A.M. & Mitchell, J.D. 2015 Experimental investigation of the free convection velocity boundary layer and plume formation region for a heated horizontal cylinder. Intl J. Heat Mass Transfer 82, 78–97.CrossRefGoogle Scholar
Kurosaki, Y., Satoh, I., Horiuchi, T. & Kashiwagi, T. 1989 Effect of Marangoni convection on the temperature profiles of a free surface subject to nonuniform radiative heating. Exp. Therm. Fluid Sci. 2, 365–373.CrossRefGoogle Scholar
Liñán, A. & Kurdyumov, V.N. 1998 Laminar free convection induced by a line heat source, and heat transfer from wires at small Grashof numbers. J. Fluid Mech. 362, 199–227.CrossRefGoogle Scholar
Lohse, D. & Zhang, X. 2020 Physicochemical hydrodynamics of droplets out of equilibrium. Nat. Rev. Phys. 2, 426–443.CrossRefGoogle Scholar
Mori, A. & Niino, H. 2002 Time evolution of nonlinear horizontal convection: its flow regimes and self-similar solutions. J. Atmos. Sci. 59 (11), 1841–1856.2.0.CO;2>CrossRefGoogle Scholar
Mullarney, J.C., Griffiths, R.W. & Hughes, G.O. 2004 Convection driven by differential heating at a horizontal boundary. J. Fluid Mech. 516, 181–209.CrossRefGoogle Scholar
Nepomnyashchy, A.A., Velarde, M.G. & Colinet, P. 2001 Interfacial Phenomena and Convection. Chapman & Hall.CrossRefGoogle Scholar
Noto, D., Terada, T., Yanagisawa, T., Miyagoshi, T. & Tasaka, Y. 2021 Developing horizontal convection against stable temperature stratification in a rectangular container. Phys. Rev. Fluids 6, 083501.CrossRefGoogle Scholar
Paparella, F. & Young, W.R. 2002 Horizontal convection is non-turbulent. J. Fluid Mech. 466, 205–214.CrossRefGoogle Scholar
Pawliszak, P., Ulaganathan, V., Bradshaw-Hajek, B.H., Manica, R., Beattie, D.A. & Krasowska, M. 2019 Mobile or immobile? Rise velocity of air bubbles in high-purity water. J. Phys. Chem. C 123, 15131–15138.CrossRefGoogle Scholar
Phares, D.J., Smedley, G.T. & Flagan, R.C. 2000 The inviscid impingement of a jet with arbitrary velocity profile. Phys. Fluids 12, 2046–2055.CrossRefGoogle Scholar
Pigeonneau, F. & Flesselles, J.M. 2012 Practical laws for natural convection of viscous fluids heated from above in a shallow cavity. Intl J. Heat Mass Transfer 55, 436–442.CrossRefGoogle Scholar
Plaksina, Yu.Yu., Pushtaev, A.V., Vinnichenko, N.A. & Uvarov, A.V. 2018 The effects of small contaminants on the formation of structures during Rayleigh–Bénard–Marangoni convection in a planar liquid layer. Mosc. Univ. Phys. Bull. 73, 513–519.CrossRefGoogle Scholar
Plaksina, Yu.Yu., Uvarov, A.V., Vinnichenko, N.A. & Lapshin, V.B. 2012 Experimental investigation of near-surface small-scale structures at water-air interface: background oriented Schlieren and thermal imaging of water surface. Russ. J. Earth Sci. 12, ES4002.CrossRefGoogle Scholar
Ramme, L. & Hansen, U. 2019 Transition to time-dependent flow in highly viscous horizontal convection. Phys. Rev. Fluids 4, 093501.CrossRefGoogle Scholar
Reiter, P. & Shishkina, O. 2020 Classical and symmetrical horizontal convection: detaching plumes and oscillations. J. Fluid Mech. 892, R1.CrossRefGoogle Scholar
Rocha, C.B., Bossy, T., Llewellyn Smith, S.G. & Young, W.R. 2020 a Improved bounds on horizontal convection. J. Fluid Mech. 883, A41.CrossRefGoogle Scholar
Rocha, C.B., Constantinou, N.C., Llewellyn Smith, S.G. & Young, W.R. 2020 b The Nusselt numbers of horizontal convection. J. Fluid Mech. 894, A24.CrossRefGoogle Scholar
Rossby, H.T. 1965 On thermal convection driven by non-uniform heating from below: an experimental study. Deep-Sea Res. 12, 9–16.Google Scholar
Sanmiguel Vila, C., Discetti, S., Carlomagno, G.M., Astarita, T. & Ianiro, A. 2016 On the onset of horizontal convection. Intl J. Therm. Sci. 110, 96–108.CrossRefGoogle Scholar
Saylor, J.R., Smith, G.B. & Flack, K.A. 2001 An experimental investigation of the surface temperature field during evaporative convection. Phys. Fluids 13, 428–439.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2017 Boundary-Layer Theory, 9th edn. Springer.CrossRefGoogle Scholar
Scotti, A. & White, B. 2011 Is horizontal convection really non-turbulent? Geophys. Res. Lett. 38, L21609.CrossRefGoogle Scholar
Shishkina, O. 2017 Mean flow structure in horizontal convection. J. Fluid Mech. 812, 525–540.CrossRefGoogle Scholar
Siggers, J.H., Kerswell, R.R. & Balmforth, N.J. 2004 Bounds on horizontal convection. J. Fluid. Mech. 517, 55–70.CrossRefGoogle Scholar
Stommel, H. 1962 On the smallness of sinking regions in the ocean. Proc. Natl Acad. Sci. USA 48, 766–772.CrossRefGoogle ScholarPubMed
Vinnichenko, N.A., Plaksina, Yu.Yu., Baranova, K.M., Pushtaev, A.V. & Uvarov, A.V. 2018 a Mobility of free surface in different liquids and its influence on water striders locomotion. Environ. Fluid Mech. 18, 1045–1056.CrossRefGoogle Scholar
Vinnichenko, N.A., Pushtaev, A.V., Plaksina, Yu.Yu., Rudenko, Yu.K. & Uvarov, A.V. 2018 b Horizontal convection driven by nonuniform radiative heating in liquids with different surface behavior. Intl J. Heat Mass Transfer 126, 400–410.CrossRefGoogle Scholar
Vinnichenko, N.A., Pushtaev, A.V., Plaksina, Yu.Yu. & Uvarov, A.V. 2020 Measurements of liquid surface relief with moon-glade background oriented Schlieren technique. Exp. Therm. Fluid Sci. 114, 110051.CrossRefGoogle Scholar
Vinnichenko, N.A., Uvarov, A.V. & Plaksina, Yu.Yu. 2014 Combined study of heat exchange near the liquid–gas interface by means of background oriented Schlieren and infrared thermal imaging. Exp. Therm. Fluid Sci. 59, 238–245.CrossRefGoogle Scholar
Ẇhlin, A.K., Johansson, A.M., Aas, E., Broström, G., Weber, J.E.H. & Grue, J. 2016 Horizontal convection in water heated by infrared radiation and cooled by evaporation: scaling analysis and experimental results. Tellus A 62A, 154–169.Google Scholar
Wang, W. & Huang, R.X. 2005 An experimental study on thermal circulation driven by horizontal differential heating. J. Fluid. Mech. 540, 49–73.CrossRefGoogle Scholar
Yan, B., Shishkina, O. & He, X. 2021 Thermal boundary-layer structure in laminar horizontal convection. J. Fluid Mech. 915, R5.CrossRefGoogle Scholar
Supplementary material: File

Rudenko et al. supplementary material

Rudenko et al. supplementary material

Download Rudenko et al. supplementary material(File)
File 3.7 MB