Article contents
Horizontal locomotion of a vertically flapping oblate spheroid
Published online by Cambridge University Press: 15 February 2018
Abstract
We consider the self-induced motions of three-dimensional oblate spheroids of density 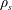 $\unicode[STIX]{x1D70C}_{s}$ with varying aspect ratios
$\unicode[STIX]{x1D70C}_{s}$ with varying aspect ratios 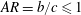 $AR=b/c\leqslant 1$ , where
$AR=b/c\leqslant 1$ , where 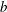 $b$ and
$b$ and  $c$ are the spheroids’ centre-pole radius and centre-equator radius, respectively. Vertical motion is imposed on the spheroids such that
$c$ are the spheroids’ centre-pole radius and centre-equator radius, respectively. Vertical motion is imposed on the spheroids such that 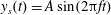 $y_{s}(t)=A\sin (2\unicode[STIX]{x03C0}ft)$ in a fluid of density
$y_{s}(t)=A\sin (2\unicode[STIX]{x03C0}ft)$ in a fluid of density 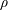 $\unicode[STIX]{x1D70C}$ and kinematic viscosity
$\unicode[STIX]{x1D70C}$ and kinematic viscosity  $\unicode[STIX]{x1D708}$ . As in strictly two-dimensional flows, above a critical value
$\unicode[STIX]{x1D708}$ . As in strictly two-dimensional flows, above a critical value 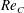 $Re_{C}$ of the flapping Reynolds number
$Re_{C}$ of the flapping Reynolds number 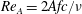 $Re_{A}=2Afc/\unicode[STIX]{x1D708}$ , the spheroid ultimately propels itself horizontally as a result of fluid–body interactions. For
$Re_{A}=2Afc/\unicode[STIX]{x1D708}$ , the spheroid ultimately propels itself horizontally as a result of fluid–body interactions. For 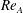 $Re_{A}$ sufficiently above
$Re_{A}$ sufficiently above 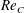 $Re_{C}$ , the spheroid rapidly settles into a terminal state of constant, unidirectional velocity, consistent with the prediction of Deng et al. (Phys. Rev. E, vol. 94, 2016, 033107) that, at sufficiently high
$Re_{C}$ , the spheroid rapidly settles into a terminal state of constant, unidirectional velocity, consistent with the prediction of Deng et al. (Phys. Rev. E, vol. 94, 2016, 033107) that, at sufficiently high 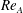 $Re_{A}$ , such oscillating spheroids manifest
$Re_{A}$ , such oscillating spheroids manifest 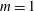 $m=1$ asymmetric flow, with characteristic vortical structures conducive to providing unidirectional thrust if the spheroid is free to move horizontally. The speed
$m=1$ asymmetric flow, with characteristic vortical structures conducive to providing unidirectional thrust if the spheroid is free to move horizontally. The speed 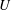 $U$ of propagation increases linearly with the flapping frequency, resulting in a constant Strouhal number
$U$ of propagation increases linearly with the flapping frequency, resulting in a constant Strouhal number 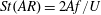 $St(AR)=2Af/U$ , characterising the locomotive performance of the oblate spheroid, somewhat larger than the equivalent
$St(AR)=2Af/U$ , characterising the locomotive performance of the oblate spheroid, somewhat larger than the equivalent  $St$ for two-dimensional spheroids, demonstrating that the three-dimensional flow is less efficient at driving locomotion.
$St$ for two-dimensional spheroids, demonstrating that the three-dimensional flow is less efficient at driving locomotion.  $St$ decreases with increasing aspect ratio for both two-dimensional and three-dimensional flows, although the relative disparity (and hence relative inefficiency of three-dimensional motion) decreases. For flows with
$St$ decreases with increasing aspect ratio for both two-dimensional and three-dimensional flows, although the relative disparity (and hence relative inefficiency of three-dimensional motion) decreases. For flows with 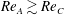 $Re_{A}\gtrsim Re_{C}$ , we observe two distinct types of inherently three-dimensional motion for different aspect ratios. The first, associated with a disk of aspect ratio
$Re_{A}\gtrsim Re_{C}$ , we observe two distinct types of inherently three-dimensional motion for different aspect ratios. The first, associated with a disk of aspect ratio 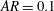 $AR=0.1$ at
$AR=0.1$ at 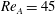 $Re_{A}=45$ , consists of a ‘stair-step’ trajectory. This trajectory can be understood through consideration of relatively high azimuthal wavenumber instabilities of interacting vortex rings, characterised by in-phase vortical structures above and below an oscillating spheroid, recently calculated using Floquet analysis by Deng et al. (Phys. Rev. E, vol. 94, 2016, 033107). Such ‘in-phase’ instabilities arise in a relatively narrow band of
$Re_{A}=45$ , consists of a ‘stair-step’ trajectory. This trajectory can be understood through consideration of relatively high azimuthal wavenumber instabilities of interacting vortex rings, characterised by in-phase vortical structures above and below an oscillating spheroid, recently calculated using Floquet analysis by Deng et al. (Phys. Rev. E, vol. 94, 2016, 033107). Such ‘in-phase’ instabilities arise in a relatively narrow band of 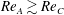 $Re_{A}\gtrsim Re_{C}$ , which band shifts to higher Reynolds number as the aspect ratio increases. (Indeed, for horizontally fixed spheroids with aspect ratio
$Re_{A}\gtrsim Re_{C}$ , which band shifts to higher Reynolds number as the aspect ratio increases. (Indeed, for horizontally fixed spheroids with aspect ratio  $AR=0.2$ , Floquet analysis actually predicts stability at
$AR=0.2$ , Floquet analysis actually predicts stability at 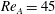 $Re_{A}=45$ .) For such a spheroid (
$Re_{A}=45$ .) For such a spheroid ( 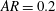 $AR=0.2$ ,
$AR=0.2$ , 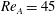 $Re_{A}=45$ , with sufficiently small mass ratio
$Re_{A}=45$ , with sufficiently small mass ratio 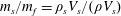 $m_{s}/m_{f}=\unicode[STIX]{x1D70C}_{s}V_{s}/(\unicode[STIX]{x1D70C}V_{s})$ , where
$m_{s}/m_{f}=\unicode[STIX]{x1D70C}_{s}V_{s}/(\unicode[STIX]{x1D70C}V_{s})$ , where  $V_{s}$ is the volume of the spheroid) which is free to move horizontally, the second type of three-dimensional motion is observed, initially taking the form of a ‘snaking’ trajectory with long quasi-periodic sweeping oscillations before locking into an approximately elliptical ‘orbit’, apparently manifesting a three-dimensional generalisation of the
$V_{s}$ is the volume of the spheroid) which is free to move horizontally, the second type of three-dimensional motion is observed, initially taking the form of a ‘snaking’ trajectory with long quasi-periodic sweeping oscillations before locking into an approximately elliptical ‘orbit’, apparently manifesting a three-dimensional generalisation of the 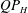 $QP_{H}$ quasi-periodic symmetry breaking discussed for sufficiently high aspect ratio two-dimensional elliptical foils in Deng & Caulfield (J. Fluid Mech., vol. 787, 2016, pp. 16–49).
$QP_{H}$ quasi-periodic symmetry breaking discussed for sufficiently high aspect ratio two-dimensional elliptical foils in Deng & Caulfield (J. Fluid Mech., vol. 787, 2016, pp. 16–49).
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 10
- Cited by

