Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T09:18:01.133Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydraulic jump on the surface of a cone

Published online by Cambridge University Press:  04 November 2022

Guangzhao Zhou Open the ORCID record for Guangzhao Zhou [Opens in a new window]  and
Andrea Prosperetti Open the ORCID record for Andrea Prosperetti [Opens in a new window]
Guangzhao Zhou
Affiliation:
Department of Mechanical Engineering, University of Houston, Houston, TX 77204, USA
Andrea Prosperetti*
Affiliation:
Department of Mechanical Engineering, University of Houston, Houston, TX 77204, USA Faculty of Science and Technology, and J. M. Burgers Center for Fluid Dynamics, University of Twente, 7500 AE Enschede, The Netherlands Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: aprosper@central.uh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

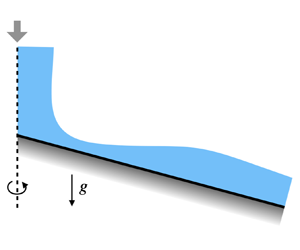
This paper addresses several aspects of the axisymmetric flow of a liquid film over the surface of a downward-sloping cone. The study is rooted on a validated computational tool the results of which are interpreted with the help of a hyperbolic time-dependent reduced-order model also derived in the paper. The steady version of the model demonstrates the weakening and ultimate disappearance of the circular hydraulic jump as the cone surface transitions from planar to downward sloping. Mathematically, this evolution is reflected in a change of the model's critical point from spiral to node. A significant advantage of the time-dependent model is that, when it is integrated in time, the flow regions upstream and downstream of the critical point are connected. Due to this feature, when a hydraulic jump exists, its position can be sharply captured automatically with a good agreement with Navier–Stokes simulations. Surface-tension effects are properly accounted for and, in steady conditions, are shown to have a marginal effect on the flow, including the position of the hydraulic jump. A correlation is obtained for the jump radius as a function of the flow rate, liquid viscosity, gravitational acceleration and the angle of inclination of the cone surface. In a suitable limit, the model reduces to the optimal two-dimensional, first-order model for liquid film flow down an inclined plane and, in a different limit, it describes an axisymmetric thin liquid film falling down the surface of a vertical cylinder. Some results are also presented for the waves induced by a pulsating jet on the surface of the liquid film and for a jet impinging on the surface of a cone from below.

JFM classification

Interfacial Flows (free surface): Thin films Materials Processing Flows: Coating
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 951 , 25 November 2022 , A20
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: School of Engineering Science, University of Chinese Academy of Sciences, Beijing 101408, PR China.

References

Adachi, T., Takahashi, Y. & Okajima, J. 2018 Film flow thickness along the outer surface of rotating cones. Eur. J. Mech. (B/Fluids) 68, 39–44.CrossRefGoogle Scholar
Al-Hawaj, O. 1999 A numerical study of the hydrodynamics of a falling liquid film on the internal surface of a downward tapered cone. Chem. Engng J. 75, 177–182.CrossRefGoogle Scholar
Albert, C., Marschall, H. & Bothe, D. 2014 Direct numerical simulation of interfacial mass transfer into falling films. Intl J. Heat Mass Transfer 69, 343–357.CrossRefGoogle Scholar
Askarizadeh, H., Ahmadikia, H., Ehrenpreis, C., Kneer, R., Pishevar, A. & Rohlfs, W. 2019 Role of gravity and capillary waves in the origin of circular hydraulic jumps. Phys. Rev. Fluids 4, 114002.CrossRefGoogle Scholar
Askarizadeh, H., Ahmadikia, H., Ehrenpreis, C., Kneer, R., Pishevar, A. & Rohlfs, W. 2020 Heat transfer in the hydraulic jump region of circular free-surface liquid jets. Intl J. Heat Mass Transfer 146, 118823.CrossRefGoogle Scholar
Balestra, G., Nguyen, D.M.-P. & Gallaire, F. 2018 Rayleigh–Taylor instability under a spherical substrate. Phys. Rev. Fluids 3, 084005.CrossRefGoogle Scholar
Benilov, E.S.. 2014 Depth-averaged model for hydraulic jumps on an inclined plate. Phys. Rev. E89, 053013.Google Scholar
Bhagat, R.K., Jha, N.K., Linden, P.F. & Wilson, D.I. 2018 On the origin of the circular hydraulic jump in a thin liquid film. J. Fluid Mech. 851, R5.CrossRefGoogle Scholar
Bhagat, R.K. & Linden, P.F. 2020 The circular capillary jump. J. Fluid Mech. 896, A25.CrossRefGoogle Scholar
Bhagat, R.K., Wilson, I.D. & Linden, P.F. 2020 Experimental evidence for surface tension origin of the circular hydraulic jump. arXiv:2010.04107v3.Google Scholar
Bogacki, P. & Shampine, L.F. 1989 A 3(2) pair of Runge–Kutta formulas. Appl. Maths Lett. 2, 321–325.CrossRefGoogle Scholar
Bohr, T., Dimon, P. & Putkaradze, V. 1993 Shallow-water approach to the circular hydraulic jump. J. Fluid Mech. 254, 635–648.CrossRefGoogle Scholar
Bohr, T., Ellegaard, C., Espe Hansen, A., Hansen, K., Haaning, A., Putkaradze, V. & Watanabe, S. 1998 Separation and pattern formation in hydraulic jumps. Physica A 249, 111–117.CrossRefGoogle Scholar
Bohr, T., Ellegaard, C., Hansen, A.E. & Haaning, A. 1996 Hydraulic jumps, flow separation and wave breaking: an experimental study. Physica B 228, 1–10.CrossRefGoogle Scholar
Bohr, T., Putkaradze, V. & Watanabe, S. 1997 Averaging theory for the structure of hydraulic jumps and separation in laminar free-surface flows. Phys. Rev. Lett. 79, 1038–1041.CrossRefGoogle Scholar
Brackbill, J.U., Kothe, D.B. & Zemach, C. 1992 A continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354.CrossRefGoogle Scholar
Brechet, Y. & Néda, Z. 1999 On the circular hydraulic jump. Am. J. Phys. 67, 723–731.CrossRefGoogle Scholar
Brun, P.-T., Damiano, A., Rieu, P., Balestra, G. & Gallaire, F. 2015 Rayleigh–Taylor instability under an inclined plane. Phys. Fluids 27, 084107.CrossRefGoogle Scholar
Bush, J.W.M. & Aristoff, J.M. 2003 The influence of surface tension on the circular hydraulic jump. J. Fluid Mech. 489, 229–238.CrossRefGoogle Scholar
Button, E.C., Davidson, J.F., Jameson, G.J. & Sader, J.E. 2010 Water bells formed on the underside of a horizontal plate. Part 2. Theory. J. Fluid Mech. 649, 45–68.CrossRefGoogle Scholar
Chakraborty, S., Nguyen, P.-K., Ruyer-Quil, C. & Bontozoglou, V. 2014 Extreme solitary waves on falling liquid films. J. Fluid Mech. 745, 564–591.CrossRefGoogle Scholar
Chang, H.-C. & Demekhin, E.A. 2002 Complex Wave Dynamics on Thin Films. Elsevier.Google Scholar
Charogiannis, A. & Markides, C.N. 2019 Spatiotemporally resolved heat transfer measurements in falling liquid-films by simultaneous application of planar laser-induced fluorescence (PLIF), particle tracking velocimetry (PTV) and infrared (IR) thermography. Exp. Therm. Fluid Sci. 107, 169–191.CrossRefGoogle Scholar
Clanet, C. 2007 Waterbells and liquid sheets. Annu. Rev. Fluid Mech. 39, 469–496.CrossRefGoogle Scholar
Dasgupta, R. & Govindarajan, R. 2010 Nonsimilar solutions of the viscous shallow water equations governing weak hydraulic jumps. Phys. Fluids 22, 112108.CrossRefGoogle Scholar
Dasgupta, R., Tomar, G. & Govindarajan, R. 2015 Numerical study of laminar, standing hydraulic jumps in a planar geometry. Eur. Phys. J. E 38, 45.CrossRefGoogle Scholar
De Vita, F., Lagrée, P.-Y., Chibbaro, S. & Popinet, S. 2020 Beyond shallow water: appraisal of a numerical approach to hydraulic jumps based upon the boundary layer theory. Eur. J. Mech. (B/Fluids) 79, 233–246.CrossRefGoogle Scholar
Dhar, M., Das, G. & Das, P.K. 2020 Planar hydraulic jumps in thin film flow. J. Fluid Mech. 884, A11.CrossRefGoogle Scholar
Ding, Z. & Wong, T.N. 2017 Three-dimensional dynamics of thin liquid films on vertical cylinders with Marangoni effect. Phys. Fluids 29, 011701.CrossRefGoogle Scholar
Duchesne, A., Andersen, A. & Bohr, T. 2019 Surface tension and the origin of the circular hydraulic jump in a thin liquid film. Phys. Rev. Fluids 4, 084001.CrossRefGoogle Scholar
Duchesne, A., Lebon, L. & Limat, L. 2014 Constant Froude number in a circular hydraulic jump and its implication on the jump radius selection. Europhys. Lett. 107, 54002.CrossRefGoogle Scholar
Duchesne, A. & Limat, L. 2022 Circular hydraulic jumps: where does surface tension matter? J. Fluid Mech. 937, R2.CrossRefGoogle Scholar
Fernandez-Feria, R., Sanmiguel-Rojas, E. & Benilov, E.S. 2019 On the origin and structure of a stationary circular hydraulic jump. Phys. Fluids 31, 072104.CrossRefGoogle Scholar
Frenkel, A.L. 1992 Nonlinear theory of strongly undulating thin films flowing down vertical cylinders. Europhys. Lett. 18, 583–588.CrossRefGoogle Scholar
Glendinning, P. 1994 Stability, Instability and Chaos. Cambridge University Press.CrossRefGoogle Scholar
Hansen, S.H., Hørlück, S., Zauner, D., Dimon, P., Ellegaard, C. & Creagh, S.C. 1997 Geometric orbits of surface waves from a circular hydraulic jump. Phys. Rev. E 55, 7048–7061.CrossRefGoogle Scholar
Higuera, F.J. 1994 The hydraulic jump in a viscous laminar flow. J. Fluid Mech. 274, 69–92.CrossRefGoogle Scholar
Indeikina, A., Veretennikov, I. & Chang, H.-C. 1997 Drop fall-off from pendent rivulets. J. Fluid Mech. 338, 173–201.CrossRefGoogle Scholar
Issa, R.I. 1986 Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.CrossRefGoogle Scholar
Jambon-Puillet, E., Ledda, P.G., Gallaire, F. & Brun, P.-T. 2021 Drops on the underside of a slightly inclined wet substrate move too fast to grow. Phys. Rev. Lett. 127, 044503.CrossRefGoogle Scholar
Jameson, A., Schmidt, W. & Turkel, E. 1981 Numerical solution of the Euler equations by finite volume methods using Runge Kutta time stepping schemes. AIAA 14th Fluid and Plasma Dynamics Conference, Palo Alto CA. AIAA Paper 81-1259.Google Scholar
Jameson, G.J., Jenkins, C.E., Button, E.C. & Sader, J.E. 2010 Water bells formed on the underside of a horizontal plate. Part 1. Experimental investigation. J. Fluid Mech. 649, 19–43.CrossRefGoogle Scholar
Ji, H., Falcon, C., Sadeghpour, A., Zeng, Z., Ju, Y.S. & Bertozzi, A.L. 2019 Dynamics of thin liquid films on vertical cylindrical fibres. J. Fluid Mech. 865, 303–327.CrossRefGoogle Scholar
Kalliadasis, S. & Chang, H.-C. 1994 Drop formation during coating of vertical fibres. J. Fluid Mech. 261, 135–168.CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M.G. 2012 Falling Liquid Films. Springer.CrossRefGoogle Scholar
Kasimov, A.R. 2008 A stationary circular hydraulic jump, the limits of its existence and its gasdynamic analogue. J. Fluid Mech. 601, 189–198.CrossRefGoogle Scholar
Kofman, N., Rohlfs, W., Gallaire, F., Scheid, B. & Ruyer-Quil, C. 2018 Prediction of two-dimensional dripping onset of a liquid film under an inclined plane. Intl J. Multiphase Flow 104, 286–293.CrossRefGoogle Scholar
Kurihara, M. 1946 Laminar flow in a horizontal liquid layer. Report of the Research Institute for Fluid Engineering, Kyusyu Imperial University, vol. 3, pp. 11–33.Google Scholar
Lagerstrom, P.A. & Casten, R.G. 1972 Basic concepts underlying singular perturbation techniques. SIAM Rev. 14, 63–120.CrossRefGoogle Scholar
Leal, L.G. 2007 Advanced Transport Phenomena. Cambridge University Press.CrossRefGoogle Scholar
Ledda, P.G., Balestra, G., Lerisson, G., Scheid, B., Wyart, M. & Gallaire, F. 2021 Hydrodynamic-driven morphogenesis of karst draperies: spatio-temporal analysis of the two-dimensional impulse response. J. Fluid Mech. 910, A53.CrossRefGoogle Scholar
Lee, A., Brun, P.-T., Marthelot, J., Balestra, G., Gallaire, F. & Reis, P.M. 2016 Fabrication of slender elastic shells by the coating of curved surfaces. Nat. Commun. 7, 11155.CrossRefGoogle ScholarPubMed
Lefschetz, S. 1963 Differential Equations: Geometric Theory, 2nd edn. Interscience Publishers, reprinted by Dover, New York, 1977.Google Scholar
Lerisson, G., Ledda, P.G., Balestra, G. & Gallaire, F. 2020 Instability of a thin viscous film flowing under an inclined substrate: steady patterns. J. Fluid Mech. 898, A6.CrossRefGoogle Scholar
Lin, T.-S., Dijksman, J.A. & Kondic, L. 2021 Thin liquid films in a funnel. J. Fluid Mech. 924, A26.CrossRefGoogle Scholar
Mathur, M., Dasgupta, R., Selvi, N.R., John, N.S., Kulkarni, G.U. & Govindarajan, R. 2007 Gravity-free hydraulic jumps and metal femtoliter cups. Phys. Rev. Lett. 98, 164502.CrossRefGoogle ScholarPubMed
Mohajer, B. & Li, R. 2015 Circular hydraulic jump on finite surfaces with capillary limit. Phys. Fluids 27, 117102.CrossRefGoogle Scholar
Oron, A., Davis, S.H. & Bankoff, S.G. 1997 Long-scale evolution of thin liquid films. Revs. Mod. Phys. 69, 931–980.CrossRefGoogle Scholar
Park, C.D., Nosoko, T., Gima, S. & Ro, S.T. 2004 Wave-augmented mass transfer in a liquid film falling inside a vertical tube. Intl J. Heat Mass Transfer 47, 2587–2598.CrossRefGoogle Scholar
Roenby, J., Bredmose, H. & Jasak, H. 2016 A computational method for sharp interface advection. Roy. Soc. Open Sci. 3, 160405.CrossRefGoogle ScholarPubMed
Rojas, N., Argentina, M. & Tirapegui, E. 2013 A progressive correction to the circular hydraulic jump scaling. Phys. Fluids 25, 042105.CrossRefGoogle Scholar
Rojas, N.O., Argentina, M., Cerda, E. & Tirapegui, E. 2010 Inertial lubrication theory. Phys. Rev. Lett. 104, 187801.CrossRefGoogle ScholarPubMed
Ruyer-Quil, C. & Manneville, P. 1998 Modeling film flows down inclined planes. Eur. Phys. J. B 6, 227–292.CrossRefGoogle Scholar
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15, 357–369.CrossRefGoogle Scholar
Ruyer-Quil, C., Treveleyan, P., Giorgiutti-Dauphiné, F., Duprat, C. & Kalliadasis, S. 2008 Modelling film flows down a fibre. J. Fluid Mech. 603, 431–462.CrossRefGoogle Scholar
Saberi, A., Mahpeykar, M.R. & Teymourtash, A.R. 2019 Experimental measurement of radius of circular hydraulic jumps: effect of radius of convex target plate. Flow Meas. Instrum. 65, 274–279.CrossRefGoogle Scholar
Scholle, M., Marner, F. & Gaskell, P.H. 2019 Thin liquid film formation on hemispherical and conical substrate. Proc. Appl. Maths Mech. 19, e201900111.Google Scholar
Singha, S.B., Bhattacharjee, J.K. & Ray, A.K. 2005 Hydraulic jump in one-dimensional flow. Eur. Phys. J. B 48, 417–426.CrossRefGoogle Scholar
Strogatz, S.H. 2015 Nonlinear Dynamics and Chaos, 2nd edn. Perseus Books.Google Scholar
Symons, D.D. 2011 Integral methods for flow in a conical centrifuge. Chem. Engng Sci. 66, 3020–3029.CrossRefGoogle Scholar
Takagi, D. & Huppert, H.E. 2010 Flow and instability of thin films on a cylinder and sphere. J. Fluid Mech. 647, 221–238.CrossRefGoogle Scholar
Tani, I. 1949 Water jump in the boundary layer. J. Phys. Soc. Japan 4, 212–215.CrossRefGoogle Scholar
Wang, T., Faria, D., Stevens, L.J., Tan, J.S.C., Davidson, J.F & Wilson, D.I. 2013 Flow patterns and draining films created by horizontal and inclined coherent water jets impinging on vertical walls. Chem. Engng Sci. 102, 585–601.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2019 The role of gravity in the prediction of the circular hydraulic jump radius for high-viscosity liquids. J. Fluid Mech. 862, 128–161.CrossRefGoogle Scholar
Wang, Y. & Khayat, R.E. 2021 The effects of gravity and surface tension on the circular hydraulic jump for low- and high-viscosity liquids: a numerical investigation. Phys. Fluids 33, 012105.CrossRefGoogle Scholar
Watanabe, S., Putkaradze, V. & Bohr, T. 2003 Integral methods for shallow free-surface flows with separation. J. Fluid Mech. 480, 233–265.CrossRefGoogle Scholar
Watson, E.J. 1964 The radial spread of a liquid jet over a horizontal plate. J. Fluid Mech. 20, 481–499.CrossRefGoogle Scholar
Weinstein, S.J. & Ruschak, K.J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29–53.CrossRefGoogle Scholar
Xue, N. & Stone, H.A. 2021 Draining and spreading along geometries that cause converging flows: viscous gravity currents on a downward-pointing cone and a bowl-shaped hemisphere. Phys. Rev. Fluids 6, 043801.CrossRefGoogle Scholar
Yeckel, A., Middleman, S. & Klumb, L.A. 1990 The removal of thin liquid films from periodically grooved surfaces by an impinging jet. Chem. Engng Commun. 96, 69–79.CrossRefGoogle Scholar
Yiantsios, S.G. & Higgins, B.G. 1989 Rayleigh–Taylor instability in thin viscous films. Phys. Fluids A1, 1484–1501.CrossRefGoogle Scholar
Zhou, G. & Prosperetti, A. 2020 A numerical study of mass transfer from laminar liquid films. J. Fluid Mech. 902, A10.CrossRefGoogle Scholar
Zhou, G. & Prosperetti, A. 2022 Dripping instability of a two-dimensional liquid film under an inclined plate. J. Fluid Mech. 932, A49.CrossRefGoogle Scholar
Zollars, R.L. & Krantz, W.B. 1976 Laminar film flow down a right circular cone. Ind. Engng Chem. Fundam. 15, 91–94.CrossRefGoogle Scholar
Zollars, R.L. & Krantz, W.B. 1980 Non-parallel flow effects on the stability of film flow down a right circular cone. J. Fluid Mech. 96, 585–601.CrossRefGoogle Scholar

Zhou and Prosperetti supplementary movie 1

See pdf file for movie caption

Download Zhou and Prosperetti supplementary movie 1(Video)
Video 197.3 KB

Zhou and Prosperetti supplementary movie 2

See pdf file for movie caption

Download Zhou and Prosperetti supplementary movie 2(Video)
Video 65.3 KB

Zhou and Prosperetti supplementary movie 3

See pdf file for movie caption

Download Zhou and Prosperetti supplementary movie 3(Video)
Video 59.9 KB

Zhou and Prosperetti supplementary movie 4

See pdf file for movie caption

Download Zhou and Prosperetti supplementary movie 4(Video)
Video 65 KB

Zhou and Prosperetti supplementary movie 5

See pdf file for movie caption

Download Zhou and Prosperetti supplementary movie 5(Video)
Video 197.5 KB
Supplementary material: PDF

Zhou and Prosperetti supplementary material

Captions for movies 1-5

Download Zhou and Prosperetti supplementary material(PDF)
PDF 562.8 KB