Article contents
Hydraulic jumps in a shallow flow down a slightly inclined substrate
Published online by Cambridge University Press: 30 September 2015
Abstract
This work examines free-surface flows down an inclined substrate. The slope of the free surface and that of the substrate are both assumed small, whereas the Reynolds number 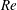 $Re$ remains unrestricted. A set of asymptotic equations is derived, which includes the lubrication and shallow-water approximations as limiting cases (as
$Re$ remains unrestricted. A set of asymptotic equations is derived, which includes the lubrication and shallow-water approximations as limiting cases (as  $Re\rightarrow 0$ and
$Re\rightarrow 0$ and 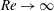 $Re\rightarrow \infty$ , respectively). The set is used to examine hydraulic jumps (bores) in a two-dimensional flow down an inclined substrate. An existence criterion for steadily propagating bores is obtained for the
$Re\rightarrow \infty$ , respectively). The set is used to examine hydraulic jumps (bores) in a two-dimensional flow down an inclined substrate. An existence criterion for steadily propagating bores is obtained for the 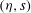 $({\it\eta},s)$ parameter space, where
$({\it\eta},s)$ parameter space, where 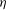 ${\it\eta}$ is the bore’s downstream-to-upstream depth ratio, and
${\it\eta}$ is the bore’s downstream-to-upstream depth ratio, and  $s$ is a non-dimensional parameter characterising the substrate’s slope. The criterion reflects two different mechanisms restricting bores. If
$s$ is a non-dimensional parameter characterising the substrate’s slope. The criterion reflects two different mechanisms restricting bores. If  $s$ is sufficiently large, a ‘corner’ develops at the foot of the bore’s front – which, physically, causes overturning. If, in turn,
$s$ is sufficiently large, a ‘corner’ develops at the foot of the bore’s front – which, physically, causes overturning. If, in turn, 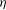 ${\it\eta}$ is sufficiently small (i.e. the bore’s relative amplitude is sufficiently large), the non-existence of bores is caused by a stagnation point emerging in the flow.
${\it\eta}$ is sufficiently small (i.e. the bore’s relative amplitude is sufficiently large), the non-existence of bores is caused by a stagnation point emerging in the flow.
Information
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 10
- Cited by


