Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T21:00:27.104Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydrodynamic diffusion in active microrheology of non-colloidal suspensions: the role of interparticle forces

Published online by Cambridge University Press:  16 November 2015

N. J. Hoh  and
R. N. Zia
N. J. Hoh
Affiliation:
School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
R. N. Zia*
Affiliation:
School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: zia@cbe.cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Hydrodynamic diffusion in the absence of Brownian motion is studied via active microrheology in the ‘pure-hydrodynamic’ limit, with a view towards elucidating the transition from colloidal microrheology to the non-colloidal limit, falling-ball rheometry. The phenomenon of non-Brownian force-induced diffusion in falling-ball rheometry is strictly hydrodynamic in nature; in contrast, analogous force-induced diffusion in colloids is deeply connected to the presence of a diffusive boundary layer even when Brownian motion is very weak compared with the external force driving the ‘probe’ particle. To connect these two limits, we derive an expression for the force-induced diffusion in active microrheology of hydrodynamically interacting particles via the Smoluchowski equation, where thermal fluctuations play no role. While it is well known that the microstructure is spherically symmetric about the probe in this limit, fluctuations in the microstructure need not be – and indeed lead to a diffusive spread of the probe trajectory. The force-induced diffusion is anisotropic, with components along and transverse to the line of external force. The latter is identically zero owing to the fore–aft symmetry of pair trajectories in Stokes flow. In a naïve first approach, the vanishing relative hydrodynamic mobility at contact between the probe and an interacting bath particle was assumed to eliminate all physical contribution from interparticle forces, whereby advection alone drove structural evolution in pair density and microstructural fluctuations. With such an approach, longitudinal force-induced diffusion vanishes in the absence of Brownian motion, a result that contradicts well-known experimental measurements of such diffusion in falling-ball rheometry. To resolve this contradiction, the probe–bath-particle interaction at contact was carefully modelled via an excluded annulus. We find that interparticle forces play a crucial role in encounters between particles in the hydrodynamic limit – as they must, to balance the advective flux. Accounting for this force results in a longitudinal force-induced diffusion 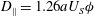$D_{\Vert }=1.26aU_{S}{\it\phi}$, where $a$ is the probe size, 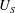$U_{S}$ is the Stokes velocity and 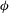${\it\phi}$ is the volume fraction of bath particles, in excellent qualitative and quantitative agreement with experimental measurements in, and theoretical predictions for, macroscopic falling-ball rheometry. This new model thus provides a continuous connection between micro- and macroscale rheology, as well as providing important insight into the role of interparticle forces for diffusion and rheology even in the limit of pure hydrodynamics: interparticle forces give rise to non-Newtonian rheology in strongly forced suspensions. A connection is made between the flow-induced diffusivity and the intrinsic hydrodynamic microviscosity which recovers a precise balance between fluctuation and dissipation in far from equilibrium suspensions; that is, diffusion and drag arise from a common microstructural origin even far from equilibrium.

JFM classification

Complex Fluids: Complex Fluids Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 785 , 25 December 2015 , pp. 189 - 218
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbott, J. R., Graham, A. L., Mondy, L. A. & Brenner, H. 1998 Dispersion of a ball settling through a quiescent neutrally buoyant suspension. J. Fluid Mech. 361, 309–331.CrossRefGoogle Scholar
Acrivos, A., Batchelor, G. K., Hinch, E. J., Koch, D. L. & Mauri, R. 1992 Longitudinal shear-induced diffusion of spheres in a dilute suspension. J. Fluid Mech. 240, 651–657.Google Scholar
Almog, Y. & Brenner, H. 1997 Non-continuum anomalies in the apparent viscosity experienced by a test sphere moving through an otherwise quiescent suspension. Phys. Fluids 9, 16–22.Google Scholar
Batchelor, G. K. 1976 Brownian diffusion of particles with hydrodynamic interaction. J. Fluid Mech. 74, 1–29.Google Scholar
Batchelor, G. K. 1982 Sedimentation in a dilute polydisperse system of interacting spheres. Part 1. General theory. J. Fluid Mech. 119, 379–408.Google Scholar
Batchelor, G. K. & Green, J. T. 1972 The determination of the bulk stress in a suspension of spherical particles to order $c^{2}$ . J. Fluid Mech. 56, 401–427.Google Scholar
Batchelor, G. K. & Wen, C.-S. 1982 Sedimentation in a dilute polydisperse system of interacting spheres. Part 2. Numerical results. J. Fluid Mech. 124, 495–528.Google Scholar
Beimfohr, S., Looby, T. & Leighton, D. T. 1993 Measurement of the shear-induced coefficient of self-diffusion in dilute suspensions. In Proceedings of the DOE/NSF Workshop on Flow of Particles and Fluids (ed. Plasynski, S. I., Peters, W. C. & Roco, M. C.), National Technical Information Service.Google Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 103–139.Google Scholar
da Cunha, F. R. & Hinch, E. J. 1996 Shear-induced dispersion in a dilute suspension of rough spheres. J. Fluid Mech. 309, 211–223.Google Scholar
Davis, R. H. 1992 Effects of surface roughness on a sphere sedimenting through a dilute suspension of neutrally buoyant spheres. Phys. Fluids A 4, 2607–2619.Google Scholar
Davis, R. H. & Hill, N. A. 1992 Hydrodynamic diffusion of a sphere settling through a dilute suspension of neutrally buoyant spheres. J. Fluid Mech. 236, 513–533.Google Scholar
Eckstein, E. C., Bailey, D. G. & Shapiro, A. H. 1977 Self-diffusion of particles in shear flow of a suspension. J. Fluid Mech. 79, 191–208.Google Scholar
Gadala-Maria, F. & Acrivos, A. 1980 Shear-induced structure in a concentrated suspension of solid spheres. J. Rheol. 24, 799–814.Google Scholar
Ham, J. M. & Homsy, G. M. 1988 Hindered settling and hydrodynamic dispersion in quiescent sedimenting suspensions. Intl J. Multiphase Flow 14, 533–546.Google Scholar
Ho, B. P. & Leal, L. G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 65, 365–400.CrossRefGoogle Scholar
Jeffrey, D. J. & Onishi, Y. 1984 Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 139, 261–290.Google Scholar
Khair, A. S. & Brady, J. F. 2006 Single particle motion in colloidal dispersions: a simple model for active and nonlinear microrheology. J. Fluid Mech. 557, 73–117.Google Scholar
Kim, S. & Karrila, S. J. 2005 Microhydrodynamics: Principles and Selected Applications. Dover.Google Scholar
Koch, D. L. & Shaqfeh, E. S. G. 1991 Screening in sedimenting suspensions. J. Fluid Mech. 224, 275–303.Google Scholar
Leighton, D. & Acrivos, A. 1987a Measurement of shear-induced self-diffusion in concentrated suspensions of spheres. J. Fluid Mech. 177, 109–131.CrossRefGoogle Scholar
Leighton, D. & Acrivos, A. 1987b The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.Google Scholar
Milliken, W., Mondy, L. A., Gottlieb, M., Graham, A. L. & Powell, R. L. 1989 The effect of the diameter of falling balls on the apparent viscosity of suspensions of spheres and rods. Phys. Chem. Hydrodyn. 11, 341–355.Google Scholar
Nicolai, H. & Guazzelli, É. 1995 Effect of the vessel size on the hydrodynamic diffusion of sedimenting spheres. Phys. Fluids 7, 3–5.Google Scholar
Nicolai, H., Herzhaft, B., Hinch, E. J., Oger, L. & Guazzelli, E. 1995 Particle velocity fluctuations and hydrodynamic self-diffusion of sedimenting non-Brownian spheres. Phys. Fluids 7, 12–23.CrossRefGoogle Scholar
Nicolai, H., Peysson, Y. & Guazzelli, É. 1996 Velocity fluctuations of a heavy sphere falling through a sedimenting suspension. Phys. Fluids 8, 855–862.Google Scholar
Russel, W. B. 1984 The Huggins coefficient as a means for characterizing suspended particles. J. Chem. Soc. Faraday Trans. 2 80, 31–41.CrossRefGoogle Scholar
Segré, G. & Silberberg, A. 1961 Radial particle displacements in Poiseuille flow of suspensions. Nature 189, 209–210.Google Scholar
Squires, T. M. & Brady, J. F. 2005 A simple paradigm for active and nonlinear microrheology. Phys. Fluids 17, 073101.Google Scholar
Swan, J. W. & Zia, R. N. 2013 Active microrheology: fixed-velocity versus fixed-force. Phys. Fluids 25, 083303.Google Scholar
Zia, R. N. & Brady, J. F. 2010 Single-particle motion in colloids: force-induced diffusion. J. Fluid Mech. 658, 188–210.Google Scholar
Zia, R. N. & Brady, J. F. 2012 Microviscosity, microdiffusivity, and normal stresses in colloidal dispersions. J. Rheol. 56, 1175–1208.Google Scholar
Zia, R. N. & Brady, J. F. 2013 Stress development, relaxation, and memory in colloidal dispersions: transient nonlinear microrheology. J. Rheol. 57, 457–492.CrossRefGoogle Scholar