Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T06:11:44.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydrodynamic interactions between aerosol particles in the transition regime

Published online by Cambridge University Press:  19 September 2018

James Corson Open the ORCID record for James Corson [Opens in a new window] ,
G. W. Mulholland  and
M. R. Zachariah
James Corson
Affiliation:
Department of Chemical and Biomolecular Engineering, University of Maryland, College Park, MD 20742, USA
G. W. Mulholland
Affiliation:
Department of Chemical and Biomolecular Engineering, University of Maryland, College Park, MD 20742, USA
M. R. Zachariah*
Affiliation:
Department of Chemical and Biomolecular Engineering, University of Maryland, College Park, MD 20742, USA Department of Chemistry and Biochemistry, University of Maryland, College Park, MD 20742, USA
*
†Email address for correspondence: mrz@umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a method for calculating the hydrodynamic interactions between particles in the kinetic (or transition regime), characterized by non-negligible particle Knudsen numbers. Such particles are often present in aerosol systems. The method is based on our extended Kirkwood–Riseman theory (Corson et al., Phys. Rev. E, vol. 95 (1), 2017c, 013103), which accounts for interactions between spheres using the velocity field around a translating sphere as a function of Knudsen number. Results for the two-sphere problem at small Knudsen numbers are in good agreement with those obtained using Felderhof’s interaction actions for mixed slip-stick boundary conditions, which are accurate to order 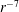$r^{-7}$ (Felderhof, Physica A, vol. 89 (2), 1977, pp. 373–384). The strength of the interactions decreases with increasing Knudsen number. Results for two fractal aggregates demonstrate that one can apply a point force approach for interactions between particles in the transition regime; the interaction tensor is similar to the Oseen tensor for continuum flow. Using this point force approach, we present an analysis for the settling of an unbounded cloud of particles. Our analysis shows that for sufficiently high volume fractions and cloud radii, the cloud behaves as a gas droplet in continuum flow even when the individual particles are small relative to the mean free path of the gas. The method presented here can be applied in a Brownian dynamics simulation analogous to Stokesian dynamics to study the behaviour of a dense aerosol system.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Rarefied Gas Flow: Rarefied Gas Flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 535 - 553
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1972 Sedimentation in a dilute dispersion of spheres. J. Fluid Mech. 52 (2), 245–268.Google Scholar
Batchelor, G. K. 1976 Brownian diffusion of particles with hydrodynamic interaction. J. Fluid Mech. 74 (1), 1–29.Google Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. Part I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511–525.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20 (1), 111–157.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3–4), 242–251.Google Scholar
Brenner, H. 1967 Coupling between the translational and rotational Brownian motions of rigid particles of arbitrary shape. Part II. General theory. J. Colloid Interface Sci. 23 (3), 407–436.Google Scholar
Burgers, J. M. 1995 Hydrodynamics on the influence of the concentration of a suspension upon the sedimentation velocity (in particular for a suspension of spherical particles). In Selected Papers of J. M. Burgers, pp. 452–477. Springer.Google Scholar
Carrasco, B. & García de la Torre, J. 1999 Improved hydrodynamic interaction in macromolecular bead models. J. Chem. Phys. 111 (10), 4817–4826.Google Scholar
Chen, Z.-Y., Deutch, J. M. & Meakin, P. 1984 Translational friction coefficient of diffusion limited aggregates. J. Chem. Phys. 80 (6), 2982–2983.Google Scholar
Corson, J., Mulholland, G. W. & Zachariah, M. R. 2017a Analytical expression for the friction coefficient of DLCA aggregates based on extended Kirkwood–Riseman theory. Aerosol Sci. Technol. 51 (6), 766–777.Google Scholar
Corson, J., Mulholland, G. W. & Zachariah, M. R. 2017b Calculating the rotational friction coefficient of fractal aerosol particles in the transition regime using extended Kirkwood–Riseman theory. Phys. Rev. E 96 (1), 013110.Google Scholar
Corson, J., Mulholland, G. W. & Zachariah, M. R. 2017c Friction factor for aerosol fractal aggregates over the entire Knudsen range. Phys. Rev. E 95 (1), 013103.Google Scholar
Corson, J., Mulholland, G. W. & Zachariah, M. R. 2018a Analytical expression for the rotational friction coefficient of DLCA aggregates over the entire Knudsen regime. Aerosol Sci. Technol. 52 (2), 209–221.Google Scholar
Corson, J., Mulholland, G. W. & Zachariah, M. R. 2018b The effect of electric field induced alignment on the electrical mobility of fractal aggregates. Aerosol Sci. Technol. 52 (5), 524–535.Google Scholar
Dahneke, B. E. 1973 Slip correction factors for nonspherical bodies. Part III. The form of the general law. J. Aero. Sci. 4 (2), 163–170.Google Scholar
Ermak, D. L. & McCammon, J. A. 1978 Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 69 (4), 1352–1360.Google Scholar
Felderhof, B. U. 1977 Hydrodynamic interaction between two spheres. Physica A 89 (2), 373–384.Google Scholar
Friedlander, S. K. 2000 Smoke, Dust, and Haze: Fundamentals of Aerosol Dynamics, 2nd edn. Topics in Chemical Engineering, vol. 2. Oxford University Press.Google Scholar
Fuchs, N. A. 1964 The Mechanics of Aerosols. Pergamon Press.Google Scholar
Goldman, A. J., Cox, R. G. & Brenner, H. 1966 The slow motion of two identical arbitrarily oriented spheres through a viscous fluid. Chem. Engng Sci. 21 (12), 1151–1170.Google Scholar
Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Media, Prentice Hall International Series in the Physical and Chemical Engineering Sciences, vol. 1. Prentice Hall.Google Scholar
Heine, M. C. & Pratsinis, S. E. 2007 Brownian coagulation at high concentration. Langmuir 23 (19), 9882–9890.Google Scholar
Heinson, W. R., Pierce, F., Sorensen, C. M. & Chakrabarti, A. 2014 Crossover from ballistic to Epstein diffusion in the free-molecular regime. Aerosol Sci. Technol. 48 (7), 738–746.Google Scholar
Kirkwood, J. G. & Riseman, J. 1948 The intrinsic viscosities and diffusion constants of flexible macromolecules in solution. J. Chem. Phys. 16 (6), 565–573.Google Scholar
Kogan, M. N. 1958 On the equations of motion of a rarefied gas. Z. Angew. Math. Mech. J. Appl. Math. Mech. 22 (4), 597–607.Google Scholar
Lattuada, M. 2011 Predictive model for diffusion-limited aggregation kinetics of nanocolloids under high concentration. J. Phys. Chem. B 116 (1), 120–129.Google Scholar
Lattuada, M., Wu, H. & Morbidelli, M. 2003 Hydrodynamic radius of fractal clusters. J. Colloid Interface Sci. 268 (1), 96–105.Google Scholar
Li, M., Mulholland, G. W. & Zachariah, M. R. 2014 Understanding the mobility of nonspherical particles in the free molecular regime. Phys. Rev. E 89 (2), 022112.Google Scholar
Loyalka, S. K. 1990 Slip and jump coefficients for rarefied gas flows: variational results for Lennard-Jones and n (r)-6 potentials. Physica A 163 (3), 813–821.Google Scholar
Loyalka, S. K. 1992 Motion of a sphere in a gas: numerical solution of the linearized Boltzmann equation. Phys. Fluids A 4 (5), 1049–1056.Google Scholar
Mackaplow, M. B. & Shaqfeh, E. S. G. 1998 A numerical study of the sedimentation of fibre suspensions. J. Fluid Mech. 376, 149–182.Google Scholar
Mackowski, D. W. 2006 Monte Carlo simulation of hydrodynamic drag and thermophoresis of fractal aggregates of spheres in the free-molecule flow regime. J. Aero. Sci. 37 (3), 242–259.Google Scholar
Matsuoka, Y., Fukasawa, T., Higashitani, K. & Yamamoto, R. 2012 Effect of hydrodynamic interactions on rapid Brownian coagulation of colloidal dispersions. Phys. Rev. E 86 (5), 051403.Google Scholar
Mazur, P. & Van Saarloos, W. 1982 Many-sphere hydrodynamic interactions and mobilities in a suspension. Physica A 115 (1–2), 21–57.Google Scholar
Mountain, R. D., Mulholland, G. W. & Baum, H. 1986 Simulation of aerosol agglomeration in the free molecular and continuum flow regimes. J. Colloid Interface Sci. 114 (1), 67–81.Google Scholar
Pratsinis, S. E. 1998 Flame aerosol synthesis of ceramic powders. Prog. Energy Combust. Sci. 24 (3), 197–219.Google Scholar
Rotne, J. & Prager, S. 1969 Variational treatment of hydrodynamic interaction in polymers. J. Chem. Phys. 50 (11), 4831–4837.Google Scholar
Smoluchowski, M. 1912 On the Practical Applicability of Stokes’ Law of Resistance, and the Modifications of it Required in Certain Cases. Proc. 5th Intern. Cong. Math., vol. 2, p. 192.Google Scholar
Sorensen, C. M. 2011 The mobility of fractal aggregates: a review. Aerosol Sci. Technol. 45 (7), 765–779.Google Scholar
Sorensen, C. M. & Chakrabarti, A. 2011 The sol to gel transition in irreversible particulate systems. Soft Matt. 7 (6), 2284–2296.Google Scholar
Sorensen, C. M., Hageman, W. B., Rush, T. J., Huang, H. & Oh, C. 1998 Aerogelation in a flame soot aerosol. Phys. Rev. Lett. 80 (8), 1782–1785.Google Scholar
Stimson, M. & Jeffery, G. B. 1926 The motion of two spheres in a viscous fluid. Proc. R. Soc. Lond. A 111 (757), 110–116.Google Scholar
Takata, S., Sone, Y. & Aoki, K. 1993 Numerical analysis of a uniform flow of a rarefied gas past a sphere on the basis of the Boltzmann equation for hard-sphere molecules. Phys. Fluids A 5 (3), 716–737.Google Scholar
García de la Torre, J. & Rodes, V. 1983 Effects from bead size and hydrodynamic interactions on the translational and rotational coefficients of macromolecular bead models. J. Chem. Phys. 79 (5), 2454–2460.Google Scholar
Yamakawa, H. 1970 Transport properties of polymer chains in dilute solution: hydrodynamic interaction. J. Chem. Phys. 53 (1), 436–443.Google Scholar
Zhang, C., Thajudeen, T., Larriba, C., Schwartzentruber, T. E. & Hogan, C. J. Jr 2012 Determination of the scalar friction factor for nonspherical particles and aggregates across the entire Knudsen number range by direct simulation Monte Carlo (DSMC). Aerosol Sci. Technol. 46 (10), 1065–1078.Google Scholar