Article contents
Impact of compliant coating on Mack-mode evolution in hypersonic boundary layers
Published online by Cambridge University Press: 23 October 2023
Abstract
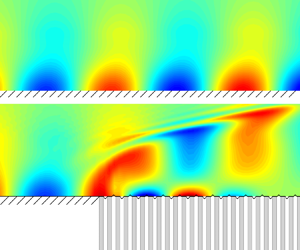
This paper focuses on the linear evolution of Mack instability modes in a hypersonic boundary layer over a flat plate that is partially coated by a compliant section. The compliant section is a thin, flexible membrane covering on a porous wall consisting of micro holes. The instability pressure could induce a vibration of the membrane, leading to a feedback to the boundary-layer fluids through the transverse velocity fluctuation. Such a process is formulated by an admittance boundary condition for the boundary-layer perturbation, which is dependent on the thickness and tension of the membrane, the properties of the porous wall, and the frequency of the Mack-mode perturbation. Using this admittance condition, the impact of the compliant coating on the Mack growth rate is studied systematically by solving the compressible Orr–Sommerfeld equations. It is found that the compliant coating could suppress the Mack instability with a frequency band in the neighbourhood of the most unstable frequency, and the stabilising frequency band widens as the membrane thickness and tension decrease, indicating a more favourable effect of a softer membrane. For a Mack mode with a specified dimensional frequency – since its dimensionless frequency, normalised by the local boundary-layer thickness and oncoming velocity, increases as it propagates downstream – the second-mode frequency band usually appears in downstream locations, and so does the stabilising effect of the membrane. Thus it is favourable to apply a compliant panel at a downstream region. In this situation, the solid–compliant junction could produce an additional scattering effect on the evolution of the Mack mode due to the sudden change of its boundary condition. The scattering effect is quantified by a transmission coefficient defined by the equivalent amplitude of the compliant-wall perturbation to the solid-wall perturbation, which can be obtained by the harmonic linearised Navier–Stokes (HLNS) approach. If the admittance is weak, then the transmission coefficient can also be predicted by an analytical solution based on the residue theorem. It is found that most of the second modes are suppressed by the scattering effect as long as the argument of the admittance is in the interval  $[150^\circ, 210^\circ ]$, agreeing with most of the physical situation. The analytical predictions agree well with the HLNS calculations when the modulus of the admittance is less than
$[150^\circ, 210^\circ ]$, agreeing with most of the physical situation. The analytical predictions agree well with the HLNS calculations when the modulus of the admittance is less than  $O(0.1)$.
$O(0.1)$.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 4
- Cited by


