Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-12T23:53:30.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of inlet gas turbulence on the formation, development and breakup of interfacial waves in a two-phase mixing layer

Published online by Cambridge University Press:  29 June 2021

D. Jiang  and
Y. Ling Open the ORCID record for Y. Ling [Opens in a new window]
D. Jiang
Affiliation:
Department of Mechanical Engineering, Baylor University, Waco, TX76798, USA
Y. Ling*
Affiliation:
Department of Mechanical Engineering, Baylor University, Waco, TX76798, USA
*
†Email address for correspondence: stanley_ling@baylor.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

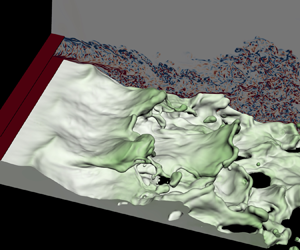
Understanding the development and breakup of interfacial waves in a two-phase mixing layer between the gas and liquid streams is paramount to atomization. Due to the velocity difference between the two streams, the shear on the interface triggers a longitudinal instability, which develops to interfacial waves that propagate downstream. As the interfacial waves grow spatially, transverse modulations arise, turning the interfacial waves from quasi-two-dimensional to fully three-dimensional. The inlet gas turbulence intensity has a strong impact on the interfacial instability. Therefore, parametric direct numerical simulations are performed in the present study to systematically investigate the effect of the inlet gas turbulence on the formation, development and breakup of the interfacial waves. The open-source multiphase flow solver, PARIS, is used for the simulations and the mass–momentum consistent volume-of-fluid method is used to capture the sharp gas–liquid interfaces. Two computational domain widths are considered and the wide domain will allow a detailed study of the transverse development of the interfacial waves. The dominant frequency and spatial growth rate of the longitudinal instability are found to increase with the inlet gas turbulence intensity. The dominant transverse wavenumber, determined by the Rayleigh–Taylor instability, scales with the longitudinal frequency, so it also increases with the inlet gas turbulence intensity. The holes formed in the liquid sheet are important to the disintegration of the interfacial waves. The hole formation is influenced by the inlet gas turbulence. As a result, the sheet breakup dynamics and the statistics of the droplets formed also change accordingly.

JFM classification

Multiphase and Particle-laden Flows: Gas/liquid flow Waves/Free-surface Flows: Wind-wave interactions Drops and Bubbles: Aerosols/atomization
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 921 , 25 August 2021 , A15
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agbaglah, G., Chiodi, R. & Desjardins, O. 2017 Numerical simulation of the initial destabilization of an air-blasted liquid layer. J. Fluid Mech. 812, 1024–1038.CrossRefGoogle Scholar
Agbaglah, G., Josserand, C. & Zaleski, S. 2013 Longitudinal instability of a liquid rim. Phys. Fluids 25, 022103.CrossRefGoogle Scholar
Agbaglah, G.G. 2021 Breakup of thin liquid sheets through hole–hole and hole–rim merging. J. Fluid Mech. 911, A23.CrossRefGoogle Scholar
Ambravaneswaran, B., Wilkes, E.D. & Basaran, O.A. 2002 Drop formation from a capillary tube: comparison of one-dimensional and two-dimensional analyses and occurrence of satellite drops. Phys. Fluids 14, 2606–2621.CrossRefGoogle Scholar
Aniszewski, W., et al. 2021 Parallel, robust, interface simulator (PARIS). Comput. Phys. Commun. 263, 107849.CrossRefGoogle Scholar
Arrufat, T., Crialesi-Esposito, M., Fuster, D., Ling, Y., Malan, L., Pal, S., Scardovelli, R., Tryggvason, G. & Zaleski, S. 2020 A momentum-conserving, consistent, volume-of-fluid method for incompressible flow on staggered grids. Comput. Fluids 215, 104785.CrossRefGoogle Scholar
Aulisa, E., Manservisi, S., Scardovelli, R. & Zaleski, S. 2007 Interface reconstruction with least-squares fit and split advection in three-dimensional cartesian geometry. J. Comput. Phys. 225, 2301–2319.CrossRefGoogle Scholar
Balachandar, S., Zaleski, S., Soldati, A., Ahmadi, G. & Bourouiba, L. 2020 Host-to-host airborne transmission as a multiphase flow problem for science-based social distance guidelines. Intl J. Multiphase Flow 132, 103439.CrossRefGoogle Scholar
Boeck, T. & Zaleski, S. 2005 Viscous versus inviscid instability of two-phase mixing layers with continuous velocity profile. Phys. Fluids 17, 032106.CrossRefGoogle Scholar
Castrejón-Pita, J.R., Castrejón-Pita, A.A., Thete, S.S., Sambath, K., Hutchings, I.M., Hinch, J., Lister, J.R. & Basaran, O.A. 2015 Plethora of transitions during breakup of liquid filaments. Proc. Natl Acad. Sci. USA 112, 4582–4587.CrossRefGoogle ScholarPubMed
Chandrasekhar, S. 1961 Hydrodynamic and hydromagnetic stability. Oxford University Press.Google Scholar
Chaussonnet, G., Gepperth, S., Holz, S., Koch, R. & Bauer, H.-J. 2020 Influence of the ambient pressure on the liquid accumulation and on the primary spray in prefilming airblast atomization. Intl J. Multiphase Flow 125, 103229.CrossRefGoogle Scholar
Chorin, A.J. 1968 Numerical solution of the Navier–Stokes equations. Math. Comput. 22, 745–762.CrossRefGoogle Scholar
Delon, A., Cartellier, A. & Matas, J.-P. 2018 Flapping instability of a liquid jet. Phys. Rev. Fluids 3, 043901.CrossRefGoogle Scholar
Dimotakis, P.E. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24, 1791–1796.CrossRefGoogle Scholar
Duguid, J.P. 1946 The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. Epidemiol. Infect. 44, 471–479.CrossRefGoogle ScholarPubMed
Eggers, J. 1993 Universal pinching of 3D axisymmetric free-surface flow. Phys. Rev. Lett. 71, 3458.CrossRefGoogle ScholarPubMed
Francois, M.M., Cummins, S.J., Dendy, E.D., Kothe, D.B., Sicilian, J.M. & Williams, M.W. 2006 A balanced-force algorithm for continuous and sharp interfacial surface tension models within a volume tracking framework. J. Comput. Phys. 213, 141–173.CrossRefGoogle Scholar
Fuster, D., Matas, J.P., Marty, S., Popinet, S., Hoepffner, J., Cartellier, A. & Zaleski, S. 2013 Instability regimes in the primary breakup region of planar coflowing sheets. J. Fluid Mech. 736, 150–176.CrossRefGoogle Scholar
Healey, J.J. 2007 Enhancing the absolute instability of a boundary layer by adding a far-away plate. J. Fluid Mech. 579, 29–61.CrossRefGoogle Scholar
Herrmann, M. 2011 The influence of density ratio on the primary atomization of a turbulent liquid jet in crossflow. Proc. Combust. Inst. 33, 2079–2088.CrossRefGoogle Scholar
Hoepffner, J., Blumenthal, R. & Zaleski, S. 2011 Self-similar wave produced by local perturbation of the Kelvin–Helmholtz shear-layer instability. Phys. Rev. Lett. 106, 104502.CrossRefGoogle ScholarPubMed
Jarrahbashi, D. & Sirignano, W.A. 2014 Vorticity dynamics for transient high-pressure liquid injection a. Phys. Fluids 26, 73.CrossRefGoogle Scholar
Jarrahbashi, D., Sirignano, W.A., Popov, P.P. & Hussain, F. 2016 Early spray development at high gas density: hole, ligament and bridge formations. J. Fluid Mech. 792, 186–231.CrossRefGoogle Scholar
Jiang, D. & Ling, Y. 2020 Destabilization of a planar liquid stream by a co-flowing turbulent gas stream. Intl J. Multiphase Flow 122, 103121.CrossRefGoogle Scholar
Joseph, D.D., Belanger, J. & Beavers, G.S. 1999 Breakup of a liquid drop suddenly exposed to a high-speed airstream. Intl J. Multiphase Flow 25, 1263–1303.CrossRefGoogle Scholar
Juniper, M.P 2006 The effect of confinement on the stability of two-dimensional shear flows. J. Fluid Mech. 565, 171–195.CrossRefGoogle Scholar
Klein, M., Sadiki, A. & Janicka, J. 2003 A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 186, 652–665.CrossRefGoogle Scholar
Kooij, S., Sijs, R., Denn, M.M., Villermaux, E. & Bonn, D. 2018 What determines the drop size in sprays? Phys. Rev. X 8, 031019.Google Scholar
Lasheras, J.C., Villermaux, E. & Hopfinger, E.J. 1998 Break-up and atomization of a round water jet by a high-speed annular air jet. J. Fluid Mech. 357, 351–379.CrossRefGoogle Scholar
Lefebvre, A. 1988 Atomization and sprays. CRC Press.CrossRefGoogle Scholar
Lefebvre, A.H. 1980 Airblast atomization. Prog. Energy Combust. Sci. 6, 233–261.CrossRefGoogle Scholar
Li, J. 1995 Calcul d'interface affine par morceaux (piecewise linear interface calculation). C. R. Acad. Sci. Paris (IIb) 320, 391–396.Google Scholar
Ling, Y., Fuster, D., Tryggvasson, G. & Zaleski, S. 2019 A two-phase mixing layer between parallel gas and liquid streams: multiphase turbulence statistics and influence of interfacial instability. J. Fluid Mech. 859, 268–307.CrossRefGoogle Scholar
Ling, Y., Fuster, D., Zaleski, S. & Tryggvason, G. 2017 Spray formation in a quasiplanar gas-liquid mixing layer at moderate density ratios: a numerical closeup. Phys. Rev. Fluids 2, 014005.CrossRefGoogle Scholar
Ling, Y., Zaleski, S. & Scardovelli, R. 2015 Multiscale simulation of atomization with small droplets represented by a lagrangian point-particle model. Intl J. Multiphase Flow 76, 122–143.CrossRefGoogle Scholar
Marmottant, P. & Villermaux, E. 2004 On spray formation. J. Fluid Mech. 498, 73–111.CrossRefGoogle Scholar
Marston, J.O., Truscott, T.T., Speirs, N.B., Mansoor, M.M. & Thoroddsen, S.T. 2016 Crown sealing and buckling instability during water entry of spheres. J. Fluid Mech. 794, 506–529.CrossRefGoogle Scholar
Marty, S. 2015 Contribution a l’étude de l'atomisation assistée d'un liquide. PhD thesis, Université de Grenoble.Google Scholar
Matas, J.-P. 2015 Inviscid versus viscous instability mechanism of an air–water mixing layer. J. Fluid Mech. 768, 375–387.CrossRefGoogle Scholar
Matas, J.-P., Delon, A. & Cartellier, A. 2018 Shear instability of an axisymmetric air–water coaxial jet. J. Fluid Mech. 843, 575–600.CrossRefGoogle Scholar
Matas, J.-P., Marty, S. & Cartellier, A. 2011 Experimental and analytical study of the shear instability of a gas-liquid mixing layer. Phys. Fluids 23, 094112.CrossRefGoogle Scholar
Matas, J.-P., Marty, S., Dem, M.S. & Cartellier, A. 2015 Influence of gas turbulence on the instability of an air-water mixing layer. Phys. Rev. Lett. 115, 074501.CrossRefGoogle ScholarPubMed
O'Naraigh, L., Spelt, P.D.M. & Shaw, S.J. 2013 Absolute linear instability in laminar and turbulent gas–liquid two-layer channel flow. J. Fluid Mech. 714, 58–94.CrossRefGoogle Scholar
Opfer, L., Roisman, I.V., Venzmer, J., Klostermann, M. & Tropea, C. 2014 Droplet-air collision dynamics: evolution of the film thickness. Phys. Rev. E 89, 013023.CrossRefGoogle ScholarPubMed
Otto, T., Rossi, M. & Boeck, T. 2013 Viscous instability of a sheared liquid-gas interface: dependence on fluid properties and basic velocity profile. Phys. Fluids 25, 032103.CrossRefGoogle Scholar
Popinet, S. 2009 An accurate adaptive solver for surface-tension-driven interfacial flows. J. Comput. Phys. 228 (16), 5838–5866.CrossRefGoogle Scholar
Raynal, L. 1997 Instabilite et entrainement a l'interface d'une couche de melange liquide-gaz. PhD thesis, Université Joseph Fourier - Grenoble I.Google Scholar
Renardy, Y. & Renardy, M. 2002 PROST: a parabolic reconstruction of surface tension for the volume-of-fluid method. J. Comput. Phys. 183, 400–421.CrossRefGoogle Scholar
Roisman, I.V. 2010 On the instability of a free viscous rim. J. Fluid Mech. 661, 206–228.CrossRefGoogle Scholar
Rudman, M. 1998 A volume-tracking method for incompressible multifluid flows with large density variations. Intl J. Numer. Meth. Fluids 28, 357–378.3.0.CO;2-D>CrossRefGoogle Scholar
Scardovelli, R. & Zaleski, S. 2003 Interface reconstruction with least-square fit and split Eulerian–Lagrangian advection. Intl J. Numer. Meth. Fluids 41 (3), 251–274.CrossRefGoogle Scholar
Simmons, H.C. 1977 a The correlation of drop-size distributions in fuel nozzle sprays: part I. The drop-size/volume-fraction distribution. J. Engng Power 7, 309–314.CrossRefGoogle Scholar
Simmons, H.C. 1977 b The correlation of drop-size distributions in fuel nozzle sprays: part II. The drop-size/number distribution. J. Engng Power 7, 315–319.CrossRefGoogle Scholar
Snoeijer, J.H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.CrossRefGoogle Scholar
Tryggvason, G., Scardovelli, R. & Zaleski, S. 2011 Direct numerical simulations of gas-liquid multiphase flows. Cambridge University Press.Google Scholar
Varga, C.M., Lasheras, J.C. & Hopfinger, E.J. 2003 Initial breakup of a small-diameter liquid jet by a high-speed gas stream. J. Fluid Mech. 497, 405–434.CrossRefGoogle Scholar
Vaudor, G., Ménard, T., Aniszewski, W., Doring, M. & Berlemont, A. 2017 A consistent mass and momentum flux computation method for two phase flows. Application to atomization process. Comput. Fluids 152, 204–216.CrossRefGoogle Scholar
Villermaux, E., Marmottant, P.. & Duplat, J. 2004 Ligament-mediated spray formation. Phys. Rev. Lett. 92, 074501.CrossRefGoogle ScholarPubMed
Zandian, A., Sirignano, W.A. & Hussain, F. 2018 Understanding liquid-jet atomization cascades via vortex dynamics. J. Fluid Mech. 843, 293–354.CrossRefGoogle Scholar
Zhang, B., Ling, Y., Tsai, P.-H., Wang, A.-B., Popinet, S. & Zaleski, S. 2019 Short-term oscillation and falling dynamics for a water drop dripping in quiescent air. Phys. Rev. Fluids 4, 123604.CrossRefGoogle Scholar
Zhang, B., Popinet, S. & Ling, Y. 2020 Modeling and detailed numerical simulation of the primary breakup of a gasoline surrogate jet under non-evaporative operating conditions. Intl J. Multiphase Flow 130, 103362.CrossRefGoogle Scholar

Jiang and Ling supplementary movie 1

Development of the interfacial waves in a two-phase mixing layer with a laminar gas inflow (left) and with a turbulent gas inflow (right). The color on the background of represents the velocity magnitude.

Download Jiang and Ling supplementary movie 1(Video)
Video 24.5 MB