Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T06:39:20.672Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertia–gravity waves in inertially stable and unstable shear flows

Published online by Cambridge University Press:  19 June 2015

François Lott ,
Christophe Millet  and
Jacques Vanneste
François Lott*
Affiliation:
Laboratoire de Météorologie Dynamique du CNRS, Ecole Normale Supérieure, 24, rue Lhomond, 75231 Paris CEDEX 05, France
Christophe Millet
Affiliation:
CEA, DAM, DIF, 91297 Arpajon, France
Jacques Vanneste
Affiliation:
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, Edinburgh EH9 3FD, UK
*
†Email address for correspondence: flott@lmd.ens.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

An inertia–gravity wave (IGW) propagating in a vertically sheared, rotating stratified fluid interacts with the pair of inertial levels that surround the critical level. An exact expression for the form of the IGW is derived here in the case of a linear shear and used to examine this interaction in detail. This expression recovers the classical values of the transmission and reflection coefficients 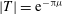$|T|=\text{e}^{-{\rm\pi}{\it\mu}}$ and 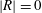$|R|=0$, where 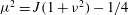${\it\mu}^{2}=J(1+{\it\nu}^{2})-1/4$, 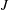$J$ is the Richardson number and ${\it\nu}$ the ratio between the horizontal transverse and along-shear wavenumbers. For large 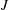$J$, a WKB analysis provides an interpretation of this result in term of tunnelling: an IGW incident on the lower inertial level becomes evanescent between the inertial levels, returning to an oscillatory behaviour above the upper inertial level. The amplitude of the transmitted wave is directly related to the decay of the evanescent solution between the inertial levels. In the immediate vicinity of the critical level, the evanescent IGW is well represented by the quasi-geostrophic approximation, so that the process can be interpreted as resulting from the coupling between balanced and unbalanced motion. The exact and WKB solutions describe the so-called valve effect, a dependence of the behaviour in the region between the inertial levels on the direction of wave propagation. For 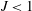$J<1$ this is shown to lead to an amplification of the wave between the inertial levels. Since the flow is inertially unstable for 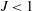$J<1$, this establishes a correspondence between the inertial-level interaction and the condition for inertial instability.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 775 , 25 July 2015 , pp. 223 - 240
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ablowitz, M. J. & Fokas, A. S. 1997 Complex Variables: Introduction and Applications. Cambridge University Press.Google Scholar
Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions, 9th edn. Dover.Google Scholar
Alford, M. H. 2003 Redistribution of energy available for ocean mixing by long-range propagation of internal waves. Nature 423, 159–162.CrossRefGoogle ScholarPubMed
Andrews, D. G., Holton, J. R. & Leovy, C. B. 1987 Middle Atmosphere Dynamics. Academic.Google Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Bennetts, D. A. & Hoskins, B. J. 1979 Conditional symmetric instability – a possible explanation for frontal rainbands. Q. J. R. Meteorol. Soc. 105, 945–962.Google Scholar
Booker, J. R. & Bretherton, F. P. 1967 The critical layer for internal gravity waves in a shear flow. J. Fluid Mech. 27, 513–539.CrossRefGoogle Scholar
Eliassen, A. & Palm, E. 1961 On the transfer of energy in stationary mountain waves. Geophys. Publ. 22, 1–23.Google Scholar
Ferrari, R. & Wunsch, C. 2009 Ocean circulation kinetic energy: reservoirs, sources and sinks. Annu. Rev. Fluid Mech. 41, 253–282.CrossRefGoogle Scholar
Gill, A. 1982 Atmosphere-Ocean Dynamics. Academic.Google Scholar
Grimshaw, R. 1975 Internal gravity waves: critical layer absorption in a rotating fluid. J. Fluid Mech. 70, 287–304.CrossRefGoogle Scholar
Gula, J. & Zeitlin, V. 2010 Instabilities of buoyancy driven coastal currents and their nonlinear evolution in the two-layer rotating shallow water model. Part 1. Passive lower layer. J. Fluid Mech. 659, 69–93.CrossRefGoogle Scholar
Hertzog, A., Boccara, G., Vincent, R. A., Vial, F. & Cocquerez, P. 2008 Estimation of gravity wave momentum flux and phase speeds from quasi-Lagrangian stratospheric balloon flights. Part II: results from the Vorcore campaign in Antarctica. J. Atmos. Sci. 65, 3056–3070.CrossRefGoogle Scholar
Howard, L. H. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.CrossRefGoogle Scholar
Inverarity, G. W. & Shutts, G. J. 2000 A general, linearized vertical structure equation for the vertical velocity: properties, scalings and special cases. Q. J. R. Meteorol. Soc. 126, 2709–2724.CrossRefGoogle Scholar
Jones, W. L. 1967 Propagation of internal gravity waves in fluids with shear flow and rotation. J. Fluid Mech. 30, 439–448.CrossRefGoogle Scholar
Lindzen, R. S. 1988 Instability of plane parallel shear-flow (toward a mechanistic picture of how it works). Pure Appl. Geophys. 126, 103–121.CrossRefGoogle Scholar
Lott, F. 1997 The transient emission of propagating gravity waves by a stably stratified shear layer. Q. J. R. Meteorol. Soc. 123, 1603–1619.CrossRefGoogle Scholar
Lott, F. 2003 Large-scale flow response to short gravity waves breaking in a rotating shear flow. J. Atmos. Sci. 60, 1691–1704.2.0.CO;2>CrossRefGoogle Scholar
Lott, F., Kelder, H. & Teitelbaum, H. 1992 A transition from Kelvin–Helmholtz instabilities to propagating wave instabilities. Phys. Fluids A 4, 1990–1997.CrossRefGoogle Scholar
Lott, F., Plougonven, R. & Vanneste, J. 2010 Gravity waves generated by sheared potential-vorticity anomalies. J. Atmos. Sci. 67, 157–170.CrossRefGoogle Scholar
Lott, F., Plougonven, R. & Vanneste, J. 2012 Gravity waves generated by sheared three-dimensional potential vorticity anomalies. J. Atmos. Sci. 69, 2134–2151.CrossRefGoogle Scholar
Mamatsashvili, G. R., Avsarkisov, V. S., Chagelishvili, G. D., Chanishvili, R. G. & Kalashnik, M. V. 2010 Transient dynamics of nonsymmetric perturbations versus symmetric instability in baroclinic zonal shear flows. J. Atmos. Sci. 67, 2972–2989.CrossRefGoogle Scholar
Marshall, J., Ferrari, R., Forget, G., Maze, G., Andersson, A., Bates, N., Dewar, W., Doney, S., Fratantoni, D., Joyce, T., Straneo, F., Toole, J., Weller, R., Edson, J., Gregg, M., Kelly, K., Lozier, S., Palter, J., Lumpkin, R., Samelson, R., Skyllingstad, E., Silverthorne, K., Talley, L. & Thomas, L. 2009 The CLIMODE field campaign: observing the cycle of convection and restratification over the Gulf Stream. Bull. Am. Meteorol. Soc. 90, 1337–1350.Google Scholar
McWilliams, J. C. 2003 Diagnostic force balance and its limits. In Nonlinear Processes in Geophysical Fluid Dynamics (ed. Velasco Fuentes, O. U., Sheinbaum, J. & Ochoa, J.), pp. 287–304. Kluwer.CrossRefGoogle Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.CrossRefGoogle Scholar
Miyahara, S. 1981 A note on the behavior of waves around the inertio frequency. J. Meteorol. Soc. Japan 59, 902–905.CrossRefGoogle Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2005 Baroclinic instability and loss of balance. J. Phys. Oceanogr. 35, 1505–1517.CrossRefGoogle Scholar
Plougonven, R., Muraki, D. J. & Snyder, C. 2005 A baroclinic instability that couples balanced motions and gravity waves. J. Atmos. Sci. 62, 1545–1559.CrossRefGoogle Scholar
Plougonven, R. & Snyder, C. 2007 Inertia-gravity waves spontaneously generated by jets and fronts. Part I: different baroclinic life cycles. J. Atmos. Sci. 64, 2502–2520.CrossRefGoogle Scholar
Rabinovitch, A., Umurhan, O. M., Harnik, N., Lott, F. & Heifetz, E. 2011 Vorticity inversion and action-at-a-distance instability in stably stratified shear flow. J. Fluid Mech. 670, 301–325.CrossRefGoogle Scholar
Richter, J. H., Sassi, F. & Garcia, R. R. 2010 Toward a physically based gravity wave source parameterization in a general circulation model. J. Atmos. Sci. 67, 136–156.CrossRefGoogle Scholar
Sakai, S. 1989 Rossby–Kelvin instability: a new type of ageostrophic instability caused by a resonnance between Rossby waves and gravity waves. J. Fluid Mech. 202, 149–176.CrossRefGoogle Scholar
Sato, K. & Yoshiki, M. 2008 Gravity wave generation around the polar vortex in the stratosphere revealed by 3-hourly radiosonde observations at Syowa station. J. Atmos. Sci. 65, 3719–3735.CrossRefGoogle Scholar
Scavuzzo, C. M., Lamfri, M. A., Teitelbaum, H. & Lott, F. 1998 A study of the low frequency inertio-gravity waves observed during PYREX. J. Geophys. Res. D2 103, 1747–1758.CrossRefGoogle Scholar
Shen, B. W. & Lin, Y. L. 1999 Effects of critical levels on two-dimensional back-sheared flow over an isolated mountain ridge on an f plane. J. Atmos. Sci. 56, 3286–3302.2.0.CO;2>CrossRefGoogle Scholar
Shutts, G. J. 2003 Inertia–gravity wave and neutral Eady wave trains forced by directionally sheared flow over isolated hills. J. Atmos. Sci. 60, 593–606.2.0.CO;2>CrossRefGoogle Scholar
Stone, P. H. 1966 On non-geostrophic baroclinic instability. J. Atmos. Sci. 23, 390–400.2.0.CO;2>CrossRefGoogle Scholar
Sutyrin, G. G. 2008 Lack of balance in continuously stratified rotating flows. J. Fluid Mech. 615, 93–100.CrossRefGoogle Scholar
Vanneste, J. & Yavneh, I. 2007 Unbalanced instabilities of rapidly rotating stratified sheared flows. J. Fluid Mech. 584, 373–396.CrossRefGoogle Scholar
Whitt, D. B. & Thomas, L. N. 2013 Near-inertial waves in strongly baroclinic currents. J. Phys. Oceanogr. 43, 706–725.CrossRefGoogle Scholar
Yamanaka, M. D. & Tanaka, H. 1984 Propagation and breakdown of internal inertia-gravity waves near critical levels in the middle atmosphere. J. Meteorol. Soc. Japan 62, 1–17.CrossRefGoogle Scholar
Zuelicke, C. & Peters, D. 2008 Parameterization of strong stratospheric inertia-gravity waves forced by poleward-breaking Rossby waves. Mon. Weath. Rev. 136, 98–119.CrossRefGoogle Scholar