Article contents
Inertial migration of a sphere in plane Couette flow
Published online by Cambridge University Press: 19 December 2023
Abstract
We study the inertial migration of a torque-free neutrally buoyant sphere in wall-bounded plane Couette flow over a wide range of channel Reynolds numbers  $Re_c$ in the limit of small particle Reynolds number (
$Re_c$ in the limit of small particle Reynolds number ( $Re_p\ll 1$) and confinement ratio (
$Re_p\ll 1$) and confinement ratio ( $\lambda \ll 1$). Here,
$\lambda \ll 1$). Here,  $Re_c = V_{wall}H/\nu$, where
$Re_c = V_{wall}H/\nu$, where  $H$ denotes the separation between the channel walls,
$H$ denotes the separation between the channel walls,  $V_\text {wall}$ denotes the speed of the moving wall, and
$V_\text {wall}$ denotes the speed of the moving wall, and  $\nu$ is the kinematic viscosity of the Newtonian suspending fluid. Also,
$\nu$ is the kinematic viscosity of the Newtonian suspending fluid. Also,  $\lambda = a/H$, where
$\lambda = a/H$, where  $a$ is the sphere radius, with
$a$ is the sphere radius, with  $Re_p=\lambda ^2 Re_c$. The channel centreline is found to be the only (stable) equilibrium below a critical
$Re_p=\lambda ^2 Re_c$. The channel centreline is found to be the only (stable) equilibrium below a critical  $Re_c$ (
$Re_c$ ( $\approx 148$), consistent with the predictions of earlier small-
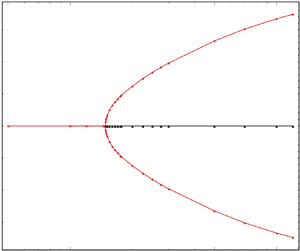
$\approx 148$), consistent with the predictions of earlier small- $Re_c$ analyses. A supercritical pitchfork bifurcation at the critical
$Re_c$ analyses. A supercritical pitchfork bifurcation at the critical  $Re_c$ creates a pair of stable off-centre equilibria, located symmetrically with respect to the centreline, with the original centreline equilibrium becoming unstable simultaneously. The new equilibria migrate wall-ward with increasing
$Re_c$ creates a pair of stable off-centre equilibria, located symmetrically with respect to the centreline, with the original centreline equilibrium becoming unstable simultaneously. The new equilibria migrate wall-ward with increasing  $Re_c$. In contrast to the inference based on recent computations, the aforementioned bifurcation occurs for arbitrarily small
$Re_c$. In contrast to the inference based on recent computations, the aforementioned bifurcation occurs for arbitrarily small  $Re_p$ provided that
$Re_p$ provided that  $\lambda$ is sufficiently small. An analogous bifurcation occurs in the two-dimensional scenario, that is, for a circular cylinder suspended freely in plane Couette flow, with the critical
$\lambda$ is sufficiently small. An analogous bifurcation occurs in the two-dimensional scenario, that is, for a circular cylinder suspended freely in plane Couette flow, with the critical  $Re_c$ being approximately
$Re_c$ being approximately  $110$.
$110$.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 4
- Cited by


