1. Introduction
Kolmogorov postulated in 1941 that the small scales of turbulent flows away from boundaries can be considered universal if the Reynolds number is sufficiently large (Kolmogorov Reference Kolmogorov1941). The small scales are then supposed to be in equilibrium, and the energy spectrum satisfies
where ![]() $\epsilon$ is the average energy dissipation rate. For this expression to hold, the wavenumber
$\epsilon$ is the average energy dissipation rate. For this expression to hold, the wavenumber ![]() $k$ should be sufficiently large compared to
$k$ should be sufficiently large compared to ![]() $L(\boldsymbol {x}, t)^{-1}$, the inverse of the length scale characterising the largest scales of the flow, and sufficiently small compared to the inverse of the Kolmogorov-scale
$L(\boldsymbol {x}, t)^{-1}$, the inverse of the length scale characterising the largest scales of the flow, and sufficiently small compared to the inverse of the Kolmogorov-scale ![]() $\eta (\boldsymbol {x}, t)^{-1}$ (with
$\eta (\boldsymbol {x}, t)^{-1}$ (with ![]() $\eta =\nu ^{3/4} \epsilon ^{-1/4}$), associated with the smallest scale of the flow.
$\eta =\nu ^{3/4} \epsilon ^{-1/4}$), associated with the smallest scale of the flow.
In (1.1), the time and space dependence of ![]() $E$ and
$E$ and ![]() $\epsilon$ need some particular attention. Theoretically, the most convenient flow type for investigating inertial range scaling is an infinitely large and statistically stationary flow without boundaries. Since all practical flows are limited in size and lifetime, the dissipation rate will be dependent, even on average, on either position
$\epsilon$ need some particular attention. Theoretically, the most convenient flow type for investigating inertial range scaling is an infinitely large and statistically stationary flow without boundaries. Since all practical flows are limited in size and lifetime, the dissipation rate will be dependent, even on average, on either position ![]() $\boldsymbol {x}$ or time
$\boldsymbol {x}$ or time ![]() $t$, or both. Therefore (1.1) will hold only locally in subdomains of space and time intervals large enough compared to the considered length and time scales.
$t$, or both. Therefore (1.1) will hold only locally in subdomains of space and time intervals large enough compared to the considered length and time scales.
Indeed, the assumptions allowing the simple prediction (1.1) are that the scales ![]() $k$ can be considered locally isotropic, stationary and homogeneous. The criterion
$k$ can be considered locally isotropic, stationary and homogeneous. The criterion ![]() $k \gg L^{-1}$ represents the implicit assumption that the influence of anisotropy, instationarity and inhomogeneity decreases as a function of scale. The present investigation aims to substantiate this assumption, particularly regarding the influence of inhomogeneity.
$k \gg L^{-1}$ represents the implicit assumption that the influence of anisotropy, instationarity and inhomogeneity decreases as a function of scale. The present investigation aims to substantiate this assumption, particularly regarding the influence of inhomogeneity.
As an illustration, let us discuss the influence of statistical instationarity on the behaviour of the small scales. This subject was addressed by Yoshizawa (Reference Yoshizawa1994), who proposed that the influence of instationarity at large wavenumbers can be described as a perturbation on the energy spectrum as
where the equilibrium part ![]() $E_0$ is given by (1.1), and the perturbation scales as
$E_0$ is given by (1.1), and the perturbation scales as
where the superscript ![]() $T$ denotes that we consider perturbations due to instationarity. Numerical evidence of this scaling was first obtained by Horiuti & Ozawa (Reference Horiuti and Ozawa2011) for the case of homogeneous shear flow, and by Horiuti & Tamaki (Reference Horiuti and Tamaki2013) for statistically isotropic turbulence in a periodic box. Further theoretical discussion and a more straightforward derivation of (1.3) can be found in Rubinstein & Clark (Reference Rubinstein and Clark2005), Woodruff & Rubinstein (Reference Woodruff and Rubinstein2006) and Bos & Rubinstein (Reference Bos and Rubinstein2017).
$T$ denotes that we consider perturbations due to instationarity. Numerical evidence of this scaling was first obtained by Horiuti & Ozawa (Reference Horiuti and Ozawa2011) for the case of homogeneous shear flow, and by Horiuti & Tamaki (Reference Horiuti and Tamaki2013) for statistically isotropic turbulence in a periodic box. Further theoretical discussion and a more straightforward derivation of (1.3) can be found in Rubinstein & Clark (Reference Rubinstein and Clark2005), Woodruff & Rubinstein (Reference Woodruff and Rubinstein2006) and Bos & Rubinstein (Reference Bos and Rubinstein2017).
A similar approach is applied in various other configurations where the influence of external effects on isotropic turbulence is modelled as a perturbation to the energy spectrum. The effect of a mean shear on isotropic turbulence was treated perturbatively by Ishihara, Yoshida & Kaneda (Reference Ishihara, Yoshida and Kaneda2002). Stratified turbulence was considered in Kaneda & Yoshida (Reference Kaneda and Yoshida2004), and the limit of weakly compressible turbulence by Bertoglio, Bataille & Marion (Reference Bertoglio, Bataille and Marion2001).
The effect of large-scale temporal fluctuations on the kinetic energy spectrum is thus proportional to ![]() $k^{-7/3}$, which decays more rapidly than the equilibrium spectrum (1.1) with the
$k^{-7/3}$, which decays more rapidly than the equilibrium spectrum (1.1) with the ![]() $k^{-5/3}$ scaling. In the remainder of this investigation, we will focus on the influence of inhomogeneity on the scaling of turbulent kinetic energy, which has received little attention. Using Karhunen–Loève eigenfunctions, it was illustrated that Kolmogorov's equilibrium spectrum can be observed in statistically inhomogeneous flows (Knight & Sirovich Reference Knight and Sirovich1990; Moser Reference Moser1994; Liao & Su Reference Liao and Su2015). By using the SO(3) symmetry group decomposition, Kurien et al. (Reference Kurien, L'vov, Procaccia and Sreenivasan2000) showed that structure functions contain a subdominant scaling component associated with inhomogeneity.
$k^{-5/3}$ scaling. In the remainder of this investigation, we will focus on the influence of inhomogeneity on the scaling of turbulent kinetic energy, which has received little attention. Using Karhunen–Loève eigenfunctions, it was illustrated that Kolmogorov's equilibrium spectrum can be observed in statistically inhomogeneous flows (Knight & Sirovich Reference Knight and Sirovich1990; Moser Reference Moser1994; Liao & Su Reference Liao and Su2015). By using the SO(3) symmetry group decomposition, Kurien et al. (Reference Kurien, L'vov, Procaccia and Sreenivasan2000) showed that structure functions contain a subdominant scaling component associated with inhomogeneity.
We further assess at which rate statistical homogeneity is recovered at small scales. To do that, in § 2 we derive an analytical prediction of the scaling of ![]() $E_1^X(k,\boldsymbol {x})$, where the superscript
$E_1^X(k,\boldsymbol {x})$, where the superscript ![]() $X$ denotes the perturbation due to inhomogeneity, in stationary inhomogeneous turbulence. This expression will be the inhomogeneous equivalent of (1.3). In § 3, we report the results of direct numerical simulations (DNS) of the three-dimensional Kolmogorov flow to assess the predictions. Section 4 concludes this investigation.
$X$ denotes the perturbation due to inhomogeneity, in stationary inhomogeneous turbulence. This expression will be the inhomogeneous equivalent of (1.3). In § 3, we report the results of direct numerical simulations (DNS) of the three-dimensional Kolmogorov flow to assess the predictions. Section 4 concludes this investigation.
2. Derivation of the spectral correction due to inhomogeneity
The main difficulty in the present investigation comes from the fact that we investigate a multi-scale description (the energy spectrum) in an inhomogeneous setting. To simplify as far as possible, we restrict ourselves to a fairly simple setting, where the (statistical) inhomogeneity is periodic in space, and the flow is stationary and far away from boundaries. Before addressing the inhomogeneous multi-scale description, we will first consider the pointwise energy balance of the flow.
2.1. Kinetic energy budget in inhomogeneous turbulence
We consider a statistically inhomogeneous flow kept in a statistically stationary state by a steady forcing ![]() $f(z)$. The forcing in the present paper consists of a unidirectional steady body force in the
$f(z)$. The forcing in the present paper consists of a unidirectional steady body force in the ![]() $x$-direction with a sinusoidal dependence in the
$x$-direction with a sinusoidal dependence in the ![]() $z$-direction. The Navier–Stokes equations for this specific system are
$z$-direction. The Navier–Stokes equations for this specific system are
where ![]() $\mathrm {D} / \mathrm {D}t$ is the material derivative,
$\mathrm {D} / \mathrm {D}t$ is the material derivative, ![]() $\mathcal {P}$ is the pressure (divided by density) ensuring incompressibility
$\mathcal {P}$ is the pressure (divided by density) ensuring incompressibility ![]() $\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {U}} = 0$, and
$\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\mathcal {U}} = 0$, and ![]() $\boldsymbol {e}_x$ denotes the unit vector in the
$\boldsymbol {e}_x$ denotes the unit vector in the ![]() $x$-direction.
$x$-direction.
The equations for the mean flow and the kinetic energy of the fluctuations can be derived by introducing the Reynolds decomposition ![]() $\boldsymbol {\mathcal {U}} = \langle \boldsymbol {\mathcal {U}}\rangle + \boldsymbol {u}$, where
$\boldsymbol {\mathcal {U}} = \langle \boldsymbol {\mathcal {U}}\rangle + \boldsymbol {u}$, where ![]() $\langle \boldsymbol {\mathcal {U}}\rangle$ is the ensemble-averaged velocity, and
$\langle \boldsymbol {\mathcal {U}}\rangle$ is the ensemble-averaged velocity, and ![]() $\boldsymbol {u} = (u, v, w)$ is the fluctuation. The specific forcing considered in the present investigation leads to a mean flow
$\boldsymbol {u} = (u, v, w)$ is the fluctuation. The specific forcing considered in the present investigation leads to a mean flow ![]() $\langle \boldsymbol {\mathcal {U}} (\boldsymbol {x}, t)\rangle = U(z)\,\boldsymbol {e}_x$. Then the kinetic energy corresponding to the mean flow can be written as
$\langle \boldsymbol {\mathcal {U}} (\boldsymbol {x}, t)\rangle = U(z)\,\boldsymbol {e}_x$. Then the kinetic energy corresponding to the mean flow can be written as
and the kinetic energy of the fluctuations is
The equation for the mean velocity ![]() $U(z)$ reduces to
$U(z)$ reduces to
The details are provided, for instance, in Bos (Reference Bos2020). The equation for the turbulent kinetic energy in a steady state is
where the production ![]() $p(z)$, dissipation
$p(z)$, dissipation ![]() $\epsilon (z)$ and diffusion
$\epsilon (z)$ and diffusion ![]() $d(z)$ terms are given by
$d(z)$ terms are given by
respectively. The first term, ![]() $p(z)$, represents the production of turbulent kinetic energy through the interaction of the turbulent fluctuations with the mean-velocity gradient
$p(z)$, represents the production of turbulent kinetic energy through the interaction of the turbulent fluctuations with the mean-velocity gradient ![]() $\partial U(z)/\partial z$. The viscous dissipation term
$\partial U(z)/\partial z$. The viscous dissipation term ![]() $\epsilon (z)$ involves the gradients of the fluctuating velocity.
$\epsilon (z)$ involves the gradients of the fluctuating velocity.
In statistically homogeneous flows, production and dissipation are the only terms appearing in the turbulent kinetic energy balance. In statistically inhomogeneous flows, we also have spatial diffusion of turbulent kinetic energy ![]() $d(z)$. The diffusion contains contributions associated with the turbulent fluctuations of the velocity and pressure (first two terms) and a contribution through viscous diffusion (the last term). This viscous part of the diffusion is generally negligible compared to the contribution of the other two terms and will be dropped in the following.
$d(z)$. The diffusion contains contributions associated with the turbulent fluctuations of the velocity and pressure (first two terms) and a contribution through viscous diffusion (the last term). This viscous part of the diffusion is generally negligible compared to the contribution of the other two terms and will be dropped in the following.
The main question in the present investigation is how such inhomogeneous redistribution processes ![]() $d(z)$ affect the scaling of the kinetic energy spectrum
$d(z)$ affect the scaling of the kinetic energy spectrum ![]() $E(k,\boldsymbol {x})$ in the inertial range of high-Reynolds-number turbulence.
$E(k,\boldsymbol {x})$ in the inertial range of high-Reynolds-number turbulence.
2.2. Fourier analysis of inhomogeneous turbulence
The use of energy spectra in general turbulent flows needs some justification. In principle, Fourier modes are associated with infinite or periodic domains. This property would exclude the use of spatial Fourier analysis of any realistic, non-periodic flow. However, a closer look at the length scales involved in turbulent flows permits invoking an assumption of scale separation, allowing us to get around this problem. Indeed, the theoretical basis for practical Fourier modelling of non-periodic turbulent flows can be found in various works (see Jeandel, Brison & Mathieu Reference Jeandel, Brison and Mathieu1978; Yoshizawa Reference Yoshizawa1984; Bertoglio & Jeandel Reference Bertoglio and Jeandel1987; Laporta & Bertoglio Reference Laporta and Bertoglio1995; Besnard et al. Reference Besnard, Harlow, Rauenzahn and Zemach1996). In practice, to develop a spectral description of inhomogeneous flows, one needs to introduce a length scale ![]() $L$ characterising the inhomogeneity of the flow geometry. Then one can consider Fourier spectra associated with scales
$L$ characterising the inhomogeneity of the flow geometry. Then one can consider Fourier spectra associated with scales ![]() $r\sim k^{-1}$ small compared to
$r\sim k^{-1}$ small compared to ![]() $L$.
$L$.
In the present investigation, we consider a spatially periodic flow without solid boundaries or obstacles to avoid most of these complications. Furthermore, to derive corrections due to statistical inhomogeneity, we consider statistically stationary turbulence with a single inhomogeneous direction ![]() $z$. An advantage of the present configuration, where only one inhomogeneous direction is present, is that we can compute energy spectra in planes perpendicular to the
$z$. An advantage of the present configuration, where only one inhomogeneous direction is present, is that we can compute energy spectra in planes perpendicular to the ![]() $z$-axis. We thus define
$z$-axis. We thus define
where ![]() $A(k_{\perp })$ denotes a wavenumber-shell of radius
$A(k_{\perp })$ denotes a wavenumber-shell of radius ![]() $k_\perp$ in the
$k_\perp$ in the ![]() $(k_x, k_y)$ plane. The velocity field in (2.9) is defined by the two-dimensional Fourier transform
$(k_x, k_y)$ plane. The velocity field in (2.9) is defined by the two-dimensional Fourier transform
The resulting energy spectrum ![]() $E(k_\perp, z)$ is a function of a perpendicular wavenumber
$E(k_\perp, z)$ is a function of a perpendicular wavenumber ![]() $k_\perp = \sqrt {k_x^2+k_y^2}$ and a vertical coordinate
$k_\perp = \sqrt {k_x^2+k_y^2}$ and a vertical coordinate ![]() $z$. We note that if isotropy is restored in small scales, then
$z$. We note that if isotropy is restored in small scales, then ![]() $E(k_\perp, z)$ is expected to scale like the three-dimensional spectrum
$E(k_\perp, z)$ is expected to scale like the three-dimensional spectrum ![]() $E(k, z)$ (see Appendix A for the definition). In the following subsections in § 2, we will keep the notation
$E(k, z)$ (see Appendix A for the definition). In the following subsections in § 2, we will keep the notation ![]() $E(k, z)$ for the sake of generality, but it should be kept in mind that the scaling of
$E(k, z)$ for the sake of generality, but it should be kept in mind that the scaling of ![]() $E(k, z)$ and
$E(k, z)$ and ![]() $E(k_\perp, z)$ should be equivalent in statistically isotropic flow at large
$E(k_\perp, z)$ should be equivalent in statistically isotropic flow at large ![]() $k$.
$k$.
2.3. Governing equation and modelling
The derivation in this subsection follows closely the rationale used to derive the instationary correction presented in Bos & Rubinstein (Reference Bos and Rubinstein2017). This same methodology is here applied to the evolution equation of the energy spectrum in inhomogeneous turbulence.
The kinetic energy spectrum is associated with the turbulent kinetic energy by the relation
The evolution equation for ![]() $E(k, z)$ is the multi-scale extension of (2.5). This equation reads, for the case of a unidirectional mean flow
$E(k, z)$ is the multi-scale extension of (2.5). This equation reads, for the case of a unidirectional mean flow ![]() $U(z)\,\boldsymbol {e}_x$ as in (2.1),
$U(z)\,\boldsymbol {e}_x$ as in (2.1),
 \begin{equation} \frac{\mathrm{D} E(k, z)}{\mathrm{D} t} =\underbrace{P(k, z)}_{production} -\underbrace{2\nu k^2\,E(k, z)}_{dissipation} + \underbrace{T(k, z)}_{transfer} + \underbrace{D(k, z)}_{diffusion}. \end{equation}
\begin{equation} \frac{\mathrm{D} E(k, z)}{\mathrm{D} t} =\underbrace{P(k, z)}_{production} -\underbrace{2\nu k^2\,E(k, z)}_{dissipation} + \underbrace{T(k, z)}_{transfer} + \underbrace{D(k, z)}_{diffusion}. \end{equation}For self-consistency, we discuss the derivation of this equation in Appendix A. Except for the viscous dissipation, all the terms in (2.12) are unclosed. In the following, we discuss the different physics and contributions to propose simple models for them.
Since the flow is statistically stationary and the mean flow is unidirectional, the material derivative on the left-hand side of (2.12) is zero. The first term on the right-hand side, ![]() $P(k, z)$, represents the terms directly proportional to the mean-velocity gradient. It contains two contributions: the production of turbulent kinetic energy and a linear transfer term (Cambon, Jeandel & Mathieu Reference Cambon, Jeandel and Mathieu1981; Briard et al. Reference Briard, Gréa, Mons, Cambon, Gomez and Sagaut2018). These terms are important mainly at large scales, and become zero at points in space where the velocity gradient vanishes. The order of magnitude of the production term can be estimated by (Tennekes & Lumley Reference Tennekes and Lumley1972),
$P(k, z)$, represents the terms directly proportional to the mean-velocity gradient. It contains two contributions: the production of turbulent kinetic energy and a linear transfer term (Cambon, Jeandel & Mathieu Reference Cambon, Jeandel and Mathieu1981; Briard et al. Reference Briard, Gréa, Mons, Cambon, Gomez and Sagaut2018). These terms are important mainly at large scales, and become zero at points in space where the velocity gradient vanishes. The order of magnitude of the production term can be estimated by (Tennekes & Lumley Reference Tennekes and Lumley1972),
with the time scale ![]() $\tau (k, z) \sim \epsilon (z)^{-1/3} k^{-2/3}$ in the inertial range. The integral of
$\tau (k, z) \sim \epsilon (z)^{-1/3} k^{-2/3}$ in the inertial range. The integral of ![]() $P(k, z)$ over wavenumbers yields
$P(k, z)$ over wavenumbers yields ![]() $p(z)$ in (2.5). Here,
$p(z)$ in (2.5). Here, ![]() $\epsilon (z)$ denotes the profile of the dissipation of kinetic energy through viscous stresses (see (2.7)) and is obtained by the integral of the second term on the right-hand side of (2.12). At large Reynolds numbers, this term is significant only at large wavenumbers. It is the term
$\epsilon (z)$ denotes the profile of the dissipation of kinetic energy through viscous stresses (see (2.7)) and is obtained by the integral of the second term on the right-hand side of (2.12). At large Reynolds numbers, this term is significant only at large wavenumbers. It is the term ![]() $P(k, z)$ that is responsible for energy transfer between the mean velocity field
$P(k, z)$ that is responsible for energy transfer between the mean velocity field ![]() $U(z)$ and the turbulent kinetic energy.
$U(z)$ and the turbulent kinetic energy.
The nonlinear transfer ![]() $T(k, z)$ represents the energy flux and is a redistributive term in scale space; thus its integral over all wavenumbers yields zero. The last term,
$T(k, z)$ represents the energy flux and is a redistributive term in scale space; thus its integral over all wavenumbers yields zero. The last term, ![]() $D(k, z)$, represents the diffusion, or transport, through turbulent fluctuations and viscous diffusion. Note that this term is zero in statistically homogeneous turbulence. The term
$D(k, z)$, represents the diffusion, or transport, through turbulent fluctuations and viscous diffusion. Note that this term is zero in statistically homogeneous turbulence. The term ![]() $D(k, z)$ is also a redistribution term like
$D(k, z)$ is also a redistribution term like ![]() $T(k, z)$, but in physical space. Its integral over wavenumbers corresponds to
$T(k, z)$, but in physical space. Its integral over wavenumbers corresponds to ![]() $d(z)$ in (2.5).
$d(z)$ in (2.5).
Both ![]() $T(k, z)$ and
$T(k, z)$ and ![]() $D(k, z)$ are functions of triple correlations between Fourier modes at different wavelengths. There is no exact expression of these quantities as a closed function of the kinetic energy spectrum
$D(k, z)$ are functions of triple correlations between Fourier modes at different wavelengths. There is no exact expression of these quantities as a closed function of the kinetic energy spectrum ![]() $E(k, z)$. At this moment, we will therefore introduce modelling assumptions. Sophisticated models exist for inhomogeneous spectral dynamics, based on the test field model (Kraichnan Reference Kraichnan1971) or the eddy-damped quasi-normal approximation (Laporta & Bertoglio Reference Laporta and Bertoglio1995; Parpais & Bertoglio Reference Parpais and Bertoglio1996). However, the resulting closures are quite complicated and do not allow a straightforward analytical perturbation treatment. Therefore, our approach uses simple models that reproduce their main physical features: the redistribution of energy in scale space for
$E(k, z)$. At this moment, we will therefore introduce modelling assumptions. Sophisticated models exist for inhomogeneous spectral dynamics, based on the test field model (Kraichnan Reference Kraichnan1971) or the eddy-damped quasi-normal approximation (Laporta & Bertoglio Reference Laporta and Bertoglio1995; Parpais & Bertoglio Reference Parpais and Bertoglio1996). However, the resulting closures are quite complicated and do not allow a straightforward analytical perturbation treatment. Therefore, our approach uses simple models that reproduce their main physical features: the redistribution of energy in scale space for ![]() $T(k, z)$, and in physical space for
$T(k, z)$, and in physical space for ![]() $D(k, z)$, respectively. We use diffusion approximations for both terms:
$D(k, z)$, respectively. We use diffusion approximations for both terms:
where ![]() $\varPi (k, z)$ and
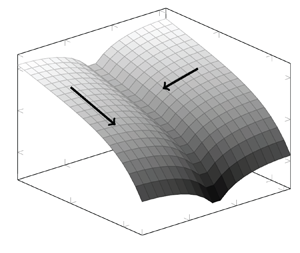
$\varPi (k, z)$ and ![]() $\varPhi (k, z)$ are turbulent fluxes in wavenumber and physical space, respectively. Figure 1 depicts schematically these two fluxes in
$\varPhi (k, z)$ are turbulent fluxes in wavenumber and physical space, respectively. Figure 1 depicts schematically these two fluxes in ![]() $(k,z)$ space. In the absence of inhomogeneity, the flux
$(k,z)$ space. In the absence of inhomogeneity, the flux ![]() $\varPhi (k, z)$ is zero. In the inhomogeneous case, the presence of this flux will affect the kinetic energy spectrum
$\varPhi (k, z)$ is zero. In the inhomogeneous case, the presence of this flux will affect the kinetic energy spectrum ![]() $E(k, z)$.
$E(k, z)$.

Figure 1. A schematic of the energy spectrum in ![]() $(k,z)$ coordinates. Two arrows denote the directions of energy fluxes in wavenumber and physical space, respectively.
$(k,z)$ coordinates. Two arrows denote the directions of energy fluxes in wavenumber and physical space, respectively.
We model both fluxes using a gradient-diffusion approximation
with ![]() $\rho (k, z) \sim k^{11/2}\,E(k, z)^{1/2}$ being a turbulent energy diffusion in Fourier space, and
$\rho (k, z) \sim k^{11/2}\,E(k, z)^{1/2}$ being a turbulent energy diffusion in Fourier space, and
where ![]() $\mu (z)$ is a turbulent diffusivity in real space (see (2.29)). We have effectively decoupled (and simplified) the transfer terms in scale and physical space. Indeed, both
$\mu (z)$ is a turbulent diffusivity in real space (see (2.29)). We have effectively decoupled (and simplified) the transfer terms in scale and physical space. Indeed, both ![]() $\varPhi (k, z)$ and
$\varPhi (k, z)$ and ![]() $\varPi (k, z)$ are determined by the same triple velocity and velocity–pressure correlations (see (A4)). Decomposing the physical space–scale space flux is a major assumption that seems necessary to obtain an analytically tractable model of energy transfer in inhomogeneous turbulence. The model (2.16) for
$\varPi (k, z)$ are determined by the same triple velocity and velocity–pressure correlations (see (A4)). Decomposing the physical space–scale space flux is a major assumption that seems necessary to obtain an analytically tractable model of energy transfer in inhomogeneous turbulence. The model (2.16) for ![]() $\varPi (k, z)$ is known as the Leith model (Leith Reference Leith1967; Rubinstein & Clark Reference Rubinstein and Clark2022). This model tends to homogenise the kinetic energy in spectral space towards equipartition among wave vectors, corresponding to an energy spectrum proportional to
$\varPi (k, z)$ is known as the Leith model (Leith Reference Leith1967; Rubinstein & Clark Reference Rubinstein and Clark2022). This model tends to homogenise the kinetic energy in spectral space towards equipartition among wave vectors, corresponding to an energy spectrum proportional to ![]() $k^2$. The gradient-diffusion model for the diffusion (2.17) tends to homogenise the energy distribution in physical space, and is used in Besnard et al. (Reference Besnard, Harlow, Rauenzahn and Zemach1996), Touil, Bertoglio & Shao (Reference Touil, Bertoglio and Shao2002) and Cadiou, Hanjalić & Stawiarski (Reference Cadiou, Hanjalić and Stawiarski2004), for instance.
$k^2$. The gradient-diffusion model for the diffusion (2.17) tends to homogenise the energy distribution in physical space, and is used in Besnard et al. (Reference Besnard, Harlow, Rauenzahn and Zemach1996), Touil, Bertoglio & Shao (Reference Touil, Bertoglio and Shao2002) and Cadiou, Hanjalić & Stawiarski (Reference Cadiou, Hanjalić and Stawiarski2004), for instance.
Eddy viscosity models are obviously simplified representations of the real transfer terms. For instance, see Pope (Reference Pope2000, § 10) for extensive discussion. However, we think that this kind of modelling is a useful first step before turning to more sophisticated modelling approaches.
2.4. Linear perturbation analysis and scaling predictions
Our goal is to derive a prediction for inertial range scaling at large Reynolds numbers in the limit of weak inhomogeneity, where the influence of inhomogeneity can be treated as a perturbation. In the following, the leading-order contributions and perturbations are indicated by subscripts ![]() $0$ and
$0$ and ![]() $1$, respectively. We define an inertial range
$1$, respectively. We define an inertial range ![]() $L^{-1} \ll k \ll \eta ^{-1}$, with the length
$L^{-1} \ll k \ll \eta ^{-1}$, with the length ![]() $L$ representing the typical length of the largest and energy-containing scales of the flow. Furthermore, in our description, it is associated with the longest wavelength in our flow domain and is chosen constant. We will define this length scale more precisely later, in § 2.5.
$L$ representing the typical length of the largest and energy-containing scales of the flow. Furthermore, in our description, it is associated with the longest wavelength in our flow domain and is chosen constant. We will define this length scale more precisely later, in § 2.5.
We now define the equilibrium about which we expand the equations. To do so, we consider the decomposition
with ![]() $|{E_1}| \ll |{E_0}|$. The other quantities, such as
$|{E_1}| \ll |{E_0}|$. The other quantities, such as ![]() $\varPi (k, z)$ and
$\varPi (k, z)$ and ![]() $\varPhi (k, z)$, are decomposed in the same manner. We recall here that in addition to these two contributions to the energy spectrum, the flow also contains the time-averaged velocity profile, which consists of a single wave vector in the
$\varPhi (k, z)$, are decomposed in the same manner. We recall here that in addition to these two contributions to the energy spectrum, the flow also contains the time-averaged velocity profile, which consists of a single wave vector in the ![]() $z$-direction in the present case (see (2.2)). This mean flow is not present in the inertial range, on which we will focus in the following. Therefore, in the remainder of this section, we can focus on the contributions
$z$-direction in the present case (see (2.2)). This mean flow is not present in the inertial range, on which we will focus in the following. Therefore, in the remainder of this section, we can focus on the contributions ![]() $E_0(k, z)$ and
$E_0(k, z)$ and ![]() $E_1(k, z)$.
$E_1(k, z)$.
For very high Reynolds numbers in the limit of vanishing inhomogeneity, we assume that the equilibrium contributions to the kinetic energy balance (2.12) do not depend on the inhomogeneous turbulent diffusion ![]() $D(k, z)$. By integrating the balance between the transfer and dissipation terms in (2.12) from
$D(k, z)$. By integrating the balance between the transfer and dissipation terms in (2.12) from ![]() $k$ to
$k$ to ![]() $\infty$, we find
$\infty$, we find
or, using (2.14) and the equilibrium/non-equilibrium decomposition,
Indeed, this corresponds to the equilibrium between the energy flux and the energy dissipation rate, essential to the inertial range description of Kolmogorov (Reference Kolmogorov1941). The constant flux solution of the Leith model is consistent with this framework and is given by
This expression defines our equilibrium solution. We now assess the influence of the inhomogeneity of ![]() $\epsilon (z)$ on this scaling as a perturbation.
$\epsilon (z)$ on this scaling as a perturbation.
In the following, we consider the terms in the balance equation (2.12) for the non-equilibrium contributions. The order of magnitude of the production term (2.13) and the diffusion-gradient modelling with the flux (2.17) lead us to deduce that ![]() $D(k, z)\gg P(k, z)$ at
$D(k, z)\gg P(k, z)$ at ![]() $k \gg L^{-1}$. Therefore, the first-order perturbation to the equilibrium scaling in the inertial range is due to the inhomogeneous diffusion
$k \gg L^{-1}$. Therefore, the first-order perturbation to the equilibrium scaling in the inertial range is due to the inhomogeneous diffusion ![]() $D(k, z)$. Then, in the inertial range, we have
$D(k, z)$. Then, in the inertial range, we have
and
since ![]() $\partial \varPi _0(k, z)/\partial k = 0$. Thus the first-order correction of the nonlinear transfer balances the zeroth-order contribution of the inhomogeneous diffusion. The first-order perturbation to the nonlinear flux
$\partial \varPi _0(k, z)/\partial k = 0$. Thus the first-order correction of the nonlinear transfer balances the zeroth-order contribution of the inhomogeneous diffusion. The first-order perturbation to the nonlinear flux ![]() $\varPi _1(k, z)$ is evaluated as (Rubinstein & Clark Reference Rubinstein and Clark2005)
$\varPi _1(k, z)$ is evaluated as (Rubinstein & Clark Reference Rubinstein and Clark2005)
where ![]() $\partial \varPi /\partial E|_{E_0}$ is the Fréchet derivative of the total flux
$\partial \varPi /\partial E|_{E_0}$ is the Fréchet derivative of the total flux ![]() $\varPi$ evaluated at
$\varPi$ evaluated at ![]() $E(k, z) = E_0(k, z)$. In the inertial range, assuming
$E(k, z) = E_0(k, z)$. In the inertial range, assuming ![]() $E_1$ to scale as a power law, this yields the scaling,
$E_1$ to scale as a power law, this yields the scaling,
Note that we obtain (2.25) not only for the Leith model, but also for most of the other classical closures, such as the Kovaznay and Heisenberg model (Rubinstein & Clark Reference Rubinstein and Clark2022). Integrating (2.23) from ![]() $k$ to
$k$ to ![]() $\infty$, we have
$\infty$, we have
By combining this with (2.17) and (2.25), we obtain
 \begin{equation} E_1 (k, z) \sim{-} \frac{E_0(k, z)}{\epsilon(z)}\,\frac{\partial}{\partial z} \left( \mu(z)\, \frac{\displaystyle\partial\int\nolimits_k^\infty E_0 (p, z) \,{\rm d}p}{\partial z} \right). \end{equation}
\begin{equation} E_1 (k, z) \sim{-} \frac{E_0(k, z)}{\epsilon(z)}\,\frac{\partial}{\partial z} \left( \mu(z)\, \frac{\displaystyle\partial\int\nolimits_k^\infty E_0 (p, z) \,{\rm d}p}{\partial z} \right). \end{equation}Substituting (2.21), the above expression gives
 \begin{equation} E_1(k, z) \sim{-}\mu(z)\,\epsilon(z)^{1/3}\,k^{{-}7/3} \left[ \frac23\,\frac{\epsilon_{zz}(z)}{\epsilon(z)} + \frac23\,\frac{\mu_z(z)}{\mu(z)}\,\frac{\epsilon_z(z)}{\epsilon(z)} - \frac29 \left(\frac{\epsilon_z(z)}{\epsilon(z)}\right)^2\right], \end{equation}
\begin{equation} E_1(k, z) \sim{-}\mu(z)\,\epsilon(z)^{1/3}\,k^{{-}7/3} \left[ \frac23\,\frac{\epsilon_{zz}(z)}{\epsilon(z)} + \frac23\,\frac{\mu_z(z)}{\mu(z)}\,\frac{\epsilon_z(z)}{\epsilon(z)} - \frac29 \left(\frac{\epsilon_z(z)}{\epsilon(z)}\right)^2\right], \end{equation}
where the subscripts denote derivatives with respect to ![]() $z$, for example,
$z$, for example, ![]() $\epsilon _{zz} = \partial ^2 \epsilon (z) / \partial z^2$. We will model the unknown eddy diffusivity in its simplest way,
$\epsilon _{zz} = \partial ^2 \epsilon (z) / \partial z^2$. We will model the unknown eddy diffusivity in its simplest way,
Doing so, we obtain
Note that although all the terms involving ![]() $\epsilon _z$ and
$\epsilon _z$ and ![]() $\mu _z$ vanish exactly for the current definition of
$\mu _z$ vanish exactly for the current definition of ![]() $\mu (z)$ in (2.29), this might not be the case for arbitrary choices of
$\mu (z)$ in (2.29), this might not be the case for arbitrary choices of ![]() $\mu (z)$. It is therefore possible that in more sophisticated descriptions of turbulent diffusion, terms involving first-order derivatives might appear. In our description this is, however, not the case at leading order.
$\mu (z)$. It is therefore possible that in more sophisticated descriptions of turbulent diffusion, terms involving first-order derivatives might appear. In our description this is, however, not the case at leading order.
Considering expressions (2.25) and (2.30), it is observed that the non-equilibrium contribution ![]() $\varPi _1(k,z)$ to the energy flux flux can change sign, according to the sign of
$\varPi _1(k,z)$ to the energy flux flux can change sign, according to the sign of ![]() $\epsilon _{zz}(z)$. This implies that this part of the flux can vary from large to small
$\epsilon _{zz}(z)$. This implies that this part of the flux can vary from large to small ![]() $k$ values in the inertial range. However, since
$k$ values in the inertial range. However, since ![]() $\varPi _1$ is small compared to
$\varPi _1$ is small compared to ![]() $\varPi _0$, the total flux in the inertial range, which is the sum of the two contributions, will be towards large
$\varPi _0$, the total flux in the inertial range, which is the sum of the two contributions, will be towards large ![]() $k$ as in the classical three-dimensional picture of an inertial range energy cascade.
$k$ as in the classical three-dimensional picture of an inertial range energy cascade.
2.5. Case of a sinusoidal dissipation profile
The comparison of (2.21) and (2.30) indicates that the inhomogeneous contribution (![]() $\propto k^{-7/3}$) is subdominant compared to the equilibrium energy spectrum (
$\propto k^{-7/3}$) is subdominant compared to the equilibrium energy spectrum (![]() $\propto k^{-5/3}$) at large wavenumbers. Furthermore, the expression is proportional to the second spatial derivative of the dissipation rate
$\propto k^{-5/3}$) at large wavenumbers. Furthermore, the expression is proportional to the second spatial derivative of the dissipation rate ![]() $\epsilon _{zz}(z)$ and can thus be both positive and negative. Let us illustrate the implication of this expression by considering a large-scale inhomogeneity characterised by a cosine function with a characteristic wavelength of order
$\epsilon _{zz}(z)$ and can thus be both positive and negative. Let us illustrate the implication of this expression by considering a large-scale inhomogeneity characterised by a cosine function with a characteristic wavelength of order ![]() $L$:
$L$:
with ![]() $\langle {\epsilon }\rangle \gg \tilde {\epsilon }$. We consider
$\langle {\epsilon }\rangle \gg \tilde {\epsilon }$. We consider ![]() $L$, first introduced in § 2.4, to be of the order of and proportional to the characteristic large-scale length of the flow. Substituting this expression for
$L$, first introduced in § 2.4, to be of the order of and proportional to the characteristic large-scale length of the flow. Substituting this expression for ![]() $\epsilon (z)$ in (2.30), we find
$\epsilon (z)$ in (2.30), we find
with
where the superscript ![]() $X$ indicates the perturbations due to inhomogeneity.
$X$ indicates the perturbations due to inhomogeneity.
Let us now assume that both the equilibrium spectrum ![]() $E_0(k, z)$ and
$E_0(k, z)$ and ![]() $E_1(k, z)$ extend from
$E_1(k, z)$ extend from ![]() $k=L^{-1}$ to
$k=L^{-1}$ to ![]() $\infty$. Integrating the spectra in this range, we find that
$\infty$. Integrating the spectra in this range, we find that
and
Comparing these last two expressions illustrates that the formal expansion parameter in our system is
The main analytical results of the present investigation, (2.33)–(2.35), are obtained by phenomenological modelling based on gradient-diffusion assumptions of nonlinear transfer in both physical and scale space. The models and their consequences are, at best, crude approximations of the intricate nonlinear interactions in the actual flow. Therefore, the resulting expressions need verification by experiments or DNS.
3. Assessment of the inhomogeneous scaling
3.1. Numerical set-up
In order to verify the theoretical predictions, in particular (2.33), we carry out DNS of three-dimensional Kolmogorov flow in a triple-periodic box. Such flow has the convenient properties of being statistically inhomogeneous in one direction and free of solid boundaries. Furthermore, its properties have been widely investigated numerically (Borue & Orszag Reference Borue and Orszag1996; Musacchio & Boffetta Reference Musacchio and Boffetta2014; Wu et al. Reference Wu, Schmitt, Calzavarini and Wang2021).
The dynamics of the Kolmogorov flow in the present investigation is governed by (2.1) with ![]() $f(z) = \sin (k_f z)$. The numerical domain is a cube of size
$f(z) = \sin (k_f z)$. The numerical domain is a cube of size ![]() $2{\rm \pi}$. These choices imply that the forcing wavelength is equal to the width of the cubic domain, and we set
$2{\rm \pi}$. These choices imply that the forcing wavelength is equal to the width of the cubic domain, and we set ![]() $k_f = L^{-1} = 1$. Simulations are carried out using a standard pseudo-spectral solver (Delache, Cambon & Godeferd Reference Delache, Cambon and Godeferd2014) with a third-order Adams–Bashforth time-integration scheme. The details of the simulations are reported in table 1. Since we focus on the effect of inhomogeneity, we attempt to obtain statistics in a steady state over a long-enough time interval to allow the effects of the temporal variations to become as small as possible (see the last column in table 1).
$k_f = L^{-1} = 1$. Simulations are carried out using a standard pseudo-spectral solver (Delache, Cambon & Godeferd Reference Delache, Cambon and Godeferd2014) with a third-order Adams–Bashforth time-integration scheme. The details of the simulations are reported in table 1. Since we focus on the effect of inhomogeneity, we attempt to obtain statistics in a steady state over a long-enough time interval to allow the effects of the temporal variations to become as small as possible (see the last column in table 1).
Table 1. DNS parameters and statistical quantities. The resolution ![]() $N$ and kinematic viscosity
$N$ and kinematic viscosity ![]() $\nu$ are the control parameters. The remaining statistical quantities are the fluctuating isotropic root mean square velocity
$\nu$ are the control parameters. The remaining statistical quantities are the fluctuating isotropic root mean square velocity ![]() $u' \equiv \sqrt {2K'/3}$, where the energy of the temporal fluctuating velocity is
$u' \equiv \sqrt {2K'/3}$, where the energy of the temporal fluctuating velocity is ![]() $K' \equiv \langle {u'_i u'_i}\rangle _{\boldsymbol {x}, t} / 2$ and
$K' \equiv \langle {u'_i u'_i}\rangle _{\boldsymbol {x}, t} / 2$ and ![]() $u'_i (\boldsymbol {x}, t) \equiv u_i (\boldsymbol {x}, t) - \langle {u_i}\rangle _t(\boldsymbol {x})$; the Taylor microscale
$u'_i (\boldsymbol {x}, t) \equiv u_i (\boldsymbol {x}, t) - \langle {u_i}\rangle _t(\boldsymbol {x})$; the Taylor microscale ![]() $\lambda \equiv u' \sqrt {15 \nu / \epsilon }$, where the energy dissipation rate is evaluated by
$\lambda \equiv u' \sqrt {15 \nu / \epsilon }$, where the energy dissipation rate is evaluated by ![]() $\epsilon = \nu \langle {\omega _i \omega _i}\rangle _{\boldsymbol {x}, t}$; the Taylor-length Reynolds number
$\epsilon = \nu \langle {\omega _i \omega _i}\rangle _{\boldsymbol {x}, t}$; the Taylor-length Reynolds number ![]() $Re_\lambda \equiv u' \lambda / \nu$; the integral time scale
$Re_\lambda \equiv u' \lambda / \nu$; the integral time scale ![]() $T \equiv L/u'$, with
$T \equiv L/u'$, with ![]() $L = k_f^{-1} = 1$; and the simulation time in the statistically steady state
$L = k_f^{-1} = 1$; and the simulation time in the statistically steady state ![]() $T_{total}$ as a function of
$T_{total}$ as a function of ![]() $T$.
$T$.

3.2. Visualisation and dissipation profile
In the following, we will discuss the simulation at the highest considered Reynolds number ![]() $Re_\lambda =184$. A flow visualisation is shown in figure 2(a) with the
$Re_\lambda =184$. A flow visualisation is shown in figure 2(a) with the ![]() $x$-component of the velocity field
$x$-component of the velocity field ![]() $\mathcal {U}_x (\boldsymbol {x}, t)$. The influence of the large-scale mean flow, proportional to the sinusoidal forcing along the
$\mathcal {U}_x (\boldsymbol {x}, t)$. The influence of the large-scale mean flow, proportional to the sinusoidal forcing along the ![]() $z$-axis, is distinguishable. Figure 2(b) shows the instantaneous profile of
$z$-axis, is distinguishable. Figure 2(b) shows the instantaneous profile of ![]() $\mathcal {U}_x (z, t) = \langle {\mathcal {U}_x (\boldsymbol {x}, t)}\rangle _{\perp }$. The single curve corresponds to the horizontal average of a snapshot, as shown in figure 2(a). Its time average
$\mathcal {U}_x (z, t) = \langle {\mathcal {U}_x (\boldsymbol {x}, t)}\rangle _{\perp }$. The single curve corresponds to the horizontal average of a snapshot, as shown in figure 2(a). Its time average ![]() $U(z) = \langle {\mathcal {U}_x (\boldsymbol {x}, t)}\rangle _{\perp, t}$ is also shown in figure 2(b) with a smooth sinusoidal profile.
$U(z) = \langle {\mathcal {U}_x (\boldsymbol {x}, t)}\rangle _{\perp, t}$ is also shown in figure 2(b) with a smooth sinusoidal profile.

Figure 2. (a) Instantaneous distributions of ![]() $\mathcal {U}_x(\boldsymbol {x}, t)$ at
$\mathcal {U}_x(\boldsymbol {x}, t)$ at ![]() $Re_\lambda =184$. Blue (red) corresponds to the negative (positive) value of
$Re_\lambda =184$. Blue (red) corresponds to the negative (positive) value of ![]() $\mathcal {U}_x$. (b) Instantaneous profiles of
$\mathcal {U}_x$. (b) Instantaneous profiles of ![]() $\mathcal {U}_x(z, t) = \langle {\mathcal {U}_x(\boldsymbol {x}, t)}\rangle _{\perp }$ in grey. Time-averaged profile
$\mathcal {U}_x(z, t) = \langle {\mathcal {U}_x(\boldsymbol {x}, t)}\rangle _{\perp }$ in grey. Time-averaged profile ![]() $U(z) = \langle {\mathcal {U}_x(\boldsymbol {x}, t)}\rangle _{\perp, t}$ is indicated by a thick line.
$U(z) = \langle {\mathcal {U}_x(\boldsymbol {x}, t)}\rangle _{\perp, t}$ is indicated by a thick line.
In figure 3(a), the instantaneous profile of the energy dissipation rate ![]() $\epsilon (z, t) = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\perp }$ is shown along with its time average
$\epsilon (z, t) = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\perp }$ is shown along with its time average ![]() $\epsilon (z) = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\perp, t}$. The instantaneous profile shows large fluctuations in comparison to the velocity profile (figure 2b). Its time average, in contrast, shows a smooth sinusoidal profile. This property allows us to use the approximations in § 2.5. As expected, the dissipation peaks at values where the mean velocity gradient is strongest (at
$\epsilon (z) = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\perp, t}$. The instantaneous profile shows large fluctuations in comparison to the velocity profile (figure 2b). Its time average, in contrast, shows a smooth sinusoidal profile. This property allows us to use the approximations in § 2.5. As expected, the dissipation peaks at values where the mean velocity gradient is strongest (at ![]() $z = 0$ and
$z = 0$ and ![]() $\pm {\rm \pi}$). For numerical convenience, we perform a sinusoidal fitting
$\pm {\rm \pi}$). For numerical convenience, we perform a sinusoidal fitting ![]() $\bar {\epsilon }(z)$ introduced in (2.31). This profile is also shown in figure 3(a).
$\bar {\epsilon }(z)$ introduced in (2.31). This profile is also shown in figure 3(a).

Figure 3. (a) Instantaneous profile of ![]() $\epsilon (z, t) = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\perp }$. The time-averaged profile
$\epsilon (z, t) = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\perp }$. The time-averaged profile ![]() $\epsilon (z) = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\perp, t}$ is also shown. The red dashed line denotes
$\epsilon (z) = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\perp, t}$ is also shown. The red dashed line denotes ![]() $\bar {\epsilon }(z)$, a sinusoidal fitting of
$\bar {\epsilon }(z)$, a sinusoidal fitting of ![]() $\epsilon (z)$ by (2.31). (b) Time-averaged profile of kinetic energy with fluctuating velocity
$\epsilon (z)$ by (2.31). (b) Time-averaged profile of kinetic energy with fluctuating velocity ![]() $K(z)$, and its equilibrium
$K(z)$, and its equilibrium ![]() $K_0(z)$ and non-equilibrium
$K_0(z)$ and non-equilibrium ![]() $K_1(z)$ contributions. See the main text and Appendix B for the definition.
$K_1(z)$ contributions. See the main text and Appendix B for the definition.
Figure 3(b) shows the kinetic energy profile of the fluctuating velocity field. The fluctuating energy profile is defined by ![]() $K(z, t) = \mathcal {K}(z, t) - K_U(z)$, where the total energy is
$K(z, t) = \mathcal {K}(z, t) - K_U(z)$, where the total energy is ![]() $\mathcal {K}(z, t) = \mathcal {U}_i (z, t)\,\mathcal {U}_i (z, t) / 2$ and the mean flow energy is
$\mathcal {K}(z, t) = \mathcal {U}_i (z, t)\,\mathcal {U}_i (z, t) / 2$ and the mean flow energy is ![]() $K_U(z) = U(z)^2 / 2$. We consider the decomposition (see (2.34)–(2.35) and Appendix B)
$K_U(z) = U(z)^2 / 2$. We consider the decomposition (see (2.34)–(2.35) and Appendix B)
In figure 3(b), we observe that the equilibrium ![]() $K_0(z) = \langle {K_0(z, t)}\rangle _t$ and the non-equilibrium
$K_0(z) = \langle {K_0(z, t)}\rangle _t$ and the non-equilibrium ![]() $K_1(z) = \langle {K_1(z, t)}\rangle _t$ profiles share the same phase, consistent with the prediction that the spectrum
$K_1(z) = \langle {K_1(z, t)}\rangle _t$ profiles share the same phase, consistent with the prediction that the spectrum ![]() $E_1(k, z)$ is proportional to
$E_1(k, z)$ is proportional to ![]() $-\partial ^2\epsilon (z)/\partial z^{2}$.
$-\partial ^2\epsilon (z)/\partial z^{2}$.
3.3. Equilibrium and non-equilibrium spectra
Figure 4 shows the isotropic energy spectrum ![]() $E(k, t)$ (see Appendix A for the definition) at three different Taylor-length Reynolds numbers. For simplicity, we denote its time average by
$E(k, t)$ (see Appendix A for the definition) at three different Taylor-length Reynolds numbers. For simplicity, we denote its time average by ![]() $E(k) = \langle {E(k, t)}\rangle _t$. Normalisation using
$E(k) = \langle {E(k, t)}\rangle _t$. Normalisation using ![]() $\nu$ and
$\nu$ and ![]() $\epsilon = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\boldsymbol {x}, t}$ allows an excellent collapse for large values of
$\epsilon = \langle {\epsilon (\boldsymbol {x}, t)}\rangle _{\boldsymbol {x}, t}$ allows an excellent collapse for large values of ![]() $k$.
$k$.

Figure 4. Time-averaged three-dimensional isotropic energy spectrum ![]() $E(k) = \langle {E(k, t)}\rangle _t$, normalised by Kolmogorov variables. Results are shown at
$E(k) = \langle {E(k, t)}\rangle _t$, normalised by Kolmogorov variables. Results are shown at ![]() $Re_\lambda =69.6$,
$Re_\lambda =69.6$, ![]() $113$ and
$113$ and ![]() $184$ (see table 1). The red dashed line denotes the
$184$ (see table 1). The red dashed line denotes the ![]() $k^{-5/3}$ scaling for reference.
$k^{-5/3}$ scaling for reference.
Next, we assess energy spectra in statistically homogeneous planes perpendicular to the ![]() $z$-axis, as defined in (2.9). In the following, we analyse the time-averaged inhomogeneous energy spectrum
$z$-axis, as defined in (2.9). In the following, we analyse the time-averaged inhomogeneous energy spectrum ![]() $E(k_\perp, z) = \langle {E(k_\perp, z, t)}\rangle _t$ in a statistically steady state (see table 1). Figure 5(a) shows
$E(k_\perp, z) = \langle {E(k_\perp, z, t)}\rangle _t$ in a statistically steady state (see table 1). Figure 5(a) shows ![]() $E(k_\perp, z)$ non-dimensionalised by
$E(k_\perp, z)$ non-dimensionalised by ![]() $\bar {\epsilon }(z)^{2/3}\,L^{2/3}$. The fluctuations at small scales are small, and variations are barely visible.
$\bar {\epsilon }(z)^{2/3}\,L^{2/3}$. The fluctuations at small scales are small, and variations are barely visible.

Figure 5. (a) Non-dimensionalised two-dimensional energy spectrum. Note that ![]() $E(k_\perp, z) = \langle {E(k_\perp, z, t)}\rangle _t$. Dark (light) colour represents the small (large) value of the
$E(k_\perp, z) = \langle {E(k_\perp, z, t)}\rangle _t$. Dark (light) colour represents the small (large) value of the ![]() $z$-coordinate. The thick black line denotes (3.3), the average over the
$z$-coordinate. The thick black line denotes (3.3), the average over the ![]() $z$-coordinate. (b) Time-averaged non-equilibrium energy spectrum with specific signs:
$z$-coordinate. (b) Time-averaged non-equilibrium energy spectrum with specific signs: ![]() $E_1^+ (k_\perp ) = \langle {E_1(k_\perp, z) > 0}\rangle _z$ and
$E_1^+ (k_\perp ) = \langle {E_1(k_\perp, z) > 0}\rangle _z$ and ![]() $E_1^- (k_\perp ) = \langle {E_1(k_\perp, t) < 0}\rangle _z$. Red dashed lines denote the
$E_1^- (k_\perp ) = \langle {E_1(k_\perp, t) < 0}\rangle _z$. Red dashed lines denote the ![]() $k_\perp ^{-7/3}$ slope.
$k_\perp ^{-7/3}$ slope.
Then we assume that the energy spectrum in the inertial range can be written, in a general form, as
where ![]() $f_L$ and
$f_L$ and ![]() $f_\eta$ determine the shapes at small and large
$f_\eta$ determine the shapes at small and large ![]() $k$, respectively. Therefore, there are two distinct choices to collapse the spectra. See Appendix B for the detail of the two normalisation procedures. In this study, we employ the large-scale normalisation and evaluate
$k$, respectively. Therefore, there are two distinct choices to collapse the spectra. See Appendix B for the detail of the two normalisation procedures. In this study, we employ the large-scale normalisation and evaluate
as shown in figure 5(a). Note that this expression is valid for ![]() $k_\perp \eta \ll 1$, where
$k_\perp \eta \ll 1$, where ![]() $f_\eta (k_\perp \eta )$ tends to a constant value. Then the equilibrium spectrum can be defined as
$f_\eta (k_\perp \eta )$ tends to a constant value. Then the equilibrium spectrum can be defined as
Now we can evaluate the non-equilibrium spectrum by ![]() $E_1(k_\perp, z) \equiv E(k_\perp, z) - E_0(k_\perp, z)$. Note that (i) this quantity is defined by the time-averaged spectra, and (ii) since this quantity can be regarded as a perturbation of
$E_1(k_\perp, z) \equiv E(k_\perp, z) - E_0(k_\perp, z)$. Note that (i) this quantity is defined by the time-averaged spectra, and (ii) since this quantity can be regarded as a perturbation of ![]() $E(k_\perp, z)$ around
$E(k_\perp, z)$ around ![]() $E_0(k_\perp, z)$, it can be both positive and negative. Figure 5(b) shows the
$E_0(k_\perp, z)$, it can be both positive and negative. Figure 5(b) shows the ![]() $z$-average of
$z$-average of ![]() $E(k_\perp, z)$ for specific signs.
$E(k_\perp, z)$ for specific signs.
Similar plots are shown in figure 10 of Horiuti & Ozawa (Reference Horiuti and Ozawa2011) and figure 2 of Horiuti & Tamaki (Reference Horiuti and Tamaki2013). The scaling is consistent with that derived in § 2.4, i.e.
Figure 6(a) compares ![]() $\langle {|{E_1(k_\perp, z)}|}\rangle _z$ for three different Reynolds numbers, as in figure 4. For smaller values of
$\langle {|{E_1(k_\perp, z)}|}\rangle _z$ for three different Reynolds numbers, as in figure 4. For smaller values of ![]() $Re_\lambda$, the spectrum exhibits scaling steeper than
$Re_\lambda$, the spectrum exhibits scaling steeper than ![]() $k_\perp ^{-7/3}$. At larger
$k_\perp ^{-7/3}$. At larger ![]() $Re_\lambda$, the slope approaches the
$Re_\lambda$, the slope approaches the ![]() $k_\perp ^{-7/3}$ scaling. At the same time, the spectrum in the higher
$k_\perp ^{-7/3}$ scaling. At the same time, the spectrum in the higher ![]() $k_\perp$ range exhibits a bump associated with scaling shallower than
$k_\perp$ range exhibits a bump associated with scaling shallower than ![]() $k_\perp ^{-7/3}$.
$k_\perp ^{-7/3}$.

Figure 6. (a) Absolute value of the time-averaged non-equilibrium energy spectrum ![]() $|{E_1(k_\perp, z)}| = |{\langle {E_1(k_\perp, z, t)}\rangle _t}|$ for three values of the Taylor-length Reynolds numbers. The red dashed line represents the
$|{E_1(k_\perp, z)}| = |{\langle {E_1(k_\perp, z, t)}\rangle _t}|$ for three values of the Taylor-length Reynolds numbers. The red dashed line represents the ![]() $k_\perp ^{-7/3}$ scaling. (b) Compensated spectrum of (a). The red dashed line denotes the compensated
$k_\perp ^{-7/3}$ scaling. (b) Compensated spectrum of (a). The red dashed line denotes the compensated ![]() $k_\perp ^{-7/3}$ scaling.
$k_\perp ^{-7/3}$ scaling.
We plot the compensated spectra in figure 6(b). Although the scaling range extends for less than a decade, the emergence of the ![]() $k_\perp ^{-7/3}$ scaling range is well captured using this normalisation. In Appendix B, we confirm that the bump in the compensated spectra is due to our choice of the non-dimensional function (3.2).
$k_\perp ^{-7/3}$ scaling range is well captured using this normalisation. In Appendix B, we confirm that the bump in the compensated spectra is due to our choice of the non-dimensional function (3.2).
4. Conclusion and discussion
The numerical simulations in the previous section support our prediction,
of the energy spectrum for turbulence with inhomogeneity in the ![]() $z$-direction. This scaling quantifies the influence of spatial inhomogeneity in wavenumber space. In particular, the special case where the dissipation fluctuates as a sinusoidal function around a mean value, discussed in § 2.5, gives us a useful estimate of the influence of inhomogeneity (see (2.32)–(2.33)). Indeed, introducing an average dissipation
$z$-direction. This scaling quantifies the influence of spatial inhomogeneity in wavenumber space. In particular, the special case where the dissipation fluctuates as a sinusoidal function around a mean value, discussed in § 2.5, gives us a useful estimate of the influence of inhomogeneity (see (2.32)–(2.33)). Indeed, introducing an average dissipation ![]() $\langle {\epsilon }\rangle$ and smooth spatial fluctuations
$\langle {\epsilon }\rangle$ and smooth spatial fluctuations ![]() $\tilde {\epsilon }$ around
$\tilde {\epsilon }$ around ![]() $\langle {\epsilon }\rangle$, so that
$\langle {\epsilon }\rangle$, so that ![]() $\epsilon _{zz}/\tilde {\epsilon }\sim L^{-2}$, we obtain
$\epsilon _{zz}/\tilde {\epsilon }\sim L^{-2}$, we obtain
This expression shows that the influence of large-scale inhomogeneity is negligible for
 \begin{equation} k \gg L^{{-}1}\left(\frac{\tilde{\epsilon}}{\langle{\epsilon}\rangle}\right)^{3/2}. \end{equation}
\begin{equation} k \gg L^{{-}1}\left(\frac{\tilde{\epsilon}}{\langle{\epsilon}\rangle}\right)^{3/2}. \end{equation}Therefore, if this requirement is fulfilled in a statistically stationary flow, far enough away from walls, then Kolmogorov's equilibrium spectrum is expected to be dominant compared to the contributions associated with spatial inhomogeneity.
Funding
We dedicate this work to J.-P. Bertoglio, on the occasion of his retirement. All DNS were carried out using the facilities of the PMCS2I (École Centrale de Lyon). R.A. is supported by the Takenaka Scholarship Foundation.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Governing equation of the inhomogeneous energy spectrum
In this appendix, we define the spectrum and the governing equations for the energy spectrum tensor in inhomogeneous flow (see (2.12)). The generalised spectrum ![]() $E(k, \boldsymbol {x}) = E_{ii} (k, \boldsymbol {x})$ is defined by
$E(k, \boldsymbol {x}) = E_{ii} (k, \boldsymbol {x})$ is defined by
where ![]() $\int {\rm d}{\varOmega _k}$ denotes the integral over spherical shells of radius
$\int {\rm d}{\varOmega _k}$ denotes the integral over spherical shells of radius ![]() $k$. The brackets in this appendix denote the ensemble average. For statistically homogeneous turbulence, this definition is equivalent to the expression
$k$. The brackets in this appendix denote the ensemble average. For statistically homogeneous turbulence, this definition is equivalent to the expression
The evolution equation for ![]() $E_{ij} (k, \boldsymbol {x}, t)$ formally reads
$E_{ij} (k, \boldsymbol {x}, t)$ formally reads
For the tensor on the right-hand side, we have
 \begin{align} \varPsi_{ij}
(\boldsymbol{x}_1, \boldsymbol{x}_2) &= \nu
\left(\nabla^2_1 + \nabla^2_2\right) R_{ij}
(\boldsymbol{x}_1, \boldsymbol{x}_2) \nonumber\\ &\quad -
\left[\frac{\partial}{\partial x_{1n}} U_n
(\boldsymbol{x}_1)\,R_{ij}
(\boldsymbol{x}_1,\boldsymbol{x}_2) +
\frac{\partial}{\partial x_{2n}} U_n
(\boldsymbol{x}_2)\,R_{ij}
(\boldsymbol{x}_1,\boldsymbol{x}_2)\right.\nonumber\\
&\quad + \left. \frac{\partial}{\partial x_{1n}} U_i
(\boldsymbol{x}_1)\,R_{nj}
(\boldsymbol{x}_1,\boldsymbol{x}_2) +
\frac{\partial}{\partial x_{2n}} U_j
(\boldsymbol{x}_2)\,R_{ni}
(\boldsymbol{x}_1,\boldsymbol{x}_2)\right. \nonumber\\ &\quad + \left.
\frac{\partial}{\partial x_{1i}} \langle{
\mathcal{P}(\boldsymbol{x}_1)\,u_j(\boldsymbol{x}_2)
}\rangle + \frac{\partial}{\partial x_{2j}} \langle{
\mathcal{P}(\boldsymbol{x}_2)\,u_i(\boldsymbol{x}_1)
}\rangle \right.\nonumber\\ &\quad + \left.
\frac{\partial}{\partial x_{1n}}
\langle{u_i(\boldsymbol{x}_1)\,u_n(\boldsymbol{x}_1)\,u_j(\boldsymbol{x}_2)
}\rangle + \frac{\partial}{\partial x_{2n}} \langle{
u_j(\boldsymbol{x}_2)\,u_n(\boldsymbol{x}_2)\,u_i(\boldsymbol{x}_1)
}\rangle\right].
\end{align}
\begin{align} \varPsi_{ij}
(\boldsymbol{x}_1, \boldsymbol{x}_2) &= \nu
\left(\nabla^2_1 + \nabla^2_2\right) R_{ij}
(\boldsymbol{x}_1, \boldsymbol{x}_2) \nonumber\\ &\quad -
\left[\frac{\partial}{\partial x_{1n}} U_n
(\boldsymbol{x}_1)\,R_{ij}
(\boldsymbol{x}_1,\boldsymbol{x}_2) +
\frac{\partial}{\partial x_{2n}} U_n
(\boldsymbol{x}_2)\,R_{ij}
(\boldsymbol{x}_1,\boldsymbol{x}_2)\right.\nonumber\\
&\quad + \left. \frac{\partial}{\partial x_{1n}} U_i
(\boldsymbol{x}_1)\,R_{nj}
(\boldsymbol{x}_1,\boldsymbol{x}_2) +
\frac{\partial}{\partial x_{2n}} U_j
(\boldsymbol{x}_2)\,R_{ni}
(\boldsymbol{x}_1,\boldsymbol{x}_2)\right. \nonumber\\ &\quad + \left.
\frac{\partial}{\partial x_{1i}} \langle{
\mathcal{P}(\boldsymbol{x}_1)\,u_j(\boldsymbol{x}_2)
}\rangle + \frac{\partial}{\partial x_{2j}} \langle{
\mathcal{P}(\boldsymbol{x}_2)\,u_i(\boldsymbol{x}_1)
}\rangle \right.\nonumber\\ &\quad + \left.
\frac{\partial}{\partial x_{1n}}
\langle{u_i(\boldsymbol{x}_1)\,u_n(\boldsymbol{x}_1)\,u_j(\boldsymbol{x}_2)
}\rangle + \frac{\partial}{\partial x_{2n}} \langle{
u_j(\boldsymbol{x}_2)\,u_n(\boldsymbol{x}_2)\,u_i(\boldsymbol{x}_1)
}\rangle\right].
\end{align}
In this expression and the following, the argument ![]() $t$ for time is omitted for visibility. The two-point velocity tensor is defined by
$t$ for time is omitted for visibility. The two-point velocity tensor is defined by
and (A4) is completed by incompressibility conditions for the mean field and the fluctuations.
Both inhomogeneous turbulence diffusion and spectral transfer are associated with the last two lines of expression (A4). An assumption of weak inhomogeneity must be invoked to dissociate them to obtain a closed expression. Even retaining only the leading-order terms in an expansion about inhomogeneity, the resulting equations become quite cumbersome (see Laporta Reference Laporta1995; Besnard et al. Reference Besnard, Harlow, Rauenzahn and Zemach1996).
Subsequently, the different terms in (A4) need to be modelled to close the triple correlations. We will not proceed in this direction, and will model them directly by their physical effects. See (2.13)– (2.16).
Appendix B. Normalisation to extract the non-equilibrium spectrum and kinetic energy profile
In this appendix, we investigate the different normalisation procedures mentioned in § 3.3. We state that the energy spectrum is decomposed into equilibrium (labelled by the subscript ![]() $0$) and non-equilibrium (labelled by the subscript
$0$) and non-equilibrium (labelled by the subscript ![]() $1$) contributions as
$1$) contributions as
We further assume that the non-equilibrium contributions are zero-mean:
We have therefore
In order to compute the non-equilibrium contributions ![]() $E_1(k, z) = E(k, z) - E_0(k, z)$, we need to know the
$E_1(k, z) = E(k, z) - E_0(k, z)$, we need to know the ![]() $z$-dependence of
$z$-dependence of ![]() $E_0(k, z)$. For this purpose, we use self-similarity assumptions and Kolmogorov's equilibrium hypothesis.
$E_0(k, z)$. For this purpose, we use self-similarity assumptions and Kolmogorov's equilibrium hypothesis.
Scaling ranges in turbulence spectra appear when scale separation is attained, i.e. at sufficiently high Reynolds numbers. In general, one can write the energy spectrum to scale as (see (3.2))
at high Reynolds numbers. We have two non-dimensional functions in (B4): ![]() $f_L$ determines the shape of the spectrum for small
$f_L$ determines the shape of the spectrum for small ![]() $k$ (large scale), and
$k$ (large scale), and ![]() $f_\eta$ determines it for large
$f_\eta$ determines it for large ![]() $k$ (small scale). These functions satisfy the framework of Kolmogorov (Reference Kolmogorov1941):
$k$ (small scale). These functions satisfy the framework of Kolmogorov (Reference Kolmogorov1941):
Therefore, we retrieve (1.1) for scales ![]() $L^{-1} \ll k \ll \eta ^{-1}$ in the limit
$L^{-1} \ll k \ll \eta ^{-1}$ in the limit ![]() $L/\eta \rightarrow \infty$. Multiplying both sides of (B4) by
$L/\eta \rightarrow \infty$. Multiplying both sides of (B4) by ![]() $\eta ^{-5/3}$, and dividing by
$\eta ^{-5/3}$, and dividing by ![]() $\epsilon ^{2/3}$, we obtain
$\epsilon ^{2/3}$, we obtain
with
Since ![]() $F(kL)$ tends to unity for
$F(kL)$ tends to unity for ![]() $k \gg 1/L$, the equilibrium spectra
$k \gg 1/L$, the equilibrium spectra ![]() $E_0(k, z)$ should collapse when normalised by (B6) for any
$E_0(k, z)$ should collapse when normalised by (B6) for any ![]() $z$, for large
$z$, for large ![]() $kL$.
$kL$.
Similarly, if the large scales are characterised by a length scale ![]() $L$, then we can propose an alternative normalisation for (B6):
$L$, then we can propose an alternative normalisation for (B6):
with
It should scale as purely a function of ![]() $kL$ for
$kL$ for ![]() $k\eta \ll 1$.
$k\eta \ll 1$.
There are therefore two normalisation possibilities. One focuses on the high wavenumber limit of the inertial range close to the dissipation range (B6)–(B7), and the other one on the low-![]() $k$ range close to the energy range (B8)–(B9). In the limit of infinite Reynolds number, we should find them to be equivalent in the inertial range, since
$k$ range close to the energy range (B8)–(B9). In the limit of infinite Reynolds number, we should find them to be equivalent in the inertial range, since
Figure 7 plots the absolute value of the non-equilibrium energy spectrum ![]() $E_1(k_\perp, z)$ for these two normalisations. It is observed that using
$E_1(k_\perp, z)$ for these two normalisations. It is observed that using ![]() $F[kL]$, we reveal a larger inertial range. We will therefore use this normalisation in the present investigation.
$F[kL]$, we reveal a larger inertial range. We will therefore use this normalisation in the present investigation.

Figure 7. Absolute value of the time-averaged non-equilibrium energy spectrum ![]() $|{E_1(k_\perp, z)}| = |{\langle {E_1(k_\perp, z, t)}\rangle _t}|$ for the highest Reynolds number dataset. Different non-dimensionalised functions are employed to compute the non-equilibrium spectrum: (a) with (B7), and (b) with (B9). The black solid and red dashed lines denote the
$|{E_1(k_\perp, z)}| = |{\langle {E_1(k_\perp, z, t)}\rangle _t}|$ for the highest Reynolds number dataset. Different non-dimensionalised functions are employed to compute the non-equilibrium spectrum: (a) with (B7), and (b) with (B9). The black solid and red dashed lines denote the ![]() $z$-average and
$z$-average and ![]() $k_\perp ^{-7/3}$ scaling, respectively.
$k_\perp ^{-7/3}$ scaling, respectively.
We have checked the data, and we verified that the spectra ![]() $E_1(k_\perp,z)$ are for a given
$E_1(k_\perp,z)$ are for a given ![]() $z$ of a single sign, with a very occasional sign change when the statistics are determined over a too short time interval. Perturbation spectra are, as predicted, proportional to
$z$ of a single sign, with a very occasional sign change when the statistics are determined over a too short time interval. Perturbation spectra are, as predicted, proportional to ![]() $-\epsilon _{zz}(z)$, as is also the case for
$-\epsilon _{zz}(z)$, as is also the case for ![]() $K_1(z)$, as can be seen by comparing figures 3(a) and 3(b). The procedure to determine
$K_1(z)$, as can be seen by comparing figures 3(a) and 3(b). The procedure to determine ![]() $K_1(z)$ is now outlined.
$K_1(z)$ is now outlined.
Since the kinetic energy is determined dominantly by large scales, (B8) allows us to determine the equilibrium kinetic energy profile:
with ![]() $C_L = \int F_L [x] \,{\rm d}\kern0.06em x$. Then we define the decomposition
$C_L = \int F_L [x] \,{\rm d}\kern0.06em x$. Then we define the decomposition
where ![]() $\langle {K_0 (z)}\rangle _z = \langle {K(z)}\rangle _z$ follows from the assumption that
$\langle {K_0 (z)}\rangle _z = \langle {K(z)}\rangle _z$ follows from the assumption that ![]() $\langle {K_1(z)}\rangle _z = 0$. By employing the decomposition for the energy dissipation rate profile
$\langle {K_1(z)}\rangle _z = 0$. By employing the decomposition for the energy dissipation rate profile
it follows from (B11) that
 \begin{equation} \frac{\tilde{K}_0(z)}{\langle{K_0(z)}\rangle_z} = \frac{\widetilde{\epsilon(z)^{2/3}}}{\langle{\epsilon(z)^{2/3}}\rangle_z}, \end{equation}
\begin{equation} \frac{\tilde{K}_0(z)}{\langle{K_0(z)}\rangle_z} = \frac{\widetilde{\epsilon(z)^{2/3}}}{\langle{\epsilon(z)^{2/3}}\rangle_z}, \end{equation}and by (B12),
 \begin{equation} K_0(z) = \left(1 + \frac{\widetilde{\epsilon(z)^{2/3}}}{\langle{\epsilon(z)^{2/3}}\rangle_z}\right) \langle{K(z)}\rangle_z. \end{equation}
\begin{equation} K_0(z) = \left(1 + \frac{\widetilde{\epsilon(z)^{2/3}}}{\langle{\epsilon(z)^{2/3}}\rangle_z}\right) \langle{K(z)}\rangle_z. \end{equation}
Since all the terms on the right-hand side are known, one can evaluate the non-equilibrium kinetic energy profile ![]() $K_1(z) = K(z) - K_0(z)$ (see (3.1)).
$K_1(z) = K(z) - K_0(z)$ (see (3.1)).