Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-04T08:30:37.027Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial solution for high-pressure-difference pulse-decay measurement through microporous media

Published online by Cambridge University Press:  21 September 2023

Zhiguo Tian ,
Duzhou Zhang ,
Yue Wang ,
Gang Zhou ,
Shaohua Zhang  and
Moran Wang Open the ORCID record for Moran Wang [Opens in a new window]
Zhiguo Tian
Affiliation:
Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Duzhou Zhang
Affiliation:
Beijing Institute of Control Engineering, Beijing, PR China
Yue Wang
Affiliation:
Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Gang Zhou
Affiliation:
Beijing Institute of Control Engineering, Beijing, PR China
Shaohua Zhang
Affiliation:
Beijing Institute of Control Engineering, Beijing, PR China
Moran Wang*
Affiliation:
Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
*
†Email address for correspondence: moralwang@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

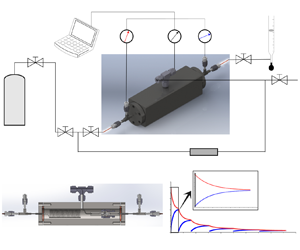
We present a theoretical asymptotic solution for high-speed transient flow through microporous media in this work by addressing the inertia effect in the high-pressure-difference pulse-decay process. The capillaric model is adopted, in which a bundle of straight circular tubes with a high length–radius ratio is used to represent the internal flow paths of microporous media so that the flow is described by a simplified incompressible Navier–Stokes equation based on the mean density, capturing the major characteristics of mass flow rate. By order-of-magnitude analysis and asymptotic perturbation, the inertial solution with its dimensionless criterion for the high-pressure-difference pulse-decay process is derived. To be compared with experimental data, the theoretical solution involves all three related effects, including the inertia effect, the slippage effect and the compressibility effect. A self-built experimental platform is therefore established to measure the permeability of microporous media by both pulse-decay and steady-state methods to validate the theoretical solution. The results indicate that the relative difference between two methods is less than 30 % even for permeability at as low as $48.2$ nD $(10^{-21}\,{\rm m}^2)$, and the present theoretical solution can accurately capture the inertia effect in the high-pressure-difference pulse-decay process, which significantly accelerates the measurements for ultra-low-permeability samples.

JFM classification

Low-Reynolds-number flows: Porous media
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 971 , 25 September 2023 , R1
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, P.M. & Brenner, H. 1988 Multiphase flow in porous media. Annu. Rev. Fluid Mech. 20, 35–59.CrossRefGoogle Scholar
Andrade, J.S., Costa, U.M.S., Almeida, M.P., Makse, H.A. & Stanley, H.E. 1999 Inertial effects on fluid flow through disordered porous media. Phys. Rev. Lett. 82, 5249.CrossRefGoogle Scholar
Arkilic, E.B., Schmidt, M.A. & Breuer, K.S. 1997 Gaseous slip flow in long microchannels. J. Microelectromech. Syst. 6, 167–178.CrossRefGoogle Scholar
Brace, W.F., Walsh, J.B. & Frangos, W.T. 1968 Permeability of granite under high pressure. J. Geophys. Res. 73, 2225–2236.CrossRefGoogle Scholar
Cai, C., Sun, Q. & Boyd, I.D. 2007 Gas flows in microchannels and microtubes. J. Fluid Mech. 589, 305–314.CrossRefGoogle Scholar
Cui, X., Bustin, A. & Bustin, R.M. 2009 Measurements of gas permeability and diffusivity of tight reservoir rocks: different approaches and their applications. Geofluids 9, 208–223.CrossRefGoogle Scholar
Darabi, H., Ettehad, A., Javadpour, F. & Sepehrnoori, K. 2012 Gas flow in ultra-tight shale strata. J. Fluid Mech. 710, 641–658.CrossRefGoogle Scholar
Gensterblum, Y., Ghanizadeh, A., Cuss, R.J., Amann-hildenbrand, A., Krooss, B.M., Clarkson, C.R., Harrington, J.F. & Zoback, M.D. 2015 Gas transport and storage capacity in shale gas reservoirs–a review. Part A. Transport processes. J. Unconv. Oil Gas Resour. 12, 87–122.CrossRefGoogle Scholar
Hill, R.J., Koch, D.L. & Ladd, A.J. 2001 Moderate-Reynolds-number flows in ordered and random arrays of spheres. J. Fluid Mech. 448, 243–278.CrossRefGoogle Scholar
Hsieh, P.A., Tracy, J.V., Neuzil, C.E., Bredehoeft, J.D. & Silliman, S.E. 1981 A transient laboratory method for determining the hydraulic properties of ‘tight’ rocks–I. Theory. Intl J. Rock Mech. Min. Sci. Geomech. Abstr. 18, 245–252.CrossRefGoogle Scholar
Huppert, H.E. & Neufeld, J.A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46, 255–272.CrossRefGoogle Scholar
Jones, C. 1997 A technique for faster pulse-decay permeability measurements in tight rocks. SPE Formation Eval. 12, 19–26.CrossRefGoogle Scholar
Jones, S.C. 1972 A rapid accurate unsteady-state Klinkenberg permeameter. Soc. Petrol. Engng J. 12, 383–397.CrossRefGoogle Scholar
Klinkenberg, L.J. 1941 The permeability of porous media to liquids and gases. Drill. Prod. Practice 2, 200–213.Google Scholar
Kranz, R.L., Saltzman, J.S. & Blacic, J.D. 1990 Hydraulic diffusivity measurements on laboratory rock samples using an oscillating pore pressure method. Intl J. Rock Mech. Min. Sci. Geomech. Abstr. 27, 345–352.CrossRefGoogle Scholar
Lionel Pullum, D.V.B. & Sofra, F. 2018 Hydraulic mineral waste transport and storage. Annu. Rev. Fluid Mech. 50, 157–185.CrossRefGoogle Scholar
Mahabadi, N., Dai, S., Seol, Y. & Jang, J. 2019 Impact of hydrate saturation on water permeability in hydrate-bearing sediments. J. Petrol. Sci. Engng 174, 696–703.CrossRefGoogle Scholar
Mei, C.C. & Auriault, J.L. 1991 The effect of weak inertia on flow through a porous medium. J. Fluid Mech. 222, 647–663.CrossRefGoogle Scholar
Morrow, C. & Lockner, D. 1994 Permeability differences between surface-derived and deep drillhole core samples. Geophys. Res. Lett. 21, 2151–2154.CrossRefGoogle Scholar
Muskat, M. 1937 The Flow of Homogeneous Fluids through Porous Media, pp. 76–79. McGraw-Hill.Google Scholar
Neuzil, C.E. 2019 Permeability of clays and shales. Annu. Rev. Earth Planet. Sci. 47, 247–273.CrossRefGoogle Scholar
Polyanin, A.D. & Nazaikinskii, V.E. 2015 Handbook of Linear Partial Differential Equations for Engineers and Scientists, pp. 261–288. CRC Press.CrossRefGoogle Scholar
Sander, R., Pan, Z. & Connell, L.D. 2017 Laboratory measurement of low permeability unconventional gas reservoir rocks: a review of experimental methods. J. Nat. Gas Sci. Engng 37, 248–279.CrossRefGoogle Scholar
Veltzke, T. & Thöming, J. 2012 An analytically predictive model for moderately rarefied gas flow. J. Fluid Mech. 698, 406–422.CrossRefGoogle Scholar
Wang, K., Du, F. & Wang, G. 2017 Investigation of gas pressure and temperature effects on the permeability and steady-state time of Chinese anthracite coal: an experimental study. J. Nat. Gas Sci. Engng 40, 179–188.CrossRefGoogle Scholar
Wang, Y., Nolte, S., Gaus, G., Tian, Z., Hildenbrand, A.A., Krooss, B. & Wang, M. 2021 An early-time solution of pulse-decay method for permeability measurement of tight rocks. J. Geophys. Res. 126, e2021JB022422.CrossRefGoogle Scholar
Wang, Y., Tian, Z., Nolte, S., Krooss, B. & Wang, M. 2022 An improved straight-line method for permeability and porosity determination for tight reservoirs using pulse-decay measurements. J. Nat. Gas Sci. Engng 105, 104708.CrossRefGoogle Scholar
Wang, Z., Wang, M. & Chen, S. 2018 Coupling of high Knudsen number and non-ideal gas effects in microporous media. J. Fluid Mech. 840, 56–72.CrossRefGoogle Scholar
Wood, B.D., He, X. & Apte, S.V. 2020 Modeling turbulent flows in porous media. Annu. Rev. Fluid Mech. 52, 171–203.CrossRefGoogle Scholar
Wu, Y.-S. & Pruess, K. 1998 Gas flow in porous media with Klinkenberg effects. Transp. Porous Media 32, 117–137.CrossRefGoogle Scholar
Zohar, Y., Lee, S.Y.K., Lee, W.Y., Jiang, L. & Tong, P. 2002 Subsonic gas flow in a straight and uniform microchannel. J. Fluid Mech. 472, 125–151.CrossRefGoogle Scholar