Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T21:12:34.056Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial wave rays in rotating spherical fluid domains

Published online by Cambridge University Press:  10 October 2014

Anna Rabitti  and
Leo R. M. Maas
Anna Rabitti*
Affiliation:
Department of Physical Oceanography, NIOZ Royal Netherlands Institute for Sea Research, PO Box 59, 1790 AB Texel, The Netherlands
Leo R. M. Maas
Affiliation:
Department of Physical Oceanography, NIOZ Royal Netherlands Institute for Sea Research, PO Box 59, 1790 AB Texel, The Netherlands
*
†Email address for correspondence: anna.rabitti@nioz.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

The behaviour of inertial waves in a rotating spherical container, filled with homogeneous fluid, is here investigated by means of a three-dimensional ray tracing algorithm, in a linear, inviscid framework. In particular, the classical, two-dimensional association between regular modes and periodic trajectories is addressed here for the first time in a fully three-dimensional setting. Three-dimensional, repelling periodic trajectories are found and classified on the basis of the associated frequency and spatial structure, although associated frequencies are hardly reconcilable to Bryan’s (Proc. R. Soc. Lond., vol. 45, 1889, pp. 42–45) classical solutions for inertial waves in the sphere. The normalized squared frequency 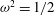$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\omega ^2 = 1/2$ appears to divide the frequency range into two different trajectory regimes, where critical latitudes play a different role. Chaotic orbits are not found, as expected, while invariant, non-domain-filling orbits (whispering gallery modes) constitute the majority of the trajectories in the sphere. From ray tracing alone, the wavefield is still far from being completely reconstructed, and a study performed in such a simplified setting is clearly far from any realistic application, however, it appears that three-dimensional ray dynamics constitutes a valid approach to infer information on the spectrum and regularity properties of a system, and is then able to bring new insight in a variety of fundamental problems of geophysical and astrophysical relevance, once its power and limitations have been recognized.

JFM classification

Mathematical Foundations: General fluid mechanics Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 758 , 10 November 2014 , pp. 621 - 654
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldridge, K. D. & Toomre, A. 1969 Axisymmetric inertial oscillations of a fluid in a rotating spherical container. J. Fluid Mech. 37, 307–323.Google Scholar
Arras, P., Flanagan, E. E., Morsink, S. M., Schenk, A. K., Teukolsky, S. A. & Wasserman, I. 2003 Saturation of the $r$ -mode instability. Astrophys. J. 591, 1129–1151.Google Scholar
Baines, P. G. 1971 The reflexion of internal/inertial waves from bumpy surfaces. J. Fluid Mech. 46, 273–292.Google Scholar
Barbosa Aguiar, A. C., Read, P. L., Wordsworth, R. D., Salter, T. & Hiro Yamazaki, Y. 2010 A laboratory model of Saturn’s North Polar Hexagon. Icarus 206 (2), 755–763.Google Scholar
Barcilon, V. 1968 Axi-symmetric inertial oscillations of a rotating ring of fluid. Mathematika 93, 93–102.Google Scholar
Baruteau, C. & Rieutord, M. 2013 Inertial waves in a differentially rotating spherical shell. J. Fluid Mech. 719, 47–81.Google Scholar
Berry, M. V. 1981 Regularity and chaos in classical mechanics, illustrated by the three deformations of a circular ‘billiad’. Eur. J. Phys. 2, 91–102.Google Scholar
Berry, M. V. 1987 Quantum chaology. Proc. R. Soc. Lond. A 413, 42–45.Google Scholar
Broutman, D., Rottman, J. W. & Eckermann, S. D. 2004 Ray methods for internal waves in the atmosphere and ocean. Annu. Rev. Fluid Mech. 36 (1), 233–253.Google Scholar
Bryan, G. H. 1889 The waves on a rotating liquid spheroid of finite ellipticity. Proc. R. Soc. Lond. 45, 42–45.Google Scholar
Cartan, M. E. 1922 Sur les petites oscillations d’une masse de fluide. Bull. Sci. Math. 46, 317–369.Google Scholar
Dintrans, B. & Ouyed, R. 2001 On Jupiter’s inertial mode oscillations. Astron. Astrophys. 375 (L47), 1–4.Google Scholar
Dintrans, B., Rieutord, M. & Valdettaro, L. 1999 Gravito-inertial waves in a rotating stratified sphere or spherical shell. J. Fluid Mech. 398, 271–297.Google Scholar
Drijfhout, S. & Maas, L. R. M. 2007 Impact of channel geometry and rotation on the trapping of internal tides. J. Phys. Oceanogr. 37 (11), 2740–2763.Google Scholar
Eckart, C. 1960 Hydrodynamics of Oceans and Atmospheres. Pergamon.Google Scholar
Eriksen, C. C. 1985 Implications of ocean bottom reflection for internal wave spectra and mixing. J. Phys. Oceanogr. (15), 1145–1156.Google Scholar
Favier, B., Barker, A. J., Baruteau, C. & Ogilvie, G. I. 2014 Nonlinear evolution of tidally forced inertial waves in rotating fluid bodies. Mon. Not. R. Astron. Soc. 439 (1), 845–860.Google Scholar
Gilbert, D. & Garrett, C. 1989 Implications for ocean mixing of internal wave scattering off irregular topography. J. Phys. Oceanogr. (19), 1716–1729.Google Scholar
Godfrey, D. A. 1988 A hexagonal feature around Saturn’s north pole. Icarus 76 (2), 335–356.Google Scholar
Görtler, H. 1943 Uber eine schwingungserscheinung in flussigkeiten mit stabiler dichteschichtung. Z. Angew. Math. Mech. 23, 65–71.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Gutzwiller, M. C. 1990 Chaos in Classical and Quantum Mechanics. Springer.Google Scholar
Harlander, U. & Maas, L. R. M. 2006 Characteristics and energy rays of equatorially trapped, zonally symmetric internal waves. Meteorol. Z. 15 (4), 439–450.Google Scholar
Harlander, U. & Maas, L. R. M. 2007 Internal boundary layers in a well-mixed equatorial atmosphere/ocean. Dyn. Atmos. Oceans 44 (1), 1–28.Google Scholar
Hazewinkel, J., Grisouard, N. & Dalziel, S. B. 2010 Comparison of laboratory and numerically observed scalar fields of an internal wave attractor. Eur. J. Mech. (B/Fluids) 30, 51–56.Google Scholar
Hazewinkel, J., Maas, L. R. M. & Dalziel, S. B. 2011 Tomographic reconstruction of internal wave patterns in a paraboloid. Exp. Fluids 50, 247–258.Google Scholar
Hazewinkel, J., Van Breevoort, P., Dalziel, S. B. & Maas, L. R. M. 2008 Observations on the wavenumber spectrum and evolution of an internal wave attractor. J. Fluid Mech. 598, 373–382.Google Scholar
Heller, E. J. 1984 Bound-state eigenfunctions of classically chaotic Hamiltonian systems: scars of periodic orbits. Phys. Rev. Lett. 53, 1515–1518.Google Scholar
Høiland, E. 1962 Discussion of a hyperbolic equation relating to inertia and gravitational fluid oscillations. Geophys. Publ. 26, 211–227.Google Scholar
Hollerbach, R., Futterer, B., More, T. & Egbers, C. 2004 Instabilities of the Stewartson layer part 2. Supercritical mode transitions. Theor. Comput. Fluid Dyn. 18, 197–204.Google Scholar
Hughes, B. 1964 Effect of rotation on internal gravity waves. Nature 201 (4921), 798–801.CrossRefGoogle Scholar
Ivanov, P. B. & Papaloizou, J. C. B. 2010 Inertial waves in rotating bodies: a WKBJ formalism for inertial modes and a comparison with numerical results. Mon. Not. R. Astron. Soc. 407 (3), 1609–1630.Google Scholar
John, F. 1941 The Dirichlet problem for hyperbolic equation. Am. J. Maths 63, 141–154.Google Scholar
Lord Kelvin, 1877 On the precessional motion of a liquid. Nature 15, 297–298.Google Scholar
Lord Kelvin, 1880a On an experimental illustration of minimum energy. Nature 23, 69–70.Google Scholar
Lord Kelvin, 1880b Vibrations of a columnar vortex. Phil. Mag. (10), 155–168.Google Scholar
Koch, S., Harlander, U., Egbers, C. & Hollerbach, R. 2013 Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results. Fluid Dyn. Res. 45 (3), 35504.Google Scholar
Kudlick, M. D.1966 On Transient Motions in a Contained Rotating Fluid. PhD thesis, Math. Dept., MIT.Google Scholar
Kudrolli, A., Abraham, M. C. & Gollub, J. P. 2001 Scarred patterns in surface waves. Phys. Rev. E 63 (2), 1–8.CrossRefGoogle ScholarPubMed
Le Bars, M., Le Dizès, S. & Le Gal, P. 2007 Coriolis effects on the elliptical instability in cylindrical and spherical rotating containers. J. Fluid Mech. 585, 323–342.Google Scholar
Lewis, B. M. & Hawkins, H. F. 1982 Polygonal eye walls and rainbands in hurricans. Bull. Am. Meteorol. Soc. 63 (11), 1294–1300.Google Scholar
Lockitch, K. H. & Friedman, J. L. 1999 Where are the $r$ -modes of isentropic stars? Astrophys. J. 521, 764–788.Google Scholar
Maas, L. R. M. 2003 On the amphidromic structure of inertial waves in a rectangular parallelepiped. Fluid Dyn. Res. 373, 373–401.Google Scholar
Maas, L. R. M. 2005 Wave attractors: linear yet nonlinear. Intl J. Bifurcation Chaos 15 (9), 2757–2782.Google Scholar
Maas, L. R. M., Benielli, D., Sommeria, J. & Lam, F.-P. A. 1997 Observation of an internal wave attractor in a confined, stably stratified fluid. Nature 388, 557–561.CrossRefGoogle Scholar
Maas, L. R. M. & Lam, F.-P. A. 1995 Geometric focusing of internal waves. J. Fluid Mech. 300, 1–41.Google Scholar
Manders, A. M. M. & Maas, L. R. M. 2004 On the three-dimensional structure of the inertial wavefield in a rectangular basin with one sloping boundary. Fluid Dyn. Res. 35, 1–21.Google Scholar
Münnich, M. 1996 The influence of bottom topography on internal seiches in stratified media. Dyn. Atmos. Oceans 23, 257–266.Google Scholar
Nöckel, J. U.1997 Resonances in nonintegrable open systems. PhD thesis, Yale University.Google Scholar
Nöckel, J. U., Stone, A. D., Chen, G., Grossman, H. L. & Chang, R. K. 1996 Directional emission from asymmetric resonant cavities. Opt. Lett. 21, 1609–1611.Google Scholar
Noir, J., Brito, D., Aldridge, K. & Cardin, P. 2001 Experimental evidence of inertial waves in a precessing spheroidal cavity. Geophys. Res. Lett. 28 (19), 3785.Google Scholar
Nurijanyan, S., Bokhove, O. & Maas, L. R. M. 2013 A new semi-analytical solution for inertial waves in a rectangular parallelepiped. Phys. Fluids 25 (12), 126601.Google Scholar
Ogilvie, G. I. 2005 Wave attractors and the asymptotic dissipation rate of tidal disturbances. J. Fluid Mech. 543, 19–44.Google Scholar
Ogilvie, G. I. & Lin, D. N. C. 2004 Tidal dissipation in rotating giant planets. Astrophys. J. 610, 477–509.Google Scholar
Phillips, O. M. 1963 Energy transfer in rotating fluids by reflection of inertial waves. Phys. Fluids 6, 513–520.Google Scholar
Rabitti, A. & Maas, L. R. M. 2013 Meridional trapping and zonal propagation of inertial waves in a rotating fluid shell. J. Fluid Mech. 729, 445–470.Google Scholar
Rieutord, M. 1991 Linear theory of rotating fluids using spherical harmonics part II, time-periodic flows. Geophys. Astrophys. Fluid Dyn. 59, 185–208.Google Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2000 Wave attractors in rotating fluids: a paradigm for ill-posed Cauchy problems. Phys. Rev. Lett. 85 (20), 4277–4280.Google Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.Google Scholar
Rieutord, M., Valdettaro, L. & Georgeot, B. 2002 Analysis of singular inertial modes in a spherical shell: the slender toroidal shell model. J. Fluid Mech. 463, 345–360.Google Scholar
Scolan, H., Ermanyuk, E. & Dauxois, T. 2013 Nonlinear fate of internal wave attractors. Phys. Rev. Lett. 110 (23), 234501.Google Scholar
Stewartson, K. & Rickard, J. A. 1969 Pathological oscillations of a rotating fluid. J. Fluid Mech. 35, 759–773.Google Scholar
van Haren, H. & Gostiaux, L. 2012 Energy release through internal wave breaking. Oceanography 25 (2), 124–131.Google Scholar
Whitham, G. B. 1960 A note on group velocity. J. Fluid Mech. 9, 347–352.Google Scholar
Whitham, G. B. 1974 Linear and Non Linear Waves. John Wiley & Sons.Google Scholar
Wu, Y. 2005a Origin of tidal dissipation in Jupiter. I. Properties of inertial modes. Astrophys. J. 635, 674–687.CrossRefGoogle Scholar
Wu, Y. 2005b Origin of tidal dissipation in Jupiter. II. The value of $Q$ . Astrophys. J. 13, 688–710.Google Scholar
Wunsch, C. & Ferrari, R. 2004 Vertical mixing, energy, and the general circulation of the oceans. Annu. Rev. Fluid Mech. 36 (1), 281–314.Google Scholar
Zhang, K., Chan, K. H., Liao, X. & Aurnou, J. M. 2013 The non-resonant response of fluid in a rapidly rotating sphere undergoing longitudinal libration. J. Fluid Mech. 720, 212–235.Google Scholar
Zhang, K., Earnsahw, P., Liao, X. & Busse, F. H. 2001 On inertial waves in a rotating fluid sphere. J. Fluid Mech. 437, 103–119.Google Scholar