Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T06:37:55.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial-particle accelerations in turbulence: a Lagrangian closure

Published online by Cambridge University Press:  31 May 2016

S. Vajedi ,
K. Gustavsson ,
B. Mehlig  and
L. Biferale
S. Vajedi
Affiliation:
Department of Physics, Gothenburg University, SE-41296 Gothenburg, Sweden
K. Gustavsson
Affiliation:
Department of Physics, Gothenburg University, SE-41296 Gothenburg, Sweden Department of Physics and INFN, University of Rome ‘Tor Vergata’, Via della Ricerca Scientifica 1, 00133 Rome, Italy
B. Mehlig
Affiliation:
Department of Physics, Gothenburg University, SE-41296 Gothenburg, Sweden
L. Biferale*
Affiliation:
Department of Physics and INFN, University of Rome ‘Tor Vergata’, Via della Ricerca Scientifica 1, 00133 Rome, Italy
*
†Email address for correspondence: biferale@roma2.infn.it
Get access Rights & Permissions [Opens in a new window]

Abstract

The distribution of particle accelerations in turbulence is intermittent, with non-Gaussian tails that are quite different for light and heavy particles. In this article we analyse a closure scheme for the acceleration fluctuations of light and heavy inertial particles in turbulence, formulated in terms of Lagrangian correlation functions of fluid tracers. We compute the variance and the flatness of inertial-particle accelerations and we discuss their dependency on the Stokes number. The closure incorporates effects induced by the Lagrangian correlations along the trajectories of fluid tracers, and its predictions agree well with results of direct numerical simulations of inertial particles in turbulence, provided that the effects induced by inertial preferential sampling of heavy/light particles outside/inside vortices are negligible. In particular, the scheme predicts the correct functional behaviour of the acceleration variance, as a function of 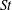$St$, as well as the presence of a minimum/maximum for the flatness of the acceleration of heavy/light particles, in good qualitative agreement with numerical data. We also show that the closure works well when applied to the Lagrangian evolution of particles using a stochastic surrogate for the underlying Eulerian velocity field. Our results support the conclusion that there exist important contributions to the statistics of the acceleration of inertial particles independent of the preferential sampling. For heavy particles we observe deviations between the predictions of the closure scheme and direct numerical simulations, at Stokes numbers of order unity. For light particles the deviation occurs for larger Stokes numbers.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 187 - 200
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alipchenkov, V. M. & Zaichik, L. I. 2007 Particle collisions in turbulent flows. Fluid Dyn. 42, 419–432.Google Scholar
Babiano, A., Cartwright, J. H. E., Piro, I. & Provenzale, A. 2000 Dynamics of a small neutrally buoyant sphere in a fluid and targeting in hamiltonian systems. Phys. Rev. Lett. 84, 5764–5767.CrossRefGoogle Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A., Musacchio, S. & Toschi, F. 2006a Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550, 349–358.CrossRefGoogle Scholar
Bec, J., Biferale, L., Boffetta, G., Cencini, M., Musacchio, S. & Toschi, F. 2006b Lyapunov exponents of heavy particles in turbulence. J. Fluid Mech. 18, 091702.Google Scholar
Bec, J., Biferale, L., Cencini, M., Lanotte, A., Musacchio, S. & Toschi, F. 2007 Heavy particle concentration in turbulence at dissipative and inertial scales. Phys. Rev. Lett. 98, 084502.CrossRefGoogle ScholarPubMed
Bec, J., Biferale, L., Cencini, M., Lanotte, A. & Toschi, F. 2010a Intermittency in the velocity distribution of heavy particles in turbulence. J. Fluid Mech. 646, 527–536.CrossRefGoogle Scholar
Bec, J., Biferale, L., Lanotte, A. S., Scagliarini, A. & Toschi, F. 2010b Turbulent pair dispersion of inertial particles. J. Fluid Mech. 645, 497.CrossRefGoogle Scholar
Bec, J., Celani, A., Cencini, M. & Musacchio, S. 2005 Clustering and collisions in random flows. Phys. Fluids 17, 073301.Google Scholar
Bec, J., Homann, H. & Ray, S. S. 2014 Gravity-driven enhancement of heavy particle clustering in turbulent. Phys. Rev. Lett. 112, 184501.Google Scholar
van den Berg, T., van Gils, D., Lathrop, D. & Lohse, D. 2007 Bubbly turbulent drag reduction is a boundary layer effect. Phys. Rev. Lett. 98, 084501.Google Scholar
van den Berg, T., Luther, S., Lathrop, D. & Lohse, D. 2005 Drag reduction in bubbly Taylor–Couette turbulence. Phys. Rev. Lett. 94, 044501.Google Scholar
Bragg, A. D. & Collins, L. R. 2014 New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distribution of particles. New J. Phys. 16, 055013.Google Scholar
Calzavarini, E., Cencini, M., Lohse, D. & Toschi, F. 2008a Quantifying turbulence-induced segregation of inertial particles. Phys. Rev. Lett. 101, 084504.CrossRefGoogle ScholarPubMed
Calzavarini, E., Kerscher, M., Lohse, D. & Toschi, F. 2008b Dimensionality and morphology of particle and bubble clusters in turbulent flow. J. Fluid Mech. 607, 13–24.Google Scholar
Calzavarini, E., Volk, R., Bourgoin, M., Leveque, E., Pinton, J. F. & Toschi, F. 2009 Acceleration statistics of finite-sized particles in turbulent flow: the role of Faxén forces. J. Fluid Mech. 630, 179.Google Scholar
Cencini, M., Bec, J., Biferale, L., Boffetta, G., Celani, A., Lanotte, A., Musacchio, S. & Toschi, F. 2006 Dynamics and statistics of heavy particles in turbulent flows. J. Turbulence 7, 1–16.Google Scholar
Chen, S., Doolen, G. D., Kraichnan, R. H. & She, Z. S. 1993 On statistical correlations between velocity increments and locally averaged dissipation in homogeneous turbulence. Phys. Fluids A 5, 458.CrossRefGoogle Scholar
Derevich, I. 2000 Statistical modelling of mass transfer in turbulent two-phase dispersed flow 1. Model development. Intl J. Heat Mass Transfer 43, 3709–3723.Google Scholar
Duncan, K., Mehlig, B., Östlund, S. & Wilkinson, M. 2005 Clustering in mixing flows. Phys. Rev. Lett. 95, 240602.CrossRefGoogle ScholarPubMed
Falkovich, G., Fouxon, A. & Stepanov, G. 2002 Acceleration of rain initiation by cloud turbulence. Nature 419, 151–154.Google Scholar
Falkovich, G. & Pumir, A. 2007 Sling effect in collisions of water droplets in turbulent clouds. J. Atmos. Sci. 64, 4497–4505.CrossRefGoogle Scholar
Falkovich, G., Xu, H., Pumir, A., Bodenschatz, E., Biferale, L., Boffetta, G., Lanotte, A. S. & Toschi, F. 2012 On lagrangian single-particle statistics. Phys. Fluids 24, 055102.Google Scholar
Ferry, J. & Balachandar, S. 2001 A fast Eulerian method for disperse two-phase flow. Intl J. Multiphase Flow 27, 1199–1226.CrossRefGoogle Scholar
Gibert, M., Xu, H. & Bodenschatz, E. 2010 Inertial effects on two-particle relative dispersion in turbulent flows. Europhys. Lett. 90, 64005.Google Scholar
Gibert, M., Xu, H. & Bodenschatz, E. 2012 Where do small weakly inertial particles go in a turbulent flow? J. Fluid Mech. 698, 160–167.Google Scholar
Goto, S. & Vassilicos, J. C. 2008 Sweep-stick mechanism of heavy particle clustering in turbulence. Phys. Rev. Lett. 100, 054503.CrossRefGoogle Scholar
Gustavsson, K. & Mehlig, B. 2011 Distribution of relative velocities in turbulent aerosols. Phys. Rev. E 84, 045304.Google Scholar
Gustavsson, K. & Mehlig, B. 2014 Relative velocities of inertial particles in turbulent aerosols. J. Turbul. 15, 34–69.Google Scholar
Gustavsson, K. & Mehlig, B. 2016 Statistical models for spatial patterns of heavy particles in turbulence. Adv. Phys. 64, 1–57.Google Scholar
Jacob, B., Olivieri, A., Miozzi, M., Campana, E. F. & Piva, R. 2010 Drag reduction by microbubbles in a turbulent boundary layer. Phys. Fluids 22, 115104.CrossRefGoogle Scholar
Mathai, V., Prakash, V., Brons, J., Sun, C. & Lohse, D. 2015 Wake-driven dynamics of finite-sized buyoant sphere in turbulence. Phys. Rev. Lett. 115, 124501.CrossRefGoogle Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Mazzitelli, I. M., Lohse, D. & Toschi, F. 2003 The effect of microbubbles on developed turbulence. Phys. Fluids 15, L5.Google Scholar
Pan, L. & Padoan, P. 2010 Relative velocity of inertial particles in turbulent flows. J. Fluid Mech. 661, 73.Google Scholar
Prakash, V. N., Tagawa, Y., Calzavarini, E., Mercado, J. M., Toschi, F., Lohse, D. & Sun, C. 2012 How gravity and size affect the acceleration statistics of bubbles in turbulence. New. J. Phys. 14, 105017.Google Scholar
Qureshi, N. M., Arrieta, U., Baudet, C., Cartellier, A., Gagne, Y. & Bourgoin, M. 2008 Acceleration statistics of inertial particles in turbulent flow. Eur. Phys. J. B 66, 531.Google Scholar
Rensen, J., Luther, S. & Lohse, D. 2005 The effect of bubbles on developed turbulence. J. Fluid Mech. 538, 153.CrossRefGoogle Scholar
Shaw, R. A. 2003 Particle-turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35, 183–207.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. J. Fluid. Mech. 335, 75–109.Google Scholar
Tchen, C. M.1947 Mean values and correlation problems connected with the motion of small particles suspended in a turbulent fluid. PhD thesis, TU Delft.Google Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.Google Scholar
Volk, R., Calzavarini, E., Leveque, E. & Pinton, J. F. 2011 Dynamics of inertial particles in a turbulent von Kármán flow. J. Fluid Mech. 668, 223.Google Scholar
Volk, R., Calzavarini, E., Verhille, G., Lohse, D., Mordant, N., Pinton, J.-F. & Toschi, F. 2008 Acceleration of heavy and light particles in turbulence: comparison between experiments and direct numerical simulations. Physica D 237, 2084–2089.Google Scholar
Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71, 186–192.CrossRefGoogle Scholar
Wilkinson, M., Mehlig, B. & Bezuglyy, V. 2006 Caustic activation of rain showers. Phys. Rev. Lett. 97, 048501.CrossRefGoogle ScholarPubMed
Zaichik, L. & Alipchenkov, V. 2003 Pair dispersion and preferential concentration of particles in isotropic turbulence. Phys. Fluids 15, 1776–1787.Google Scholar