Published online by Cambridge University Press: 17 June 2020
The influence of fluid–structure interaction on cloud cavitation about a hydrofoil is investigated by comparing results from a relatively stiff reference hydrofoil, presented in Part 1, with those obtained on a geometrically identical flexible hydrofoil. Measurements were conducted with a chord-based Reynolds number  $Re=0.8\times 10^{6}$ for cavitation numbers,
$Re=0.8\times 10^{6}$ for cavitation numbers,  $\unicode[STIX]{x1D70E}$, ranging from 0.2 to 1.2 while the hydrofoil was mounted at an incidence,
$\unicode[STIX]{x1D70E}$, ranging from 0.2 to 1.2 while the hydrofoil was mounted at an incidence,  $\unicode[STIX]{x1D6FC}$, of
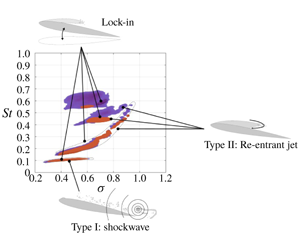
$\unicode[STIX]{x1D6FC}$, of  $6^{\circ }$ to the oncoming flow. Tip deformations and cavitation behaviour were recorded with synchronised force measurements utilising two high-speed cameras. The flexible composite hydrofoil was manufactured as a carbon/glass-epoxy hybrid structure with a lay-up sequence selected principally to consider spanwise bending deformations with no material-induced bend–twist coupling. Hydrodynamic bend–twist coupling is seen to result in nose-up twist deformations causing frequency modulation from the increase in cavity length. The lock-in phenomenon driven by re-entrant jet shedding observed on the stiff hydrofoil is also evident on the flexible hydrofoil at
$6^{\circ }$ to the oncoming flow. Tip deformations and cavitation behaviour were recorded with synchronised force measurements utilising two high-speed cameras. The flexible composite hydrofoil was manufactured as a carbon/glass-epoxy hybrid structure with a lay-up sequence selected principally to consider spanwise bending deformations with no material-induced bend–twist coupling. Hydrodynamic bend–twist coupling is seen to result in nose-up twist deformations causing frequency modulation from the increase in cavity length. The lock-in phenomenon driven by re-entrant jet shedding observed on the stiff hydrofoil is also evident on the flexible hydrofoil at  $0.70\leqslant \unicode[STIX]{x1D70E}\leqslant 0.75$, but occurs between different modes. Flexibility is observed to accelerate cavitation regime transition with reducing
$0.70\leqslant \unicode[STIX]{x1D70E}\leqslant 0.75$, but occurs between different modes. Flexibility is observed to accelerate cavitation regime transition with reducing  $\unicode[STIX]{x1D70E}$. This is seen with the rapid growth and influence the shockwave instability has on the forces, deflections and cavitation behaviour on the flexible hydrofoil, suggesting structural behaviour plays a significant role in modifying cavity physics. The reduced stiffness causes secondary lock-in of the flexible hydrofoil’s one-quarter sub-harmonic,
$\unicode[STIX]{x1D70E}$. This is seen with the rapid growth and influence the shockwave instability has on the forces, deflections and cavitation behaviour on the flexible hydrofoil, suggesting structural behaviour plays a significant role in modifying cavity physics. The reduced stiffness causes secondary lock-in of the flexible hydrofoil’s one-quarter sub-harmonic,  $f_{n}/4$, at
$f_{n}/4$, at  $\unicode[STIX]{x1D70E}$ = 0.4. This leads to the most severe deflections observed in the conditions tested along with a shift in phase between normal force and tip deflection.
$\unicode[STIX]{x1D70E}$ = 0.4. This leads to the most severe deflections observed in the conditions tested along with a shift in phase between normal force and tip deflection.
At σ = 1.20, the flexible hydrofoils increased effective incidence due to twist deformations causes cavity break-up to interchange between interfacial instabilities and re-entrant jet formation over time on the flexible hydrofoil. Small scale vapour structures can be seen shedding from positions along the span due to re-entrant jet formation which is only observed on the stiff hydrofoil once σ is reduced to 1.0. The cavity is also seen to still be broken up to due to inter-facial instabilities such as Kelvin-Helmholtz driven spanwise vorticity lines and turbulent transition.
At σ = 1.00, the flexible hydrofoil is experiencing Type IIa shedding where the re-entrant jet mechanism is confined to around mid-span due to three-dimensional flows effects as mentioned in part 1. Shedding is seen to occur at approximately St = 0.61 which is lower compared to the stiff hydrofoil which experiences shedding at St =74.
Reduction in σ down to 0.8 sees the cavity along with the re-entrant jet thickness grow, giving it enough momentum to overcome spanwise flow components and reach the leading edge for majority of the span. This results in the formation of two shedding sites with the Type IIa and IIb modes both active.
Further reduction in σ to 0.7 sees the hydrofoil enter lock-in where the Type IIb tip shedding frequency matches the first mode of the hydrofoil leading to amplified structural excitations. The Type IIa shedding is still evident in the upper portion of the span while the Type IIb shedding events in the lower span are more defined to that occurring on the stiff hydrofoil due to FSI.
As σ reaches 0.65, the attached cavity now extends to the trailing edge causing the cloud cavitation to no longer have spanwise compatibility with the hydrofoil, leading to irregular shedding along the span. The extended cavity lengths reaching the trailing edge leads to the formation of shockwaves with both the re-entrant jet and shockwave mechanisms influencing shedding. Small scale break-up of the cavity from surface perturbations forming as the re-entrant jet moves upstream preconditions the flow for condensation shockwaves to form. Similar to the stiff hydrofoil, the shockwave causes the shedding of cloud cavitation where the re-entrant jet instability drives the frequency. However, due in increased FSI, the emergence of the shockwave instability is accelerated on the flexible hydrofoil with similar behaviour seen between the stiff hydrofoil at σ = 0.60 and the flexible at σ = 0.65.
With σ reducing to 0.55, the cavitation behavior becomes highly irregular with both the re-entrant jet and shockwave instability active as well as a lack of spanwise compatibility between the attached cavity and the hydrofoil. Strong interactions between the deforming hydrofoil, attached cavity and multiple shedding mechanisms results in highly complex cavitation behavior.
At σ = 0.5 the attached cavity appears more perturbed on the flexible hydrofoil than that of the stiff. This results in small-scale cavity break-up increasing the bubble population in the flow and hence, activating the shockwave instability at a higher σ as well as increasing its severity. The re-entrant jet is still evident in the flow, however, the shockwave instability dominates the cavity dynamics.
At σ = 0.4, due to FSI, the flexible hydrofoil experiences solely shockwave driven shedding before the stiff hydrofoil. A re-entrant jet still forms but lacks sufficient time and momentum to reach the upstream extent of the cavity. This results in the shockwave driving the shedding frequency at a rate of St = 0.11 where unlike on the stiff hydrofoil with multiple shedding events in a cycle, the flexible hydrofoil experience full span coherent shedding.