Article contents
The influence of inertia on the rheology of a periodic suspension of neutrally buoyant rigid ellipsoids
Published online by Cambridge University Press: 24 September 2015
Abstract
We investigate the rheological properties of a suspension of neutrally buoyant rigid ellipsoids by fluid–structure interaction simulations of a particle in a periodic domain under simple shear using the curvilinear immersed-boundary (CURVIB) method along with a quaternion–angular velocity technique to calculate the dynamics of the particle’s motion. We calculate all the different terms of particle stress for the first time for non-spherical particles, i.e. in addition to the stresslet, we calculate the acceleration and Reynolds stress, which are typically ignored in previous similar works. Furthermore, we derive analytical expressions for all these terms to verify the numerical results and deduce the effect of inertia by comparing our numerical results with the analytical solution. The effect of particle Reynolds number (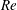 $\mathit{Re}$), volume fraction (
$\mathit{Re}$), volume fraction (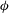 ${\it\phi}$), and the shape of particles has been studied on all mechanisms of stress generation, the intrinsic viscosity, and normal stress differences of the suspension for the range
${\it\phi}$), and the shape of particles has been studied on all mechanisms of stress generation, the intrinsic viscosity, and normal stress differences of the suspension for the range 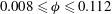 $0.008\leqslant {\it\phi}\leqslant 0.112$ and
$0.008\leqslant {\it\phi}\leqslant 0.112$ and 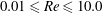 $0.01\leqslant \mathit{Re}\leqslant 10.0$. We found that inertia increases the shear and the second normal difference of the stresslet (dominant term of the particle stress), and decreases the first normal difference that is generated due to the strain field. The contribution of acceleration stress to the total stress is found to be important in the second normal stress difference, with a cycle-average comparable to the stresslet component. We also discovered that the contribution of Reynolds stress in the first normal stress difference becomes important even when inertia is as low as
$0.01\leqslant \mathit{Re}\leqslant 10.0$. We found that inertia increases the shear and the second normal difference of the stresslet (dominant term of the particle stress), and decreases the first normal difference that is generated due to the strain field. The contribution of acceleration stress to the total stress is found to be important in the second normal stress difference, with a cycle-average comparable to the stresslet component. We also discovered that the contribution of Reynolds stress in the first normal stress difference becomes important even when inertia is as low as 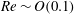 $\mathit{Re}\sim O(0.1)$, and its value can be even greater than the stresslet when inertia increases, i.e. Reynolds stresses cannot be ignored for non-spherical particles. For concentrations in the range from dilute to semi-dilute, the effect of inertia on the intrinsic viscosity of a suspension is found to be comparable to the volume fraction. Furthermore, our calculations show that for a dilute concentration and the low-inertia regime (
$\mathit{Re}\sim O(0.1)$, and its value can be even greater than the stresslet when inertia increases, i.e. Reynolds stresses cannot be ignored for non-spherical particles. For concentrations in the range from dilute to semi-dilute, the effect of inertia on the intrinsic viscosity of a suspension is found to be comparable to the volume fraction. Furthermore, our calculations show that for a dilute concentration and the low-inertia regime (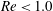 $\mathit{Re}<1.0$), the intrinsic viscosity of a suspension consisting of ellipsoids with an aspect ratio of five can be 20 % higher than its Stokesian analytical value.
$\mathit{Re}<1.0$), the intrinsic viscosity of a suspension consisting of ellipsoids with an aspect ratio of five can be 20 % higher than its Stokesian analytical value.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 20
- Cited by


