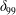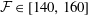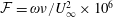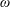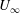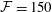Influence of localised smooth steps on the instability of a boundary layer

Abstract

We consider a smooth, spanwise-uniform forward-facing step defined by a Gauss error function of height 4 %–30 % and four times the width of the local boundary layer thickness $\unicode[STIX]{x1D6FF}_{99}$ . The boundary layer flow over a smooth forward-facing stepped plate is studied with particular emphasis on stabilisation and destabilisation of the two-dimensional Tollmien–Schlichting (TS) waves and subsequently on three-dimensional disturbances at transition. The interaction between TS waves at a range of frequencies and a base flow over a single or two forward-facing smooth steps is conducted by linear analysis. The results indicate that for a TS wave with a frequency ${\mathcal{F}}\in [140,160]$ ( ${\mathcal{F}}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/U_{\infty }^{2}\times 10^{6}$ , where $\unicode[STIX]{x1D714}$ and $U_{\infty }$ denote the perturbation angle frequency and free-stream velocity magnitude, respectively, and $\unicode[STIX]{x1D708}$ denotes kinematic viscosity), the amplitude of the TS wave is attenuated in the unstable regime of the neutral stability curve corresponding to a flat plate boundary layer. Furthermore, it is observed that two smooth forward-facing steps lead to a more acute reduction of the amplitude of the TS wave. When the height of a step is increased to more than 20 % of the local boundary layer thickness for a fixed width parameter, the TS wave is amplified, and thereby a destabilisation effect is introduced. Therefore, the stabilisation or destabilisation effect of a smooth step is typically dependent on its shape parameters. To validate the results of the linear stability analysis, where a TS wave is damped by the forward-facing smooth steps direct numerical simulation (DNS) is performed. The results of the DNS correlate favourably with the linear analysis and show that for the investigated frequency of the TS wave, the K-type transition process is altered whereas the onset of the H-type transition is delayed. The results of the DNS suggest that for the perturbation with the non-dimensional frequency parameter ${\mathcal{F}}=150$ and in the absence of other external perturbations, two forward-facing smooth steps of height 5 % and 12 % of the boundary layer thickness delayed the H-type transition scenario and completely suppressed for the K-type transition. By considering Gaussian white noise with both fixed and random phase shifts, it is demonstrated by DNS that transition is postponed in time and space by two forward-facing smooth steps.

1 Introduction

1.1 Motivation behind the study of steps in boundary layers

In environments with low levels of disturbances, transition to turbulence is initiated by the exponential amplification of the Tollmien–Schlichting (TS) waves followed by the growth of secondary instabilities. When the r.m.s. amplitude of the TS waves exceeds a threshold value of typically $1\,\%$ of the free-stream velocity, three-dimensional (3D) structures evolve, which are characterized by nearly periodic spanwise alternating peaks and valleys ( $\unicode[STIX]{x1D6EC}$ -shaped vortex loop) (Herbert 1988; Cossu & Brandt 2002). Growth of these 3D structures is very rapid (over a convective time scale), which is explained by secondary instability theory. Fundamental and subharmonic instabilities lead respectively to aligned and staggered patterns of $\unicode[STIX]{x1D6EC}$ -structures. Because of the dramatic growth of the 3D disturbances, nonlinear deformation of the flow field produces embedded highly inflectional instantaneous velocity profiles. The highly inflectional instantaneous velocity profiles are unstable with respect to high-frequency disturbances that cause spikes (intensive streamwise velocity fluctuation; Klebanoff, Tidstrom & Sargent 1962). The onset of spikes initiates the ultimate breakdown of the laminar flow into turbulence. This path to transition was explained by Herbert (1988) and more recently by Cossu & Brandt (2004).

The classical process of the laminar–turbulent transition is subdivided into three stages: receptivity, linear eigenmode growth and nonlinear breakdown to turbulence. A long-standing goal of laminar flow control (LFC) is the development of drag-reduction mechanisms by delaying the onset of transition. The process of laminar to turbulent transition has been shown to be influenced by many factors, such as surface roughness elements, slits, surface waviness and steps. These surface imperfections can significantly influence the laminar–turbulent transition by influencing the growth of TS waves in accordance with linear stability theory and then nonlinear breakdown along with 3D effects (Kachanov 1994). Since the existence of TS waves was confirmed by Schubauer & Skramstad (1948), numerous studies aiming to stabilise or destabilise the TS modes have been carried out in order to explore and explain different paths to transition. If the growth of the TS waves is reduced or completely suppressed, and providing no other instability mechanism comes into play, it has been suggested transition could be postponed or even eliminated (Davies & Carpenter 1996). Despite roughness elements being traditionally seen as an impediment to the stability of the flat plate boundary layer, recent research has shown this might not always be the case. Reibert et al. (1996) used spanwise-periodic discrete roughness elements to excite the most unstable wave and found unstable waves occur only at integer multiples of the primary disturbance wavenumber and no subharmonic disturbances are destabilised. Following this research, Saric, Carrillo & Reibert (1998) continued to investigate the effect of spanwise-periodic discrete roughness whose primary disturbance wavenumber did not contain a harmonic at $\unicode[STIX]{x1D706}_{s}=12$  mm (the most unstable wavelength according to linear theory, where $\unicode[STIX]{x1D706}_{s}$ denotes the crossflow disturbance wavelength in the spanwise direction). By changing the forced fundamental disturbance wavelength to 18 mm, the 18, 9 and 6 mm wavelengths were present. Saric et al. (1998) found the linearly most unstable disturbance (12 mm) was completely suppressed. Shahinfar et al. (2012) showed that classical vortex generators, known for their efficiency in delaying, or even inhibiting, boundary layer separation can be equally effective in delaying transition. An array of miniature vortex generator (MVGs) was shown experimentally to strongly damp TS waves at a frequency ${\mathcal{F}}=\unicode[STIX]{x1D714}\unicode[STIX]{x1D708}/U_{\infty }^{2}\times 10^{6}=102$ (where $\unicode[STIX]{x1D714}$ and $U_{\infty }$ denote the perturbation angle frequency and free-stream velocity magnitude, respectively, and  $\unicode[STIX]{x1D708}$ denotes kinematic viscosity) and delay the onset of transition. Similar results were obtained for ${\mathcal{F}}=135$ and 178. Downs & Fransson (2014) found that the amplitudes of TS wave ${\mathcal{F}}\in \{100,110,120,130\}$ over spanwise periodic surface patterns can be reduced, and demonstrated substantial delays in the onset of transition when TS waves are forced with large amplitudes.

Over the past two decades, most investigations on topics of laminar–turbulent transition in a boundary layer have focused on two kinds of problem: the receptivity mechanism (Wu 2001a , b ; Saric, Reed & Kerschen 2002; Ruban, Bernots & Pryce 2013) and stabilisation/destabilisation of TS waves (Cossu & Brandt 2002, 2004; Fransson et al. 2005, 2006; Garzon & Roberts 2013). Meanwhile, we need to point out that TS waves are important basically in two-dimensional (2D) subsonic boundary-layers on flat or convex surfaces, while in many other cases other instabilities dominate and are being extensively investigated. In contrast to the 2D case, the 3D boundary layer exhibits both streamwise and crossflow components. The study of flow stability in boundary layers with transverse pressure gradients is traced back to the experiments of Gray (1952). An early review work on crossflow is attributed to Reed & Saric (1989) and a more recent review on crossflow instability was made by Saric, Reed & White (2003). In 2D boundary layer flows over concave walls, Görtler vortices are thought to be the cause of transition (Saric 1994). In order to improve our understanding of the underpinning role of TS waves we choose to focus our attention on their effect by leveraging the fact that DNS investigation allows us to neglect other forms of perturbation. Therefore this case is not intended to be representative of the richer transition scenario on an actual aircraft wing cruising in a natural environment.

Receptivity is the initial stage of the uncontrolled (‘natural’) transition process, first highlighted by Morkovin (1969a ), where environmental disturbances, such as acoustic waves or vorticity, are transformed into smaller-scale perturbations within the boundary layer (Morkovin 1969b ). For an uncontrolled transition process, these disturbances may initially be too small to measure, and are observed only after the onset of an instability, and the nature of the basic state and the growth (or decay) of these disturbances depends on the nature of the disturbance (Saric et al. 2002). The aim of receptivity studies is to assess the initial condition of the disturbance amplitude, frequency and phase within the boundary (Morkovin 1969b ; Saric et al. 2002). So far, only a small fraction of various possible receptivity mechanisms has been investigated for the cases of either: (i) direct excitation of stationary instability modes (such as crossflow or Görlter modes) by stationary surface roughness or (ii) transformation of various unsteady external disturbances (such as various free-stream vortices, acoustic waves, etc.) on various 2D and 3D streamwise-localised surface roughness elements resulting in excitation of various 2D and 3D non-stationary instability modes (such as TS modes, crossflow modes, Görtler modes, etc.) (Gaster 1965; Murdock 1980; Goldstein 1983; Ruban 1984; Goldstein 1985; Goldstein & Hultgren 1987; Kerschen 1989, 1990; Hall 1990; Denier, Hall & Seddougui 1991; Bassom & Hall 1994; Choudhari 1994; Saric 1994; Bassom & Seddougui 1995; Duck, Ruban & Zhikharev 1996; Dietz 1999; Wu 2001b ; Saric et al. 2002; Templelmann 2011). The receptivity mechanism shows that the deviation on the length scale of eigenmodes from a smooth surface can excite TS waves by interacting with free-stream disturbances or acoustic noise. Kachanov, Kozlov & Levchenko (1979a ), Kachanov et al. (1979b ) first performed the quantitative experimental study of the boundary layer receptivity to unsteady free-stream vortices for the case of a 2D problem with the spanwise orientation of the disturbance vorticity vector. The result of Kachanov et al. (1979a , b ) was consistent with the theoretical study by Rogler & Reshotko (1975). Considering steady vortices, Kendall (1985, 1990, 1991) obtained the first qualitative data, which was compared with numerical results generated by Bertolotti (1996, 2003).

From a theoretical point of view, Ruban (1984), Goldstein (1985), Goldstein & Hultgren (1987), Duck et al. (1996) studied the interactions of free-stream disturbances with an isolated steady hump within the viscous sublayer of a triple-deck region. As indicated by Borodulin et al. (2013), almost all investigations related to unsteady vortex receptivity of boundary layers performed after the early experiments were theoretical ones until the end of the 1990s. For distributed roughness receptivity, considering a weak waviness, Zavol’skii, Reutov & Rybushkina (1983) theoretically investigated the problem of resonant scattering of a periodical vortex street on a wall, based on the framework of a locally parallel theory. Subsequently, the theoretical approach was developed by Choudhari & Streett (1992) and Crouch (1994) for localised and distributed vortex receptivity. Based on asymptotic theory, Goldstein (1983, 1985), Ruban (1985) and Wu (2001a ) carried out the studies for acoustic receptivity and Kerschen (1990), Goldstein & Leib (1993), Choudhari (1994) and Wu (2001a , b ) for localised and distributed boundary layer receptivity. A detailed review work was done in the introduction of Borodulin et al. (2013).

However, theoretical studies of the interaction between instability modes and a distorted base flow have received less attention. For distributed roughness Corke, Sever & Morkovin (1986) further inferred that the faster growth of TS waves on the rough wall was not attributable to the destabilization effect of roughness, such as an inflectional instability, but claimed that the growth was due to the continual excitation of TS waves on the rough wall by free-stream turbulence. More recently, important theoretical work on the interaction of isolated roughness with either acoustic or vortical free-stream disturbances was investigated by Wu & Hogg (2006). Brehm et al. (2011) investigated the impact of 2D distributed roughness on the laminar–turbulent transition process, and found that the roughness spacing has a drastic effect on the growth of disturbances. Borodulin et al. (2013) discussed the influence of distributed mechanisms on amplification of instability modes. As indicated by Brehm et al. (2011), for isolated roughness some basic understanding of the physical mechanisms promoting transition has been obtained, but the relevant physical mechanisms driving the transition process in the presence of distributed roughness are not well understood.

In this paper, we investigate the effect of a smooth forward-facing step on the growth properties of TS waves excited by forcing the boundary layer at different unstable non-dimensional frequencies. The amplitude of the forcing was chosen such that the velocity profiles of the resulting TS waves are well resolved but weak enough such that no secondary instabilities are introduced. For the domain of the flat plate considered in the test cases presented here the unstable frequencies span ${\mathcal{F}}\in [27,250]$ for displacement thickness Reynolds number $Re_{\unicode[STIX]{x1D6FF}^{\ast }}\in [320,1500]$ ( $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=U_{\infty }\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D708}$ , where $U_{\infty }$ and $\unicode[STIX]{x1D708}$ denote streamwise free-stream velocity magnitude and kinematic viscosity, respectively, and $\unicode[STIX]{x1D6FF}^{\ast }$ denotes the displacement thickness). We denote frequencies as high for ${\mathcal{F}}\in [100,250]$ . These high-frequencies are of particular interest because they can lead to transition towards the leading edge of the flat plate (Downs & Fransson 2014). Note, the difference between the smooth step considered in this paper and a traditional sharp step is that the geometry for a smooth step is described by no less than two parameters (height and width) whereas for a traditional sharp step only one parameter (height) is required. Nenni & Gluyas (1966) first explicitly gave a critical height for sharp forward-facing steps corresponding to a Reynolds number, defined according to the step height $H$ , of $Re_{H,critical}=U_{\infty }H_{critical}/\unicode[STIX]{x1D708}=1800$ , where $H_{critical}$ correlates to the measured onset of transition such that the transition location first begins to move upstream as $H$ increases above the critical value $H_{critical}$ , and below $H_{critical}$ the transition location is generally unaffected by the presence of the step. $Re_{H,critical}$ is only a rough number without considering variation of the streamwise location or pressure gradient.

As discussed by Edelmann & Rist (2015), research on the influence of steps on the stability of the boundary layer can be divided into two approaches: one focuses on finding a critical step height $Re_{H,critical}$ (Nenni & Gluyas 1966) whereas the other is based on the idea that the effect of a protuberance can be incorporated in the $e^{N}$ method (Perraud et al. 2004; Wang & Gaster 2005; Crouch, Kosorygin & Ng 2006; Edelmann & Rist 2013, 2015). It is worth mentioning that Wu & Hogg (2006) showed that as the TS wave propagates through and is scattered by the mean-flow distortion induced by the roughness, it acquires a different amplitude downstream. They introduced the concept of a transmission coefficient. A further numerical study by Xu et al. (2016) confirms the localised isolated roughness has a local stabilising effect, but overall a destabilising effect. Additionally an alternate expression of the transmission coefficient is introduced which can be incorporated into the $e^{N}$ method.

Recently, based on the second approach, Edelmann & Rist (2015) found that generally, for transonic flows, sharp forward-facing steps led to an enhanced amplification of disturbances. They also found subsonic and supersonic results showed significant differences in the generation mechanism of the separation bubbles. A different phenomenon was found for incompressible flows when investigated numerically, by using an immersed boundary technique (Wörner, Rist & Wagner 2003). The authors observed that for a non-dimensional frequency ${\mathcal{F}}=49.34$ , the amplitude of the TS wave is reduced throughout the domain considered by the forward-facing step. They attribute this stabilising effect to the thinner boundary layer evolving on the step in comparison to the boundary layer without a step. They also claimed that when a small separation zone appears in front of the step it has no influence on the TS wave.

The presence of separation bubbles gives rise to a destabilising effect on a boundary layer. Generally, the separated shear layer will undergo rapid transition to turbulence and, even at rather small Reynolds numbers, separation provokes an increase in velocity perturbations and laminar flow breakdown, taking place in the separation region or close to it. The first observation of laminar separation bubbles was undertaken by Jones (1938) and the structure of a time-averaged bubble was given by Horton (1968); the interested reader can find a detailed review of the experimental work on the subject in Young & Horton (1966). Hammond & Redekopp (1998) found that a separation bubble could become absolutely unstable for a peak reversed flow velocity in excess of 30 % of the free-stream velocity. Theofilis (2000) subsequently reported on the shape of the globally unstable mode in recirculation bubbles. A separation bubble can have important impact on the global stability of a boundary layer. In the following, we shall only focus on amplification of the TS wave by a separation bubble. Numerically, with laminar separation bubbles, Rist (1993) suggested a 3D oblique mode breakdown rather than a secondary instability of finite-amplitude 2D waves. Xu et al. (2016) investigated the behavior of TS waves undergoing small-scale localised distortions and found even a small separation bubble can amplify a TS wave. When a sharp forward-facing step of sufficient height is present in a boundary layer, a separation bubble can easily be generated. In particular, the effective transformation or scattering of the free-stream disturbances to TS waves occurs preferably alongside sudden changes of the mean flow (e.g. over the leading edge, separation region or suction slits). The external acoustics, surface vibrations and vortical disturbances in the form of localised flow modulations or free-stream turbulence are those which most frequently contribute to the boundary layer receptivity, as reviewed by Nishioka & Morkovin (1986), Kozlov & Ryzhov (1990), Saric (1990), Bippes (1999). Additionally, a smooth step is less receptive than a sharp step (Kachanov et al. 1979a ). Another benefit of using a smooth step is to circumvent biglobal instability (Hammond & Redekopp 1998).

Figure 1. Overview of the computational setup with the Blasius boundary layer profile at the inflow and the disturbance position.

1.2 Problem definition

The smooth step considered in this paper, illustrated in figure 1, is located in the unstable regime of the neutral stability curve close to the leading edge. In the following study we consider medium-frequency and frequencies ${\mathcal{F}}\in \{100,140,150,160\}$ 2D TS waves but also investigate a low-frequency case with forcing ${\mathcal{F}}=49.34$ for comparison with Wörner et al. (2003). The low-frequency forcing is particularly interesting because it offers, in the context of the neutral stability curve of the zero-pressure-gradient flat plate, a much larger unstable regime compatible with the so-called critical amplification factor $N=8$ (Edelmann & Rist 2015). Recently, Downs & Fransson (2014) studied TS wave growth over spanwise-periodic surface patterns excited at ${\mathcal{F}}\in \{100,110,120,130\}$ . They report that TS waves excited by high frequencies and large amplitudes ( $A_{TS}^{int,I}<0.48\,\%U_{\infty }$ ), producing well-resolved profiles without triggering secondary instabilities, can be reduced by spanwise-periodic surface patterns compared to the flat plate case. Therefore, over a smooth step, understanding growth properties of the TS waves with high frequencies is also likely to be pertinent. The linear analysis shows that in the presence of a single smooth step, the TS wave can be attenuated for steps below a critical height and smoothness but amplified above this critical height. Further, the linear stability investigation of two separated smooth steps, instead of a single step, with the same geometrical configuration revealed further reduction of the amplitude of the TS wave can be obtained compared to a single smooth step. Again, past a critical height, two forward-facing smooth steps can have a destabilising effect on the 2D TS mode. Furthermore, a smooth step can tolerate a greater height scale compared with a sharp step and does not introduce separation bubbles. In order to validate the stabilising effect of the smooth forward-facing steps seen in the linear stability analysis, fully nonlinear DNS of both the K- and H-type transition scenarios are conducted. These two transition scenarios are insightful because they exhibit a long region of linear growth particularly suitable for the investigation of the effect of the forward-facing smooth step in the boundary layer on the TS wave (Sayadi, Hamman & Moin 2013). The results from the DNS confirm the findings from the linear analysis. For both K- and H-type transition scenarios the forward-facing smooth steps configuration has a stabilising effect, even avoiding transition for the K-type scenario. Further, by introducing Gaussian white noise with both fixed and random phase shifts into the DNS, robustness of the strategy is demonstrated.

The paper is organised as follows. In § 2, we give fundamental definitions and describe the numerical tools. In § 3, we present results of linear analysis for TS wave frequencies ${\mathcal{F}}\in [42,160]$ for the 2D linear stability problem. In § 4, the results from the DNS are presented and discussed for 3D nonlinear stability problem. A further discussion is then given in § 5 where the work is concluded.

2 Mathematical formulations and numerical approach

2.1 Fully nonlinear and linearised Navier–Stokes equations

The non-dimensional momentum and continuity equations governing unsteady viscous flow with constant density are given as follows

(2.1) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x2202}_{t}u_{i}-Re^{-1}\unicode[STIX]{x2202}_{j}^{2}u_{i}+u_{j}\unicode[STIX]{x2202}_{j}u_{i}+\unicode[STIX]{x2202}_{i}p=0,\\ \displaystyle \unicode[STIX]{x2202}_{j}u_{j}=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$

where $u_{i}$ is one component of the velocity field along the $i$ th direction, $\unicode[STIX]{x2202}_{t}$ denotes the derivative with respect to time, $\unicode[STIX]{x2202}_{j}$ is the derivative in the $j$ th spatial direction, $Re$ is the Reynolds number defined by $LU_{\infty }/\unicode[STIX]{x1D708}$ where $L$ is the distance from the leading edge, $\unicode[STIX]{x1D708}$ is the kinematic viscosity and $p$ is the pressure. For a 2D problem, $i=1,2$ and $(u_{1},u_{2})=(u,v)$ and for a 3D problem, $i=1,2,3$ and $(u_{1},u_{2},u_{3})=(u,v,w)$ .

Considering a steady state $\bar{u}_{i}$ of (2.1) about which a small perturbation $\tilde{u} _{i}$ , such that $u_{i}=\bar{u}_{i}+\tilde{u} _{i}$ , and dropping the second-order terms in $\tilde{u} _{i}$ , (2.1) can be linearised as follows

(2.2) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x2202}_{t}\tilde{u} _{i}-Re^{-1}\unicode[STIX]{x2202}_{j}^{2}\tilde{u} _{i}+\bar{u}_{j}\unicode[STIX]{x2202}_{j}\tilde{u} _{i}+\tilde{u} _{j}\unicode[STIX]{x2202}_{j}\bar{u}_{i}+\unicode[STIX]{x2202}_{i}\tilde{p}=0,\\ \displaystyle \unicode[STIX]{x2202}_{j}\tilde{u} _{j}=0.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

With suitable boundary conditions, in a linear regime, the system (2.2) can be used to exactly simulate evolution of a small perturbation $\tilde{u} _{i}$ in a boundary layer.

In the flat-plate simulations undertaken, with the assumptions of relatively large $Re$ and no pressure gradient, the base flow can be approximated by the well-known Blasius equation

(2.3) $$\begin{eqnarray}f^{\prime \prime \prime }(\unicode[STIX]{x1D702})+{\textstyle \frac{1}{2}}f(\unicode[STIX]{x1D702})f^{\prime \prime }(\unicode[STIX]{x1D702})=0,\end{eqnarray}$$

subject to the following boundary conditions

(2.4a,b ) $$\begin{eqnarray}f(\unicode[STIX]{x1D702})=f^{\prime }(\unicode[STIX]{x1D702})=0\quad \text{at }\unicode[STIX]{x1D702}=0,~f^{\prime }=1\quad \text{at }\unicode[STIX]{x1D702}\rightarrow \infty ,\end{eqnarray}$$

where the prime denotes the derivative with respect to the similarity variable $\unicode[STIX]{x1D702}$ . Specifically in the above, the dimensionless variables are defined by

(2.5a,b ) $$\begin{eqnarray}f=\unicode[STIX]{x1D6F9}/\sqrt{\unicode[STIX]{x1D708}U_{\infty }x}\quad \text{and}\quad \unicode[STIX]{x1D702}=y\sqrt{U_{\infty }/(\unicode[STIX]{x1D708}x)},\end{eqnarray}$$

where $\unicode[STIX]{x1D6F9}$ is the stream function. The streamwise and vertical velocity profiles of the Blasius boundary layer can be calculated by

(2.6a,b ) $$\begin{eqnarray}\bar{u}_{B}=U_{\infty }\,f^{\prime }(\unicode[STIX]{x1D702})\quad \text{and}\quad \bar{v}_{B}=\frac{1}{2}\sqrt{\frac{\unicode[STIX]{x1D708}U_{\infty }}{x}}(\unicode[STIX]{x1D702}\,f^{\prime }(\unicode[STIX]{x1D702})-f(\unicode[STIX]{x1D702})).\end{eqnarray}$$

Under the assumption of streamwise parallel flow in two dimensions, the perturbation assumes the normal form

(2.7) $$\begin{eqnarray}(\tilde{u} ,\tilde{v},\tilde{p})=(\hat{u} ,\hat{v},\hat{p})\exp (\text{i}(\unicode[STIX]{x1D6FC}x-\unicode[STIX]{x1D714}t))+\text{c.c.},\end{eqnarray}$$

where $\unicode[STIX]{x1D6FC}$ and $\unicode[STIX]{x1D714}$ denote wavenumber and frequency of a perturbation, respectively. The mode $(\hat{u} ,\hat{v},\hat{p})$ in (2.7) generally can be obtained by solving the well-known Orr–Sommerfeld (O–S) equation, the solution of which for eigenvalues and eigenfunctions has been well studied (Stuart 1963; Schlichting & Gersten 1968; Drazin & Reid 1981). When temporal stability is studied, the perturbation (2.7) can be obtained by solving the O–S equation with the imposed condition that $\unicode[STIX]{x1D6FC}$ is real, and then the complex speed $\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FC}$ is calculated; when spatial stability is studied, the condition of real frequency $\unicode[STIX]{x1D714}$ is imposed and the wavenumbers are calculated. For spatial stability, by integrating the spatial growth rate $-\text{Im}(\unicode[STIX]{x1D6FC})$ of convective perturbations, amplification of their amplitude can be obtained along the streamwise direction. When a surface imperfection occurs, the same notations $\hat{u}$ and $\hat{v}$ are used to denote the TS mode.

Generally, for numerical solutions of the linearised Navier–Stokes equations, considering spatial convective instability and a perturbation (2.7) propagating along the positive $x$ direction, the frequency is real ( $\unicode[STIX]{x1D714}\in \mathbb{R}^{+}$ ). Assuming that the TS mode is dependent on both $x$ and $y$ , the TS wave envelope is defined by the absolute maximum amplitude of the TS wave as follows

(2.8) $$\begin{eqnarray}A(x)=\max \{|\tilde{u} (x,\unicode[STIX]{x1D702},t)|:\forall \unicode[STIX]{x1D702}\in [0,\infty ),\forall t\in \mathbb{R}^{+}\}.\end{eqnarray}$$

2.2 Definitions correlated with a surface imperfection

In order to rescale the step, we introduce a reference boundary layer thickness $\unicode[STIX]{x1D6FF}_{99}=4.91x_{c}Re_{x_{c}}^{-1/2}$ and displacement thickness scales $\unicode[STIX]{x1D6FF}^{\ast }|_{x_{c}}=1.7208x_{c}Re_{x_{c}}^{-1/2}$ , defined according to a flat plate boundary layer, where $x_{c}$ is the distance from the leading edge to the centre position of a surface imperfection and $Re_{x_{c}}=U_{\infty }x_{c}/\unicode[STIX]{x1D708}$ . We also let $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=U_{\infty }\unicode[STIX]{x1D6FF}^{\ast }/\unicode[STIX]{x1D708}$ be the displacement Reynolds number. Now, we consider a forward-step-like surface imperfection, which is defined by

(2.9) $$\begin{eqnarray}f_{s}(X,{\hat{h}})=\frac{{\hat{h}}}{2}\left(1+\text{erf}\left(\frac{X}{\sqrt{2}\hat{d}}\right)\right),\end{eqnarray}$$

where $\hat{d}$ and ${\hat{h}}({>}0)$ are the streamwise width scale and the normal direction length scale defined by the corresponding physical scales $d$ and $h$ as

(2.10a,b ) $$\begin{eqnarray}{\hat{h}}=h/\unicode[STIX]{x1D6FF}_{99},\quad \hat{d}=d/\unicode[STIX]{x1D6FF}_{99},\end{eqnarray}$$

and $X$ is a streamwise local coordinate defined as follows

(2.11) $$\begin{eqnarray}X=(x-x_{c})/\unicode[STIX]{x1D6FF}_{99}.\end{eqnarray}$$

For multiple smooth steps, the wall profile is formally defined by

(2.12) $$\begin{eqnarray}\mathop{\sum }_{i=0}^{n}f_{s}(X-X_{i},{\hat{h}}),\end{eqnarray}$$

where $X_{i}$ denotes the relative position of each individual step with respect to the first step located at $X_{0}=0$ , and $n+1$ is the number of steps.

In order to characterise or quantify geometrical steepness of a continuous function $f(x)$ , assuming that $f(x)\in C^{1}$ , we introduce the following quantity

(2.13) $$\begin{eqnarray}\unicode[STIX]{x1D6FE}(x)=\frac{\max |\unicode[STIX]{x2202}_{x}\,f(x)|}{\sqrt{\max |\unicode[STIX]{x2202}_{x}\,f(x)|^{2}+\unicode[STIX]{x1D700}^{-2}}},\end{eqnarray}$$

where $\unicode[STIX]{x1D700}$ is a smooth parameter. It is clear that $\unicode[STIX]{x1D6FE}\in [0,1)$ . For a smooth step, $\unicode[STIX]{x1D700}$ is defined by the ratio ${\hat{h}}/\hat{d}=h/d\in [0,\infty )$ and the formula (2.13) can be interpreted in the following limits:

(2.14) $$\begin{eqnarray}\unicode[STIX]{x1D6FE}(X)=\left\{\begin{array}{@{}rl@{}}1, & {\hat{h}}/\hat{d}\rightarrow \infty \text{for }{\hat{h}}\neq 0\\ 0, & {\hat{h}}/\hat{d}\rightarrow 0\\ \end{array}\right.,\quad \text{for }f(X)=f_{s}(X,{\hat{h}}),X\in [-\hat{d}/2,\hat{d}/2].\end{eqnarray}$$

When $\unicode[STIX]{x1D6FE}=1$ the step is sharp, whereas for $\unicode[STIX]{x1D6FE}=0$ the smooth step tends to a flat plate. In this paper, the width scale $\hat{d}$ , which is fixed, is comparable to the TS wavelength. As indicated for an isolated roughness in Wu & Hogg (2006), this choice of $\hat{d}$ leads to a direct significant interaction between an isolated step and the TS wave. Therefore, step height ${\hat{h}}$ remains as a unique free parameter, which determines the value of $\unicode[STIX]{x1D6FE}(X)$ .

2.3 Numerical strategy

A spectral/hp element discretisation, implemented in the Nektar++ package (Cantwell et al. 2015), is used in this work to solve the linear as well as nonlinear Navier–Stokes equations. A stiffly stable splitting scheme is adopted, which decouples the velocity and pressure fields, and time integration is achieved by a second-order accurate implicit–explicit scheme (Karniadakis, Israeli & Orszag 1991).

Figure 2. Streamwise (a–c) and wall-normal (d–f) velocity profiles (around the step located at $X=0$ ) for three different streamwise locations: (a,d) $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=821$ at $X=-20.87$ , (b,e) $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=866$ at $X=0$ and (c,f) $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=897$ at $X=15.11$ . The physical parameters corresponding to each case are from case D in table 2.

For 2D simulations, a convergence study by p-type refinement is performed to demonstrate resolution independence. For 3D calculations, the same 2D mesh in the $x{-}y$ plane is used with the addition of a hybrid Fourier-Spectral/hp discretisation in the third direction, yielding a hybrid Fourier/spectral/hp discretisation of the full 3D incompressible Navier–Stokes equations.

To obtain the best fidelity in representing the curved surface of the smooth step, high-order curved elements are defined by means of an analytical mapping. The governing equations are then discretised in each curved element by seventh-order polynomials. The choice of polynomial order is guaranteed by the mesh independence study. Figure 2 compares the horizontal and vertical velocity profiles over a smooth step at different positions for polynomial order ranging from sixth to eighth. In the whole domain, the $L^{2}$ relative error of velocity fields is lower than $10^{-6}$ , which is consistent with the convergence tolerance of the base flow generation defined by

(2.15) $$\begin{eqnarray}\Vert (\unicode[STIX]{x2202}_{t}^{d}u,\unicode[STIX]{x2202}_{t}^{d}v)\Vert _{0}/\Vert (u,v)\Vert _{0}T_{c}<10^{-6},\end{eqnarray}$$

where $\Vert \cdot \Vert _{0}$ means the standard $L^{2}$ norm, $\unicode[STIX]{x2202}_{t}^{d}$ denotes the discrete temporal derivative and $T_{c}$ is the convective time scale based on the free-stream velocity and a unit length. Once 2D steady base flows are generated by using the nonlinear Navier–Stokes equations (NSEs), the TS waves are simulated by the linearised Navier–Stokes equations (LNSEs). As discussed below, for base flow generation, the inlet position is located sufficiently far from the first step to allow the base flows to recover the Blasius profile. Following the experimental methodology used by Downs & Fransson (2014), the TS waves are excited by periodic suction and blowing on the wall.

3 2D linear-stability problem

3.1 Linear analysis in a narrow unstable regime of the neutral stability curve

Figure 3. Positions of exciters $(+)$ as well as (a) the location of an isolated smooth step and (b) the location of two smooth steps in terms of the flat plate neutral stability curve. The three different excitation frequencies of the TS wave, based on the step location, are also shown by horizontal dashed lines.

As already mentioned, in order to detect the effect of smooth steps on the 2D stability of the boundary layer, three different frequency perturbations ( ${\mathcal{F}}\in \{140,150,160\}$ ) are excited within the boundary, upstream of the unstable region, by spanwise-uniform periodic blowing and suction (see figure 3). As an illustration, we show changes of the base flow for case D ( ${\hat{h}}=30\,\%$ ) in table 1 and the contour plots of $u/U_{\infty }$ , $u/U_{\infty }-\bar{u}_{B}$ , $v/U_{\infty }$ and $v/U_{\infty }-\bar{v}_{B}$ are given in figure 4. We observe that in the presence of the smooth step, the contour lines of $u/U_{\infty }$ and $v/U_{\infty }$ are altered in the following manner. The streamwise velocity decreases slightly in front of the step and increases slightly over the step, while the vertical velocity is only increased around the step. As a further comparison, we show the horizontal and vertical velocity profiles at three different positions in figure 5. Moreover, figure 6 shows that $\unicode[STIX]{x1D6FF}^{\ast }$ increases in front of the step and decreases over the step. We observe that when the TS wave propagates over a smooth step, the amplitude of the TS wave is generally amplified in front of the step and attenuated over the step. The following linear analysis is used to elucidate this phenomenon. Hereafter, for each perturbation frequency studied, let $A_{0}$ indicate a reference maximum TS mode amplitude at the lower branch of the neutral stability curve in a flat plate boundary layer. The contours of $|\tilde{u} |/A_{0}$ are given in figure 7 for three different non-dimensional frequencies ( ${\mathcal{F}}\in \{140,150,160\}$ ) and for four different single smooth steps of varying heights ${\hat{h}}=5.45\,\%,10.96\,\%,20\,\%$ and $30\,\%$ all located in $Re_{\unicode[STIX]{x1D6FF}_{\ast }^{c_{1}}}=680$ . A summary of the parameters of these computations can be found in table 1.

Table 1. Parameters for smooth steps where $Re_{\unicode[STIX]{x1D6FF}_{i}^{\ast }}$ , $Re_{\unicode[STIX]{x1D6FF}_{c_{1}}^{\ast }}$ and $Re_{\unicode[STIX]{x1D6FF}_{c_{2}}^{\ast }}$ are, respectively, the inlet Reynolds number, the Reynolds number at the centre of the first step and the Reynolds number at the centre of the second step. ${\mathcal{F}}$ denotes the non-dimensional perturbation frequency. $L_{x}$ and $L_{y}$ denote the streamwise extent and height of the domain for which the 2D base flow field obtained was independent of domain size.

Figure 4. Changes of velocity fields from the Blasius profile: (a) $u/U_{\infty }$ ; (b) $u/U_{\infty }-\bar{u}_{B}$ ; (c) $v/U_{\infty }$ ; (d) $v/U_{\infty }-\bar{v}_{B}$ for a step of height ${\hat{h}}=30\,\%$ (case D in table 1). The vertical red line represents the location of the forward-facing smooth step.

Figure 5. Comparison of base flow profiles of the boundary layers over a flat plate (dotted lines) and a smooth step (solid lines): (a) streamwise velocities $u/U_{\infty }$ and $\bar{u}_{B}$ ; (b) vertical velocities $v/U_{\infty }$ and $\bar{v}_{B}$ . The physical parameters are from case D in table 1. $u/U_{\infty }$ and $\bar{u}_{B}$ are rescaled by a factor 20. $v/U_{\infty }$ and $\bar{v}_{B}$ are rescaled by a factor 1000.

Figure 6. Displacement thickness $\unicode[STIX]{x1D6FF}^{\ast }$ rescaled by $\unicode[STIX]{x1D6FF}_{c_{1}}^{\ast }$ . The vertical grey line represents the location of the forward-facing smooth step and the arrow indicates ${\hat{h}}$ is increasing. The solid coloured lines correspond to cases A, B, C and D in table 1. The dashed dark line indicates ${\hat{h}}=0$ .

First, we observe that around the smooth step, the TS mode is energised and subsequently weakened (figure 7 a–l). By energising we mean that around the step, there exists a local maximum of $|\tilde{u} |/A_{0}$ . Secondly, a higher step height ${\hat{h}}$ gives a stronger local maximum. Finally, increasing the height of the step moves the location of maximum amplitude of the TS mode downstream. For example, for the excitation frequency ${\mathcal{F}}=150$ the maximum is located at $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=920$ for ${\hat{h}}=5.48\,\%$ (figure 7 c) but at $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=950$ for ${\hat{h}}=30\,\%$ (figure 7 j).

Figure 7. Contour plots of $|\tilde{u} |/A_{0}$ for steps of different magnitudes and exposed to TS waves of frequencies ${\mathcal{F}}=\{140,150,160\}$ . (a,c,e) ${\hat{h}}=5.48\,\%$ , (b,d,f) ${\hat{h}}=10.96\,\%$ , (g,i,k) ${\hat{h}}=20\,\%$ and (h,j,l) ${\hat{h}}=30\,\%$ . The step position is determined by $Re_{\unicode[STIX]{x1D6FF}_{\ast }^{c_{1}}}$ . The red cross + indicates the location of the maximum amplitude of the TS-wave and the vertical grey line represents the location of the forward-facing smooth step.

The results of our linear analysis reveal behaviour distinct from the results for a sharp step ( $\unicode[STIX]{x1D6FE}=1$ ) of height $h/\unicode[STIX]{x1D6FF}^{\ast }=0.235$ ( ${\hat{h}}=8.24\,\%$ ) given by Wörner et al. (2003), where they claim that a forward-facing sharp step showed a stabilising effect without a local destablisation regime despite a separation bubble being reported in front of the step. Recently, through further numerical calculations, Edelmann & Rist (2015) observed that, for subsonic Mach numbers and larger height ( $h/\unicode[STIX]{x1D6FF}^{\ast }=0.94$ or ${\hat{h}}=33\,\%$ ), two separation bubbles, in front and on top of the step, were observed and strong amplification of the disturbances was found in front of and behind the step. The results from the linear analysis, and more generally the results from the DNS presented in § 4, underline the attractiveness of replacing a forward-facing sharp step ( $\unicode[STIX]{x1D6FE}=1$ ) with large ${\hat{h}}$ by a smooth one ( $\unicode[STIX]{x1D6FE}<1$ ) because the smooth step with the same ${\hat{h}}$ does not lead to a separation bubble. We attribute the discrepancy between the current findings and the work of Edelmann & Rist (2015) to a step-induced separation bubble that has a strong destabilising effect on the TS mode. Furthermore, for a forward-facing smooth step of fixed height, the position of the global maximum value of a contour varies with respect to the given frequency, which is consistent with the relative position of the step with respect to the position of the upper branch when changing frequency in the neutral curve diagram (figure 7(g,i,k) for example). For two isolated smooth steps, a similar phenomenon is observed in figure 8(g,i,k) except that two distinct local maxima are observed around each smooth step for large ${\hat{h}}$ . From figures 7 and 8, it can be concluded that both for single- and two-step configuration global maximum values of $|\tilde{u} |/A_{0}$ depended on the frequencies, ${\hat{h}}$ and smoothness.

Figure 8. Contour plots of $|\tilde{u} |/A_{0}$ for two equal height steps of different magnitudes and exposed to TS waves of frequencies ${\mathcal{F}}=\{140,150,160\}$ . (a,c,e) ${\hat{h}}=5.48\,\%$ , (b,d,f) ${\hat{h}}=10.96\,\%$ , (g,i,k) ${\hat{h}}=20\,\%$ and (h,j,l) ${\hat{h}}=30\,\%$ . The step positions are determined by $Re_{\unicode[STIX]{x1D6FF}_{\ast }^{c_{1}}}$ and $Re_{\unicode[STIX]{x1D6FF}_{\ast }^{c_{2}}}$ . The red cross + indicates the location of the maximum amplitude of the TS-wave and the vertical grey line represents the location of the forward-facing smooth step.

By extracting the maximum values of the envelope of the TS mode at each streamwise location, the $A/A_{0}$ profiles for both the single and double smooth steps cases are shown in figure 9. We notice that a high enough smooth step significantly locally amplifies the TS wave in the vicinity of the step. From figure 9(a,c,e), we observe that when ${\hat{h}}<20\,\%$ , the TS waves are stabilised downstream for small ${\hat{h}}$ . However when ${\hat{h}}\geqslant 20\,\%$ , the most amplified flat plate TS modes corresponds to the lowest frequency ${\mathcal{F}}=140$ . The reason for this may well lie in that, for this fixed step position, this lower frequency has a higher instability even for the flat plate cases, which are indicated by the open circles in this figure. Obviously from this figure we also observe that larger step heights have an influence on the $Re_{\unicode[STIX]{x1D6FF}^{\ast }}$ for which instability starts and the rate at which the TS waves grow in the single-step case shown in figure 9(a,c,e).

In figure 10, a comparison of the TS modes at sections before the step, in the middle of the step and after the step are shown, for ${\mathcal{F}}=150$ , to help elucidate the stabilisation effect. From this figure we observe in figure 10(a) that before the step, as ${\hat{h}}$ is increased, the profiles have a similar pattern but are amplified. However, at the centre of the step and after the step (figure 10 b,c), the profiles again retain a similar pattern to the flat plate profiles but are less amplified.

Figure 9. Relative amplitude of the TS modes $A/A_{0}$ as a function of streamwise location for each of step heights ${\hat{h}}=5.48\,\%$ , $10.96\,\%$ , $20\,\%$ and $30\,\%$ for single-step (a,c,e) and double-step (b,d,f) cases. (a,b)  ${\mathcal{F}}=140$ , (c,d)  ${\mathcal{F}}=150$ and (e,f)  ${\mathcal{F}}=160$ . The vertical grey lines represents the locations of the smooth steps.

From figure 9(a,c,e), assuming the local growth (or destabilisation) of the TS wave does not trigger any nonlinear phenomena, a smooth step of low height is not harmful for TS waves with a slightly high frequency ( $140\leqslant {\mathcal{F}}\leqslant 160$ ). In fact, to some extent, a boundary layer can benefit from a smooth step since the net instability can be reduced. In figure 9(b,d,f) envelopes of the TS waves over two isolated smooth steps at the same frequencies are shown. The positions of the two smooth steps are provided in table 1 and schematically illustrated in figure 3(b). For the frequencies considered, the second steps still lie in the unstable regime of the flat plate neutral stability curve. We observe that, surprisingly, the second steps do not locally lead to further amplification of the TS waves when ${\hat{h}}<20\,\%$ ; in contrast, the amplitudes of the TS waves are further dampened compared to the amplitude of the TS waves over both the single-step boundary layers and a flat plate boundary. Destabilisation of the TS mode is only introduced by the larger height steps.

From the results of the linear stability analysis presented above, we deduce that stabilisation or destabilisation behaviour of smooth steps depends strongly on the smoothness of the step as well as its height. For a suitable range of parameters the influence of smooth steps on a boundary layer can certainly lead to notable stabilisation. It is interesting to note that if the step was extremely smooth, a region of favourable pressure gradient would exist over the whole domain we have considered, also leading to suppression of the 2D TS-instability. However, in our study we obviously investigated the influence of a localised favourable pressure gradient introduced by a smooth forward-facing step of length scale comparable to the TS wavelength, which potentially has more practical applications.

Figure 10. Comparison of the $\tilde{u}$ (a–c) and $\tilde{v}$ (d–f) profiles of the TS modes at different location over a single smooth step at ${\mathcal{F}}=150$ . (a,d) $Re_{\unicode[STIX]{x1D6FF}}^{\ast }=680$ ; (b,e)  $Re_{\unicode[STIX]{x1D6FF}}^{\ast }=750$ and (c,f) $Re_{\unicode[STIX]{x1D6FF}}^{\ast }=800$ . $\tilde{u}$ and $\tilde{v}$ are, receptively, normalised by $\max (\tilde{u} _{f})$ and $\max (\tilde{v}_{f})$ from the corresponding flat plate boundary.

Figure 11. Comparison of the normalised amplitude of the perturbation for steps at different locations. The parameters for (a–d) are provided in table 2. The red dotted line denotes a single step at $Re_{\unicode[STIX]{x1D6FF}_{c}^{\ast }}=866$ whose location is indicated by the left vertical line; the blue solid line denotes a single step at $Re_{\unicode[STIX]{x1D6FF}_{c^{\prime }}^{\ast }}=988$ whose location is indicated by the right vertical line.

3.2 Linear analysis of smooth steps at a lower excitation frequency of ${\mathcal{F}}=100$

In the previous section, investigations of the effect of a smooth forward-facing step on the 2D stability of a boundary layer focused on the frequencies ${\mathcal{F}}\in \{140,150,160\}$ . The flat plate unstable regions corresponding to these frequencies are relatively narrow compared with lower frequencies (see figure 3). For example, for ${\mathcal{F}}=160$ the unstable region of the TS-mode on the flat plate ranges from $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=580$ to $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=830$ , whereas for a perturbation frequency of ${\mathcal{F}}=100$ the unstable region ranges from $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=700$ to $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=1100$ . We therefore will now consider an incoming TS wave with a frequency ${\mathcal{F}}=100$ in a boundary layer over a single smooth step for the cases with the parameters given in table 2. Physically, the step sizes at $Re_{\unicode[STIX]{x1D6FF}_{\ast }^{c^{\prime }}}$ are kept the same as those at $Re_{\unicode[STIX]{x1D6FF}_{\ast }^{c}}$ ; however, we are now interested in assessing the effect of the position of the step on the excitation of the TS mode. Figure 11 provides the comparison of the TS envelopes for different height steps for an isolated step in two different locations. Clearly, figure 11(a) demonstrates again that small ${\hat{h}}$ (i.e.  ${<}5\,\%$ ) does not induce significant destabilisation. However, as ${\hat{h}}$ is increased, as seen in figure 11(b–d), a destabilisation effect emerges and larger ${\hat{h}}$ gives rise to larger global maximum amplitude of the TS wave. Meanwhile, figure 11(c,d) indicates that moving the location of the smooth step downstream (yet not close to the neutral curve of the upper branch) induces a slightly stronger maximum amplification than for the more upstream location.

Figure 12. Comparison of the normalised amplitude of the perturbation for a low frequency TS wave at ${\mathcal{F}}=100$ : (a) one single step at $Re_{\unicode[STIX]{x1D6FF}_{\ast }^{c_{1}}}$ ; (b) two steps at $Re_{\unicode[STIX]{x1D6FF}_{\ast }^{c_{1}}}$ and $Re_{\unicode[STIX]{x1D6FF}_{\ast }^{c_{2}}}$ . The vertical grey lines represents the locations of the forward-facing smooth steps. Physical parameters are provided in table 3.

Table 2. Parameters for smooth steps: $Re_{\unicode[STIX]{x1D6FF}_{i}^{\ast }}$ is the inlet Reynolds number, $Re_{\unicode[STIX]{x1D6FF}_{c}^{\ast }}$ and $Re_{\unicode[STIX]{x1D6FF}_{c^{\prime }}^{\ast }}$ indicate two different locations of a step of the same physical dimension. ${\mathcal{F}}$ denotes the non-dimensional perturbation frequency.

This means that for a low-frequency TS wave, the smooth step can certainly have a destabilising role on the TS wave downstream of the step. As already mentioned when considering this type of lower-frequency TS wave, the spatial extent of the unstable regime of the neutral stability curve is larger compared to that of a higher-frequency wave. The localised stabilisation effect of the smooth step is then unable to generate a sufficiently large stabilising downstream influence such that an amplification effect is eventually induced. Furthermore, the maximum values of the TS waves’ envelopes for the upstream case are less than those for the downstream ones. This may well be expected since the TS wave has a low spatial growth rate when the wave is close to the lower branch of the neutral stability curve. In contrast, when the TS wave propagates towards the centre region of the unstable regime of the neutral stability curve, it has a larger spatial growth rate. In this study, the upstream step, located at $Re_{\unicode[STIX]{x1D6FF}_{c}^{\ast }}$ , is closer to the lower branch of the neutral stability curve compared with the step located at $Re_{\unicode[STIX]{x1D6FF}_{c^{\prime }}^{\ast }}$ , which is nearly at the central position of the unstable regime of the neutral stability curve. Therefore, the destabilisation effect in front of the step at $Re_{\unicode[STIX]{x1D6FF}_{c^{\prime }}^{\ast }}$ is to be expected to be greater than that in front of the step at $Re_{\unicode[STIX]{x1D6FF}_{c}^{\ast }}$ . This is consistent with what we observe in the TS waves’ envelopes of figure 11.

This destabilisation phenomenon is further illustrated in figure 12 for the parameters defined in table 3, where we use the same non-dimensional value of ${\hat{h}}$ as in table 2. When ${\hat{h}}=5\,\%$ and $10\,\%$ , once a second smooth step is introduced downstream, some stablisation relative to the flat plate conditions is observed, as shown in figure 12(b).

Table 3. Comparison of the normalised amplitude of the perturbation with parameters for smooth steps where $Re_{\unicode[STIX]{x1D6FF}_{i}^{\ast }}$ , $Re_{\unicode[STIX]{x1D6FF}_{c_{1}}^{\ast }}$ and $Re_{\unicode[STIX]{x1D6FF}_{c_{2}}^{\ast }}$ are, respectively, the inlet Reynolds number, the Reynolds number at the centre of the first step and the Reynolds number at the centre of the second step. ${\mathcal{F}}$ denotes the non-dimensional perturbation frequency.

The correlation between the position of the step and the TS mode amplification acts as a guideline for choosing the ideal location of a smooth step. For large ${\hat{h}}$ , the effect of a step located in a larger growth rate region clearly gives rise to a larger amplification of the TS wave. However, it is worth noting that when the height is reduced to less than $10\,\%$ , there no longer exists a strong destabilisation effect from a single smooth step, independent of the position within the unstable region which we have explored.

3.3 Ability of smooth steps to amplify the very low-frequency TS waves at ${\mathcal{F}}=42$

The studies by Wörner et al. (2003) and Edelmann & Rist (2015) considered the effect of low-frequency TS modes for a long range from the leading edge of the flat plate with $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=2200$ . In Edelmann & Rist (2015), the $N$ -factor, defined as $N=\ln (A/A_{0})$ , got close to the transition criterion of $N=8$ .

To further assess the effect of a forward-facing smooth step on a similar problem we consider a TS wave with ${\mathcal{F}}=42$ . In addition, we consider an upstream problem where the TS wave has been amplified by a recirculation bubble inside an indentation, located at $Re_{\unicode[STIX]{x1D6FF}_{r}^{\ast }}=1519$ , far upstream of the transition location where $N=8$ . We then introduce a smooth forward-facing step downstream of the indentation in the unstable region of the TS mode. The indentation is defined by

(3.1) $$\begin{eqnarray}f_{r}=\left\{\begin{array}{@{}ll@{}}-{\hat{h}}_{r}\cos (\unicode[STIX]{x03C0}X^{r}/\hat{\unicode[STIX]{x1D706}})^{3},\quad & X^{r}\in [-\hat{\unicode[STIX]{x1D706}}/2,\hat{\unicode[STIX]{x1D706}}/2],\\ 0,\quad & X^{r}\notin [-\hat{\unicode[STIX]{x1D706}}/2,\hat{\unicode[STIX]{x1D706}}/2],\end{array}\right.\end{eqnarray}$$

where $X^{r}=x-x_{c}^{r}/\unicode[STIX]{x1D6FF}_{99}^{r}$ . The parameters of this computation are given in table 4. Note that the width scale $\hat{\unicode[STIX]{x1D706}}$ is comparable with the corresponding TS wavelength. A separation bubble is induced in the indentation region, and when a base flow undergoes this distortion, the TS wave is strongly amplified. In figure 13(a), we observe that the TS waves are strongly amplified around the indentation and the $N$ -factor in the computational domain reaches $N=8$ . Downstream of the roughness, for $Re_{\unicode[STIX]{x1D6FF}_{\ast }}>1800$ , the smooth forward-facing step only has weak, local, stabilising or destabilising effect for all four cases (see figure 13 b).

In contrast, a strong destabilisation of the TS wave by the sharp step ( $\unicode[STIX]{x1D6FE}=1$ ) for low frequency is reported by Edelmann & Rist (2015), where the separation bubble induces a strong increase in $N$ -factor from $N=4$ to $N=6$ because of the existence of separation bubbles in front of the step. This contrasts with the weak destabilisation influence of a smooth step on the TS wave in a boundary layer, where negligible variation of the $N$ -factor can be seen in figure 13 even for a large ${\hat{h}}>20\,\%$ step height.

Figure 13. Effect of a smooth step for the TS wave with a very low frequency of ${\mathcal{F}}=42$ . $N=\ln (A/A_{0})$ . The indentation is located at the first vertical line and the smooth step is located at the second vertical line. (a) Overview of the TS waves’ envelopes. (b) Local view of the TS waves’ envelopes around the smooth steps. The full parameters are given in table 4.

Table 4. Parameters for a wall with an indentation and a smooth step. $Re_{\unicode[STIX]{x1D6FF}_{i}^{\ast }}$ , $Re_{\unicode[STIX]{x1D6FF}_{r}^{\ast }}$ and $Re_{\unicode[STIX]{x1D6FF}^{\ast }}$ are, respectively, the inlet Reynolds number, the Reynolds number at the centre of the indentation and the Reynolds number at the centre of the smooth step. ${\mathcal{F}}$ denotes the non-dimensional perturbation frequency. ${\hat{h}}_{r}$ and $\hat{\unicode[STIX]{x1D706}}$ are used to define the indentation (3.1), which are normalised by the boundary layer thickness at the centre position of the roughness.

4 3D nonlinear-stability problem

4.1 DNS investigation of the effect on K- and H-type transition of two forward-facing smooth steps excited by a TS wave with a frequency ${\mathcal{F}}=150$

Secondary instabilities and transition to fully developed flow is highly three-dimensional. To this end, further investigation of the influence of smooth steps on two transition scenarios is achieved with a hybrid Fourier-spectral/hp discretisation to solve 3D incompressible Navier–Stokes equations. The spanwise direction was assumed to be periodic and discretised by 80 Fourier modes and the streamwise and wall normal plane was discretized using 5576 elements (quad and triangle) within which a polynomial expansion of degree 7 is imposed. K- and H-type transitions are simulated for the flow over a flat plate and with smooth steps. A Blasius profile is imposed at the inflow and, for both scenarios, a wall-normal velocity along the disturbance strip is prescribed by the blowing and suction boundary condition (Huai, Joslin & Piomelli 1997),

(4.1) $$\begin{eqnarray}v(x,z,t)=Af(x)\sin (\unicode[STIX]{x1D714}_{A}t)+Bf(x)g(z)\sin (\unicode[STIX]{x1D714}_{B}t+\unicode[STIX]{x1D711}),\end{eqnarray}$$

where $\unicode[STIX]{x1D714}_{A}$ and $\unicode[STIX]{x1D714}_{B}$ are the frequencies of the 2D TS waves and the oblique waves, respectively. $A$ and $B$ are the disturbance amplitudes of the fundamental and the oblique waves. We denote by $\unicode[STIX]{x1D711}$ the phase shift between two modes. As considered by Huai et al. (1997) and Sayadi et al. (2013), we consider the simplest case in the present study, with $\unicode[STIX]{x1D711}$ equal to 0. As indicated by Sayadi et al. (2013), the above function models the effect of vibrating ribbon-induced disturbances. The function $f(x)$ is defined by Fasel & Konzelmann (1990)

(4.2) $$\begin{eqnarray}f(x)=15.1875\unicode[STIX]{x1D709}^{5}-35.4375\unicode[STIX]{x1D709}^{4}+20.25\unicode[STIX]{x1D709}^{3},\end{eqnarray}$$

with the parameter $\unicode[STIX]{x1D709}$

(4.3) $$\begin{eqnarray}\unicode[STIX]{x1D709}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{x-x_{1}}{x_{m}-x_{1}}\quad & \text{for}~x_{1}\leqslant x\leqslant x_{m}\\ \displaystyle \frac{x_{2}-x}{x_{2}-x_{m}}\quad & \text{for}~x_{m}\leqslant x\leqslant x_{2},\end{array}\right.\end{eqnarray}$$

where $x_{m}=(x_{1}+x_{2})/2$ and $g(z)=\cos (2\unicode[STIX]{x03C0}z/\unicode[STIX]{x1D706}_{z})$ with the spanwise wavelength $\unicode[STIX]{x1D706}_{z}$ . At $x_{1}$ and $x_{2}$ , $Re_{\unicode[STIX]{x1D6FF}_{x_{1}}^{\ast }}$ and $Re_{\unicode[STIX]{x1D6FF}_{x_{2}}^{\ast }}$ are equal to $591.37$ and $608.51$ , respectively. The distribution $f(x)$ can produce clean localised vorticity disturbances and have negligible time-dependent changes of the mean flow (Fasel & Konzelmann 1990). For the K-type transition, the oblique waves have the same frequency as the 2D wave ( $\unicode[STIX]{x1D714}_{A}=\unicode[STIX]{x1D714}_{B}$ ). Also, for the H-type transition, the oblique waves are sub-harmonic ( $\unicode[STIX]{x1D714}_{B}=\unicode[STIX]{x1D714}_{A}/2$ ). All parameters used in the investigation are given in table 5. Note that the frequencies used for the perturbation are consistent with the parameters used for the linear analysis in table 1. The schematic of the computational domain is illustrated in figure 14.

Table 5. Parameters used for the DNS simulations. ${\mathcal{F}}_{A}$ and ${\mathcal{F}}_{B}$ denote non-dimensional perturbation frequencies of the disturbance strip. $A/U_{\infty }$ and $B/U_{\infty }$ are the relative amplitudes of the disturbance amplitudes of the fundamental and oblique waves, respectively. The spanwise $L_{z}$ extent of the domain is expressed as a function of the boundary layer thickness $\unicode[STIX]{x1D6FF}_{99}$ . $T$ is the finial non-dimensional time length scale which we simulate, which is defined by $T=tU_{\infty }/L$ . $\unicode[STIX]{x1D706}_{z}$ is non-dimensionalised by the inlet boundary layer thickness, which almost has the same non-dimensional value as the scale used in Sayadi et al. (2013). The choice of $\unicode[STIX]{x1D706}_{z}/\unicode[STIX]{x1D6FF}_{99}$ is equivalent to a spanwise wavenumber of approximately 0.35 at $Re_{\unicode[STIX]{x1D6FF}_{c_{1}}^{\ast }}$ .

Figure 14. Overview of the computational setup with the Blasius boundary layer profile at the inflow, the disturbance strip and two smooth steps used for the DNS.

Figure 15. Instantaneous contours of streamwise velocity in the $xz$ -plane at height $y=0.6\unicode[STIX]{x1D6FF}_{99}^{i}$ in $Re_{\unicode[STIX]{x1D6FF}^{\ast }}\in [963,1111]$ for the K- (a) and H-type (b) transition scenarios for a flat plate ${\hat{h}}=0$ .

Figure 16. Comparison of time- and spanwise-averaged skin friction versus streamwise position $Re_{x}$ for K- (a) and H-type (b) transition scenarios for a flat plate (—) and two smooth steps of height ${\hat{h}}=5.48\,\%$ (— ⋅ —) and ${\hat{h}}=12.79\,\%$ (– –). The skin-friction profile of the Blasius boundary layer (●) is given for reference.

4.2 Effect of smooth forward-facing steps on K- and H-type transitions

The validation of the DNS results for both K- and H-type transitions is corroborated by recovering the aligned arrangement of the $\unicode[STIX]{x1D6EC}$ vortices for the K-type transition (see figure 15 a) and the staggered arrangement for the H-type transition (see figure 15 b), as experimentally observed by Berlin, Wiegel & Henningson (1999) for the flat plate boundary layer. Figure 16 shows the evolution of the skin-friction coefficient versus $Re_{\unicode[STIX]{x1D6FF}^{\ast }}$ for two different normalized height scales. We observe that, for a flat plate boundary layer, the skin friction coefficient diverges from that of the Blasius boundary layer where $\unicode[STIX]{x1D6EC}$ vortices are clearly observed, as illustrated in figure 15. In fact, $\unicode[STIX]{x1D6EC}$ vortices appear further upstream, but here we only show the $\unicode[STIX]{x1D6EC}$ vortices from the location where the skin friction coefficient diverges. The streamwise evolution of the skin-friction (see figure 16) shows the K-type transition is fully inhibited by the two smooth steps, whereas the H-type transition is delayed. Additionally, increasing the height ${\hat{h}}$ ( ${<}20\,\%$ ) further reduces the skin friction coefficient $C_{f}$ in both scenarios. The observation of these phenomena supports the result of linear analysis.

Figure 17. Comparison of the energy in modes (0,1) in blue and (0,2) in black versus streamwise position $Re_{\unicode[STIX]{x1D6FF}^{\ast }}$ over a flat plate (–) and two smooth steps with height ${\hat{h}}=5.48\,\%$ (– –) and ${\hat{h}}=12.79\,\%$ (— ⋅ —) for the K- (a) and H-type (b) transition scenarios.

To gain further insight into the different impacts on the two transition scenarios of the two forward-facing smooth steps we consider the energy growth of the main modes. We label these modes using the notation $(\unicode[STIX]{x1D714},\unicode[STIX]{x1D6FD})$ (Berlin et al. 1999), where $\unicode[STIX]{x1D714}$ and $\unicode[STIX]{x1D6FD}$ are, respectively, the frequency and spanwise wavenumber, each normalized by the corresponding fundamental frequency/wavenumber. It has been observed that the K-type transition scenario has its main initial energy in the $(1,0)$ mode. The $(1,\pm 1)$ mode also generates the $(0,\pm 2)$ mode with a small amplitude through nonlinear interaction (Berlin et al. 1999). At the late stage, the $(0,\pm 2)$ mode can grow to an amplitude comparable to that of the $(0,\pm 1)$ mode. Laurien & Kleiser (1989) and Berlin et al. (1999) have shown that the initial condition for the H-type transition has its main energy in the $(1,0)$ mode with a small amount in the oblique subharmonic $(1/2,\pm 1)$ mode. The important mode is the vortex-streak $(0,\pm 2)$ mode, which is nonlinearly generated by the subharmonic mode and vital in the transition process. As illustrated in figure 17, the $(0,2)$ mode plays a significant role in the late stages of transition for both transition scenarios with the two smooth steps. For the K-type scenario, in the transition regime, the energy of mode $(0,2)$ grows and exceeds the energy of mode $(0,1)$ . For the flat plate, the energy of mode (0,1) finally grows again until turbulence occurs. The energy of mode $(0,2)$ with the two smooth steps is less than that of mode $(0,2)$ for the flat-plate, and increasing the normalised smooth step height ${\hat{h}}$ yields stronger reduction of the energy. A similar reduction in energy is also observed for mode (0,1). Furthermore, the energy of mode (0,2) exceeds that of mode (0,1) in $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=1080$ for ${\hat{h}}=5.48\,\%$ to $Re_{\unicode[STIX]{x1D6FF}^{\ast }}=1100$ for ${\hat{h}}=12.79\,\%$ (figure 17 a) and from these points onwards the energy of mode (0,1) decays. Based on the results presented in figure 17(a), we observe that the spanwise modulation induced by mode (0,1) with energy decaying on the smooth steps leads to stabilisation of the boundary layer.

In the above, we did not consider the influence of the smooth steps and other parameters (e.g. $\unicode[STIX]{x1D711}$ ) on other modes at the weakly nonlinear stages of transition. Experimentally, Kachanov & Levchenko (1984) and Borodulin, Kachanov & Koptsev (2002) discussed the influence of the initial phase shift between the fundamental wave and the sub-harmonic pair on the resonant amplification. The phase shift has particular importance for the H-type interaction. Addressing how the smooth step influences this phase shift will be done in the next section.

Table 6. Parameters used in (4.4) and (4.5) for the DNS simulations. ${\mathcal{U}}(0,2\unicode[STIX]{x03C0})$ denotes a random number between 0 and $2\unicode[STIX]{x03C0}$ with a uniform distribution. The probability density function (PDF) of the random variable $\unicode[STIX]{x1D709}(\cdot ,t)$ is in a normal distribution ${\mathcal{N}}(\unicode[STIX]{x1D707},\unicode[STIX]{x1D70E}^{2})$ with mean $\unicode[STIX]{x1D707}$ and standard deviation $\unicode[STIX]{x1D70E}$ . The parameters defined by Groups 1 and 2 are used for (4.4) and the parameters defined by Groups 3 and 4 are used for (4.5). ‘N/A’ means ‘not applicable’.

Figure 18. Comparison of time- and spanwise-averaged skin friction versus streamwise position $Re_{x}$ for transition induced by different white noise levels at the early stage, which here indicates that the non-dimensional time $t\in [2,4]$ (a,b) (the average is implemented over two convective time scales before turbulence is fully developed) and at the fully developed stage (c,d) (the average is implemented over two convective time scales after fully developed turbulence is reached downstream) for a flat plate (—) and two smooth steps of height ${\hat{h}}=5.48\,\%$ (— ⋅ —) and ${\hat{h}}=12.79\,\%$ (– –): (a,c) the noise standard variation $\unicode[STIX]{x1D70E}=5\,\%\cdot A$ and the parameters are given by Group 1 in table 6; (b,d) the noise standard variation $\unicode[STIX]{x1D70E}=10\,\%\cdot A$ and the parameters are given by Group 2 in table 6. The skin-friction profile of the Blasius boundary layer (●) is given for reference. The disturbance is defined by $v_{\unicode[STIX]{x1D709}}(x,z,t;\unicode[STIX]{x1D709})$ in (4.4) (without phase shift).

4.3 Effect of smooth forward-facing steps on transition with white noise

In view of the possible deployment of such flow control strategies, it is pertinent to assess the effect of smooth forward-facing steps on a more general transition route than the K- and H-type transition analysed so far in this paper. To understand the transition delay effect of smooth forward-facing steps with noise akin to environmental noise, we introduce Gaussian white noise into the DNS. The white noise is introduced into the boundary conditions by a Gaussian temporal $\unicode[STIX]{x1D6FF}$ -correlated process $\{\unicode[STIX]{x1D709}(x,t)\}$ with $\mathbb{E}[\unicode[STIX]{x1D709}(\cdot ,t)]=0$ and $\mathbb{E}[\unicode[STIX]{x1D709}(\cdot ,t+\text{d}t)\unicode[STIX]{x1D709}(\cdot ,t)]=\unicode[STIX]{x1D70E}^{2}\unicode[STIX]{x1D6FF}(\text{d}t)$ , where $\unicode[STIX]{x1D70E}$ is constant. The disturbance strip expression (4.1) is replaced by the following expressions

(4.4) $$\begin{eqnarray}v_{\unicode[STIX]{x1D709}}(x,z,t;\unicode[STIX]{x1D709})=Af(x)\sin (\unicode[STIX]{x1D714}_{A}t)+\unicode[STIX]{x1D709}(x,t),\end{eqnarray}$$

or

(4.5) $$\begin{eqnarray}v_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D709}}(x,z,t;\unicode[STIX]{x1D711},\unicode[STIX]{x1D709})=Af(x)\sin (\unicode[STIX]{x1D714}_{A}t)+Bf(x)g(z)\sin (\unicode[STIX]{x1D714}_{B}t+\unicode[STIX]{x1D711}(t))+\unicode[STIX]{x1D709}(x,t),\end{eqnarray}$$

where $\unicode[STIX]{x1D711}$ is a given phase shift or a uniform random phase shift. In table 6, configurations of the parameters in (4.4) and (4.5) are given. The computational geometry, the disturbance position and the two step positions are kept the same as defined in table 5.

In figure 18(a,b), we show the skin friction profiles for two different noise levels without considering sub-harmonic disturbance before downstream fully developed turbulence is reached. We observe that in the flat plate boundary layers, transition to turbulence is much quicker than that in the boundary layers over two smooth steps. The skin friction of the flat plate boundary is greater than that of the boundary layer over two smooth steps. By considering the time scale to reach a turbulent state, two smooth steps have the ability to increase this time scale. Further, we assume that the environmental white noise is always present. In figure 18(c,d), we give the skin friction profiles calculated after fully developed downstream turbulence is reached. We notice that there still exists a transition delay effect, although the effect is not significantly strong. From figure 18, we also observe that a higher ${\hat{h}}$ (larger steepness $\unicode[STIX]{x1D6FE}(x)$ ) has a stronger delay effect and a higher noise level induces a more upstream transition position.

A phase relation between the fundamental and subharmonic modes is very important in transition. We now consider phase shift with white noise ( $\unicode[STIX]{x1D70E}=10\,\%\cdot A$ ) in the disturbance defined by (4.5). Calculations are implemented by considering two situations: (i) a fixed phase shift $\unicode[STIX]{x1D711}=\unicode[STIX]{x03C0}/4$ ; (ii) uniform random phase shift. We here only consider one height parameter ${\hat{h}}=12.79\,\%$ because of the significant computational cost of these DNS. In figure 19, the skin friction profiles are given for two settings of the phase parameter $\unicode[STIX]{x1D711}$ . Figure 19(a) shows that with a fixed phase shift and white noise, the two smooth steps configuration has a transition delay effect. When uniform random phase shift is considered, the transition delay is also observed, as shown in figure 19(b). Moreover, by comparing the skin friction profiles in figure 19(a,b), we notice that the skin friction profiles with a fixed phase $\unicode[STIX]{x1D711}=\unicode[STIX]{x03C0}/4$ diverge from that of the Blasius boundary layer earlier than those with a random phase shift.

Figure 19. Comparison of time- and spanwise-averaged skin friction versus streamwise position $Re_{x}$ for transition induced by different white noise levels at the fully developed stage (the average is implemented over two-convective time scales after fully developed turbulence is reached downstream) for a flat plate (——) and two smooth steps with height ${\hat{h}}=12.79\,\%$ (– –): (a) the noise standard variation $\unicode[STIX]{x1D70E}=10\,\%\cdot A$ with a fixed phase shift ( $\unicode[STIX]{x1D711}=\unicode[STIX]{x03C0}/4$ ) and the parameters are given by Group 3 in table 6; (b) the noise standard variation $\unicode[STIX]{x1D70E}=10\,\%\cdot A$ with a random phase shift $\unicode[STIX]{x1D711}$ and the parameters are given by Group 4 in table 6. The skin-friction profile of the Blasius boundary layer (●) is given for reference. The disturbance is defined by $v_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D709}}(x,z,t;\unicode[STIX]{x1D711},\unicode[STIX]{x1D709})$ in (4.5).

In order to further investigate the phenomenon in figure 18(a,b) and analyse the transient property of the skin friction, the following expression is introduced

(4.6) $$\begin{eqnarray}{\mathcal{C}}_{f}(x,t)=\frac{\unicode[STIX]{x1D714}}{2\unicode[STIX]{x03C0}}\int _{s\in I_{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}}(t)}C_{f}(x,s)\,\text{d}s,\end{eqnarray}$$

where $\unicode[STIX]{x1D714}$ is the typical frequency in (4.4) or (4.5) and $C_{f}(x,s)$ represents transient spanwise-averaged skin friction at the time $s$ . $I_{\unicode[STIX]{x1D6FF}}(t)$ indicates a closed $\unicode[STIX]{x1D6FF}$ ( $=\unicode[STIX]{x03C0}/\unicode[STIX]{x1D714}$ ) neighbourhood centred at $t$ . We set $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{A}$ and $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{B}$ for the disturbances (4.4) and (4.5), respectively.

Figure 20. Comparison of transition property of spanwise-averaged skin friction ${\mathcal{C}}_{f}(x,t)$ without (a,b) and with (c,d) phase shift: (a) the flat plate boundary layer corresponding to case A of Group 2 in table 6; (b) the boundary layer with two smooth steps ( ${\hat{h}}=12.79\,\%$ ) corresponding to case C of Group 2 in table 6; (c) the flat plate boundary layer corresponding to a random phase shift given in case A of Group 4 in table 6; (d) the boundary layer with two smooth steps ( ${\hat{h}}=12.79\,\%$ ) corresponding a random phase shift given in case B of Group 4 in table 6. The noise standard variation $\unicode[STIX]{x1D70E}=10\,\%\cdot A$ for all cases (a–d). The non-dimensional time parameters $\{t_{i}\}_{i=1}^{5}$ : (a,b) $t_{1}=3.42$ , $t_{2}=3.66$ , $t_{3}=3.90$ , $t_{4}=4.14$ and $t_{5}=4.38$ ; (c,d) $t_{1}=3.60$ , $t_{2}=3.84$ , $t_{3}=4.08$ , $t_{4}=4.32$ and $t_{5}=4.56$ .

In figure 20, the ${\mathcal{C}}_{f}(x,t)$ profiles are provided for the disturbances with and without a phase shift when white noise is present. From figure 20(a,b), without phase shift, we observe that at the time $t_{1}$ , in the flat plate boundary layer, downstream turbulence is well developed and the ${\mathcal{C}}_{f}(x,t)$ profiles approach a saturated state much earlier than those profiles in the boundary layer over two smooth steps. Until the time $t_{5}$ is reached, the turbulence is not fully developed downstream in the boundary layer over two smooth steps. The ${\mathcal{C}}_{f}(x,t)$ profile almost needs one more convective time scale to reach fully developed turbulence from a laminar state, compared with the flat plate boundary transition. The similar phenomenon is observed for the disturbances with uniform random phase shift in figure 20(c,d). With two smooth steps, although a random phase shift is introduced, the transition to turbulence in the boundary layer over two smooth steps is still slower than that in the flat plate boundary layer and the transition is postponed more than one convective time scale by two smooth steps.

By considering white noise and phase shift in disturbances, we demonstrate the near-practical effect of the smooth steps on delaying laminar–turbulent transition.

5 Conclusions

In this paper we considered smooth steps of varying heights and their stabilising and destabilising role on TS waves. Linear stability analyses were conducted for $140<{\mathcal{F}}<160$ , ${\mathcal{F}}=100$ and ${\mathcal{F}}=42$ frequency forcing (where an upstream indentation was also introduced) with respect to the neutral stability curve of the flat plate boundary layer. One- and two-step configurations with different heights and smoothness were analysed. Finally, DNS of various transition situations are undertaken for frequencies $140<{\mathcal{F}}<160$ forcing cases to confirm the results from the linear analysis.

The net effect of a smooth forward-facing step on the stability of the TS mode clearly depends on height. Small height smooth steps ( ${\hat{h}}<10\,\%$ ) caused minimal amplification for TS waves of frequency ranging from ${\mathcal{F}}\in [42,160]$ . For ${\hat{h}}=5,10\,\%$ both configurations with single and two forward-facing steps lead to a stabilising effect at high frequencies ${\mathcal{F}}\in [140,160]$ of the TS-mode, which is a notable improvement when two steps were considered. Although for ${\hat{h}}\geqslant 20\,\%$ destabilisation was generally observed, when considering a smooth step $\unicode[STIX]{x1D6FE}<1$ it appears to have a weaker destabilising effect than previous papers that have reported of sharp-step configurations where $\unicode[STIX]{x1D6FE}=1$ . When considering lower frequencies ${\mathcal{F}}\in [42,100]$ we again observe that small height smooth steps ${\hat{h}}<10\,\%$ are relatively safe in the sense they do not significantly amplify the TS wave. Again this result contrasts with results reported for a sharp forward-facing step, and we attribute the large amplification of the TS wave by a sharp step to the occurrence of separation bubbles. This effect is similar to the destabilisation effect induced by separation bubbles in an indentation or behind a hump or a bump (Gao, Park & Park 2011; Park & Park 2013; Xu et al. 2016). From a global stability point of view, a smooth step, even with a relatively large height, does not lead to recirculation bubbles, meaning that global instability is unlikely to be introduced.

The results obtained by DNS, for a frequency forcing ${\mathcal{F}}=150$ , support the conclusion that smooth steps can have non-negligible and positive impact on the stability of the boundary layer. For ${\hat{h}}=5.48$ and ${\hat{h}}=12.79$ , the transition to the fully developed turbulent state is delayed for the H-type transition scenario and suppressed for the K-type scenario. Finally, even in the more general case, when Gaussian white noise with fixed and random phase shift is present, the transition is delayed by smooth steps, leading us to believe the configuration of two smooth steps presented in this paper shows great potential in delaying transition.