Article contents
Influence of lock aspect ratio upon the evolution of an axisymmetric intrusion
Published online by Cambridge University Press: 21 October 2013
Abstract
Through theory and numerical simulations in an axisymmetric geometry, we examine evolution of a symmetric intrusion released from a cylindrical lock in stratified fluid as it depends upon the ambient interface thickness, 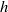 $h$ , and the lock aspect ratio
$h$ , and the lock aspect ratio 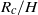 ${R}_{c} / H$ , in which
${R}_{c} / H$ , in which  ${R}_{c} $ is the lock radius and
${R}_{c} $ is the lock radius and 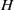 $H$ is the ambient depth. Whereas self-similarity and shallow-water theory predicts that intrusions, once established, should decelerate shortly after release from the lock, we find that the intrusions rapidly accelerate and then enter a constant-speed regime that extend between
$H$ is the ambient depth. Whereas self-similarity and shallow-water theory predicts that intrusions, once established, should decelerate shortly after release from the lock, we find that the intrusions rapidly accelerate and then enter a constant-speed regime that extend between 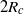 $2{R}_{c} $ and
$2{R}_{c} $ and 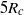 $5{R}_{c} $ from the gate, depending upon the relative interface thickness
$5{R}_{c} $ from the gate, depending upon the relative interface thickness 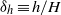 ${\delta }_{h} \equiv h/ H$ . This result is consistent with previously performed laboratory experiments. Scaling arguments predict that the distance,
${\delta }_{h} \equiv h/ H$ . This result is consistent with previously performed laboratory experiments. Scaling arguments predict that the distance, 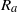 ${R}_{a} $ , over which the lock fluid first accelerates increases linearly with
${R}_{a} $ , over which the lock fluid first accelerates increases linearly with 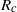 ${R}_{c} $ if
${R}_{c} $ if 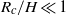 ${R}_{c} / H\ll 1$ and
${R}_{c} / H\ll 1$ and 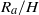 ${R}_{a} / H$ approaches a constant for high aspect ratios. Likewise in the constant-speed regime, the speed relative to the rectilinear speed,
${R}_{a} / H$ approaches a constant for high aspect ratios. Likewise in the constant-speed regime, the speed relative to the rectilinear speed, 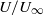 $U/ {U}_{\infty } $ , increases linearly with
$U/ {U}_{\infty } $ , increases linearly with 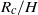 ${R}_{c} / H$ if the aspect ratio is small and is of order unity if
${R}_{c} / H$ if the aspect ratio is small and is of order unity if 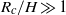 ${R}_{c} / H\gg 1$ . Beyond the constant-speed regime, the intrusion front decelerates rapidly, with power-law exponent as large as
${R}_{c} / H\gg 1$ . Beyond the constant-speed regime, the intrusion front decelerates rapidly, with power-law exponent as large as 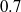 $0. 7$ if the relative ambient interface thickness,
$0. 7$ if the relative ambient interface thickness, 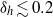 ${\delta }_{h} \lesssim 0. 2$ . For intrusions in uniformly stratified fluid (
${\delta }_{h} \lesssim 0. 2$ . For intrusions in uniformly stratified fluid ( 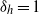 ${\delta }_{h} = 1$ ), the power-law exponent is close to
${\delta }_{h} = 1$ ), the power-law exponent is close to 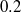 $0. 2$ . Except in special cases, the exponents differ significantly from the
$0. 2$ . Except in special cases, the exponents differ significantly from the 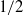 $1/ 2$ power predicted from self-similarity and the
$1/ 2$ power predicted from self-similarity and the  $1/ 3$ power predicted for intrusions from partial-depth lock releases.
$1/ 3$ power predicted for intrusions from partial-depth lock releases.
Information
- Type
- Rapids
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 2
- Cited by

