Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T07:00:22.718Z Has data issue: false hasContentIssue false
  • English
  • Français

The influence of spanwise confinement on round fountains

Published online by Cambridge University Press:  26 April 2018

Antoine L. R. Debugne Open the ORCID record for Antoine L. R. Debugne [Opens in a new window]  and
Gary R. Hunt Open the ORCID record for Gary R. Hunt [Opens in a new window]
Antoine L. R. Debugne
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
Gary R. Hunt*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email address for correspondence: gary.hunt@eng.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study experimentally the effects of spanwise confinement on turbulent miscible fountains issuing from a round source of radius 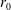$r_{0}$. A dense saline solution is ejected vertically upwards into a fresh-water environment between two parallel plates, separated by a gap of width 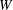$W$, which provide restraint in the spanwise direction. The resulting fountain, if sufficiently forced, rapidly attaches to the side plates as it rises and is therefore ‘confined’. We report on experiments for five confinement ratios 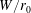$W/r_{0}$, spanning from strongly confined (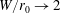$W/r_{0}\rightarrow 2$) to weakly confined (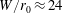$W/r_{0}\approx 24$), and for source Froude numbers 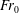$Fr_{0}$ ranging between 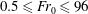$0.5\leqslant Fr_{0}\leqslant 96$. Four distinct flow regimes are observed across which the relative importance of confinement, as manifested by the formation and growth of quasi-two-dimensional structures, varies. The onset of each regime is established as a function of both 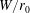$W/r_{0}$ and 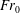$Fr_{0}$. From our analysis of the time-averaged rise heights, we introduce a ‘confined’ Froude number 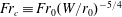$Fr_{c}\equiv Fr_{0}(W/r_{0})^{-5/4}$, which encompasses the effects of confinement and acts as the governing parameter for confined fountains. First-order statistics extracted from the flow visualisation, such as the time-averaged rise height and lateral excursions, lend further insight into the flow and support the proposed classification into regimes. For highly confined fountains, the flow becomes quasi-two-dimensional and, akin to quasi-two-dimensional jets and plumes, flaps (or meanders). The characteristic frequency of this flapping motion, identified through an ‘eddy counting’ approach, is non-dimensionalised to a Strouhal number of 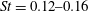$St=0.12{-}0.16$, consistent with frequencies found in quasi-two-dimensional jets and plumes.

JFM classification

Convection: Convection Convection: Plumes/thermals Wakes/Jets: Wakes/Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 845 , 25 June 2018 , pp. 263 - 292
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, W. D., Turner, J. S. & Campbell, I. H. 1990 Turbulent fountains in an open chamber. J. Fluid Mech. 212, 557–592.CrossRefGoogle Scholar
Bloomfield, L. J. & Kerr, R. C. 1998 Turbulent fountains in a stratified fluid. J. Fluid Mech. 358, 335–356.CrossRefGoogle Scholar
Burridge, H. C. & Hunt, G. R. 2012 The rise heights of low- and high-Froude-number turbulent axisymmetric fountains. J. Fluid Mech. 691, 392–416.CrossRefGoogle Scholar
Burridge, H. C. & Hunt, G. R. 2013 The rhythm of fountains: the length and time scales of rise height fluctuations at low and high Froude numbers. J. Fluid Mech. 728, 91–119.CrossRefGoogle Scholar
Burridge, H. C., Mistry, A. & Hunt, G. R. 2015 The effect of source Reynolds number on the rise height of a fountain. Phys. Fluids 27, 1–17.CrossRefGoogle Scholar
Canny, J. 1986 A computational approach to edge detection. IEEE T. Pattern Anal. PAMI‐8 (6), 679–698.CrossRefGoogle Scholar
Chen, D. & Jirka, G. H. 1998 Linear stability analysis of turbulent mixing layers and jets in shallow water layers. J. Hydraul Res. 36, 815–830.Google Scholar
Dracos, T., Giger, M. & Jirka, G. H. 1992 Plane turbulent jets in a bounded fluid layer. J. Mech. Fluids 241, 587–614.CrossRefGoogle Scholar
Friedman, P. D., Vadakoot, V. D., Meyer, W. J. & Carey, S. 2007 Instability threshold of a negatively buoyant fountain. Exp. Fluids 42, 751–759.CrossRefGoogle Scholar
Giger, M., Dracos, T. & Jirka, G. H. 1991 Entrainment and mixing in plane turbulent jets in shallow water. J. Hydraul Res. 29, 615–642.CrossRefGoogle Scholar
Hunt, G. R. & Burridge, H. C. 2015 Fountains in industry and nature. Annu. Rev. Fluid Mech. 47, 195–220.CrossRefGoogle Scholar
Hunt, G. R. & Debugne, A. L. R. 2016 Forced fountains. J. Fluid Mech. 802, 437–463.CrossRefGoogle Scholar
Jirka, G. H. 2001 Large scale flow structures and mixing processes in shallow flows. J. Hydraul Res. 39, 567–573.CrossRefGoogle Scholar
Kaye, N. B. & Hunt, G. R. 2006 Weak fountains. J. Fluid Mech. 558, 319–328.CrossRefGoogle Scholar
Landel, J. R., Caulfield, C. P. & Woods, A. W. 2012a Meandering due to large eddies and the statistically self-similar dynamics of quasi-two-dimensional jets. J. Fluid Mech. 692, 347–368.CrossRefGoogle Scholar
Landel, J. R., Caulfield, C. P. & Woods, A. W. 2012b Streamwise dispersion and mixing in quasi-two-dimensional steady turbulent jets. J. Fluid Mech. 711, 212–258.CrossRefGoogle Scholar
Mehaddi, R., Vauquelin, O. & Candelier, F. 2015 Experimental non-Boussinesq fountains. J. Fluid Mech. 784, R6.CrossRefGoogle Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Rocco, S. & Woods, A. W. 2015 Dispersion in two-dimensional turbulent buoyant plumes. J. Fluid Mech. 774, R1.CrossRefGoogle Scholar
Turner, J. S. 1966 Jets and plumes with negative or reversing buoyancy. J. Fluid Mech. 26, 779–792.CrossRefGoogle Scholar
Vinoth, B. R. & Panigrahi, P. K. 2014 Characteristics of low Reynolds number non-Boussinesq fountains from non-circular sources. Phys. Fluids 26, 1–19.CrossRefGoogle Scholar
Williamson, N., Srinarayana, N., Armfield, S. W., McBain, G. D. & Lin, W. 2008 Low-Reynolds-number fountain behaviour. J. Fluid Mech. 608, 297–317.CrossRefGoogle Scholar
Zhang, H. & Baddour, R. E. 1997 Maximum vertical penetration of plane turbulent negatively buoyant jets. J. Engng Mech. ASCE 123, 973–977.CrossRefGoogle Scholar

Debugne et al. supplementary movie 1

Weakly-confined fountains: snippet of experiment conducted at Fr0=5.4, W/r0= 4.7 (cf. figure 2).

Download Debugne et al. supplementary movie 1(Video)
Video 6.5 MB

Debugne et al. supplementary movie 2

symmetric fountains: snippet of experiment conducted at Fr0=8.9, W/r0=4.7 (cf. figure 3).

Download Debugne et al. supplementary movie 2(Video)
Video 6.1 MB

Debugne et al. supplementary movie 3

Transitional fountains: snippet of experiment conducted at Fr0=14.0, W/r0=4.7 (cf. figure 4).

Download Debugne et al. supplementary movie 3(Video)
Video 6.2 MB

Debugne et al. supplementary movie 4

Meandering fountains: snippet of experiment conducted at Fr0=24.5, W/r0=4.7 (cf. figure 5).

Download Debugne et al. supplementary movie 4(Video)
Video 6.6 MB

Debugne et al. supplementary movie 5

Illustration of the `eddy counting' approach developed in §4.3 (cf. figure 11).

Download Debugne et al. supplementary movie 5(Video)
Video 4.2 MB

Debugne et al. supplementary movie 6

Confined weak fountains: snippet of experiment conducted at Fr0=0.5, W/r0=4.7.

Download Debugne et al. supplementary movie 6(Video)
Video 2.4 MB