Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T07:35:39.723Z Has data issue: false hasContentIssue false
  • English
  • Français

The influence of the chemical composition representation according to the number of species during mixing in high-pressure turbulent flows

Published online by Cambridge University Press:  24 January 2019

Luca Sciacovelli Open the ORCID record for Luca Sciacovelli [Opens in a new window]  and
Josette Bellan Open the ORCID record for Josette Bellan [Opens in a new window]
Luca Sciacovelli
Affiliation:
California Institute of Technology, Pasadena, CA 91125, USA
Josette Bellan*
Affiliation:
California Institute of Technology, Pasadena, CA 91125, USA Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
*
†Email address for correspondence: josette.bellan@jpl.nasa.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

Mixing of several species in high-pressure (high-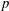$p$) turbulent flows is investigated to understand the influence of the number of species on the flow characteristics. Direct numerical simulations are conducted in the temporal mixing layer configuration at approximately the same value of the momentum ratio for all realizations. The simulations are performed with mixtures of two, three, five and seven species to address various compositions at fixed number of species, at three values of initial vorticity-thickness-based Reynolds number, 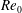$Re_{0}$, and two values of the free-stream pressure, 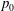$p_{0}$, which is supercritical for each species except water. The major species are C7H16, O2 and N2, and the minor species are CO, CO2, H2 and H2O. The extensive database thus obtained allows the study of the influence not only of 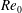$Re_{0}$ and 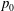$p_{0}$, but also of the initial density ratio and of the initial density difference between streams, 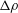$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$. The results show that the layer growth is practically insensitive to all of the above parameters; however, global vortical aspects increase with 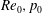$Re_{0},p_{0}$ and the number of species; nevertheless, at the same 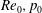$Re_{0},p_{0}$ and density ratio, vorticity aspects are not influenced by the number of species. Species mixing produces strong density gradients which increase with 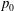$p_{0}$ and otherwise scale with 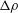$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$ but, when scaled by 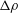$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$, are not affected by the number of species. Generalized Korteweg-type equations are developed for a multi-species mixture, and a priori estimates based on the largest density gradient show that the Korteweg stresses, which account for the influence of the density gradient, have negligible contribution in the momentum equation. The species-specific effective Schmidt number, 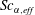$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$, is computed and it is found that negative values occur for all minor species – particularly for H2 – thus indicating uphill diffusion, while the major species experience only regular diffusion. The probability density function (p.d.f.) of 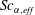$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$ shows strong variation with 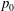$p_{0}$ but weak dependence on the number of species; however, the p.d.f. substantially varies with the identity of the species. In contrast, the p.d.f. of the effective Prandtl number indicates dependence on both 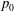$p_{0}$ and the number of species. Similar to 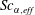$Sc_{\unicode[STIX]{x1D6FC},\mathit{eff}}$, the species-specific effective Lewis-number p.d.f. depends on the species, and for all species the mean is smaller than unity, thus invalidating one of the most popular assumptions in combustion modelling. Simplifying the mixture composition by reducing the number of minor species does not affect the crucial species–temperature relationship of the major species that, for accuracy, must be retained in combustion simulations, but this relationship is affected for the minor species and in regions of uphill diffusion, indicating that the reduction is nonlinear in nature.

JFM classification

Mathematical Foundations: General fluid mechanics Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 293 - 340
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almagro, A., Garcia-Villalba, M. & Flores, O. 2017 A numerical study of a variable-density low-speed turbulent mixing layer. J. Fluid Mech. 830, 569–601.10.1017/jfm.2017.583Google Scholar
Anderson, D. M., McFadden, G. B. & Wheeler, A. A. 1998 Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 30 (1), 139–165.10.1146/annurev.fluid.30.1.139Google Scholar
Batchelor, G. K. 1999 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bellan, J. 2017a Direct numerical simulation of a high-pressure turbulent reacting temporal mixing layer. Combust. Flame 176, 245–262.10.1016/j.combustflame.2016.09.026Google Scholar
Bellan, J. 2017b From elementary kinetics in perfectly stirred reactors to reduced kinetics utilizable in turbulent reactive flow simulations for combustion devices. Combust. Flame 184, 286–296.10.1016/j.combustflame.2017.06.013Google Scholar
Cahn, J. W. 1959 Free energy of a nonuniform system. II. Thermodynamic basis. J. Chem. Phys. 30 (5), 1121–1124.10.1063/1.1730145Google Scholar
Cahn, J. W. & Hilliard, J. E. 1958 Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28 (2), 258–267.10.1063/1.1744102Google Scholar
Chehroudi, B., Talley, D. & Coy, E. 2002 Visual characteristics and initial growth rates of round cryogenic jets at subcritical and supercritical pressures. Phys. Fluids 14 (2), 850–861.10.1063/1.1430735Google Scholar
Chung, T. H., Ajlan, M., Lee, L. L. & Starling, K. E. 1988 Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Engng Chem. Res. 27 (4), 671–679.10.1021/ie00076a024Google Scholar
Cornelisse, P. M. W.1997 The square gradient theory applied – simultaneous modelling of interfacial tension and phase behaviour. PhD thesis, Delft University.Google Scholar
Crua, C., Heikal, M. R. & Gold, M. R. 2015 Microscopic imaging of the initial stage of diesel spray formation. Fuel 157, 140–150.10.1016/j.fuel.2015.04.041Google Scholar
Crua, C., Manin, J. & Pickett, L. M. 2017 On the transcritical mixing of fuels at diesel engine conditions. Fuel 208, 535–548.10.1016/j.fuel.2017.06.091Google Scholar
Dagaut, P. & Cathonnet, M. 2006 The ignition, oxidation, and combustion of kerosene: a review of experimental and kinetic modeling. Prog. Energy Combust. Sci. 32, 48–92.10.1016/j.pecs.2005.10.003Google Scholar
Edwards, T. 2003 Liquid fuels and propellants for aerospace propulsion: 1903–2003. J. Propul. Power 19 (6), 1089–1107.10.2514/2.6946Google Scholar
Edwards, T. & Maurice, L. Q. 2001 Surrogate mixtures to represent complex aviation and rocket fuels. J. Propul. Power 17, 461–466.10.2514/2.5765Google Scholar
Edwards, T., Minus, D., Harrison, W. & Corporan, E.2004 Fischer–Tropsch jet fuels – characterization for advanced aerospace applications. AIAA Paper 2004-3885.Google Scholar
Ern, A. & Giovangigli, V. 1998 Thermal diffusion effects in hydrogen–air and methane–air flames. Combust. Theor. Model. 2, 349–372.10.1088/1364-7830/2/4/001Google Scholar
Falgout, Z., Rahm, M., Sedarsky, D. & Linne, M. 2016 Gas/fuel jet interfaces under high pressures and temperatures. Fuel 168, 14–21.10.1016/j.fuel.2015.11.061Google Scholar
Falgout, Z., Rahm, M., Wang, Z. & Linne, M. 2015 Evidence for supercritical mixing layers in the ECN Spray A. Proc. Combust. Inst. 35, 1579–1586.10.1016/j.proci.2014.06.109Google Scholar
Gaitonde, D. V. & Visbal, M. R.1998 High-order schemes for Navier–Stokes equations: algorithm and implementation into FDL3DI. Air Force Research Lab Wright-Patterson AFB OH Air Vehicles Directorate AFRL-VA-WP-TR-1998-3060.Google Scholar
Giovangigli, V., Matuszewsky, L. & Dupoirieux, F. 2011 Detailed modeling of planar transcritical H2–O2–N2 flames. Combust. Theor. Model. 15, 141–182.10.1080/13647830.2010.527016Google Scholar
Goto, S. & Kida, S. 1999 Passive scalar spectrum in isotropic turbulence: prediction by the Lagrangian direct-interaction approximation. Phys. Fluids 11 (7), 1936–1952.10.1063/1.870055Google Scholar
de Groot, S. R. & Mazur, P. 1984 Non-equilibrium Thermodynamics. Dover.Google Scholar
Hannoun, I. A., Fernando, H. J. S. & List, E. J. 1988 Turbulence structure near a sharp density interface. J. Fluid Mech. 189, 189–209.10.1017/S0022112088000965Google Scholar
Harstad, K. & Bellan, J. 2000 An all-pressure fluid drop model applied to a binary mixture: heptane in nitrogen. Intl J. Multiphase Flow 26 (10), 1675–1706.10.1016/S0301-9322(99)00108-1Google Scholar
Harstad, K. & Bellan, J. 2004a Mixing rules for multicomponent mixture mass diffusion coefficients and thermal diffusion factors. J. Chem. Phys. 120 (12), 5664–5673.10.1063/1.1650296Google Scholar
Harstad, K. & Bellan, J. 2004b High-pressure binary mass-diffusion coefficients for combustion applications. Ind. Engng Chem. Res. 43 (2), 645–654.10.1021/ie0304558Google Scholar
Harstad, K. & Bellan, J. 2013 Prediction of premixed, heptane and iso-octane jet flames using a reduced kinetic model based on constituents and species. Combust. Flame 160, 2404–2421.10.1016/j.combustflame.2013.06.005Google Scholar
Hernández, J. J., Ballesteros, R. & Sanz-Argent, J. 2010 Reduction of kinetic mechanisms for fuel oxidation through genetic algorithms. Math. Comput. Model. 52, 1185–1193.10.1016/j.mcm.2010.02.035Google Scholar
Hirshfelder, J., Curtis, C. & Bird, R. 1964 Molecular Theory of Gases and Liquids. John Wiley and Sons.Google Scholar
Jagannathan, S. & Donzis, D. A. 2016 Reynolds and Mach number scaling in solenoidally-forced compressible turbulence using high-resolution direct numerical simulations. J. Fluid Mech. 789, 669–707.10.1017/jfm.2015.754Google Scholar
Jamet, D., Lebaigue, O., Coutris, N. & Delhaye, J. M. 2001 The second gradient method for the direct numerical simulation of liquid–vapor flows with phase change. J. Comput. Phys. 169 (2), 624–651.10.1006/jcph.2000.6692Google Scholar
Keizer, J. 1987 Statistical Thermodynamics of Nonequilibrium Processes. Springer.10.1007/978-1-4612-1054-2Google Scholar
Kennedy, C. & Carpenter, M. 1994 Several new numerical methods for compressible shear layer simulations. Appl. Numer. Maths 14, 397–433.10.1016/0168-9274(94)00004-2Google Scholar
Korteweg, D. J. 1901 Sur la forme que prennent les équations du mouvements des fluides si l’on tient compte des forces capillaires causées par des variations de densité considérables mais connues et sur la théorie de la capillarité dans l’hypothèse d’une variation continue de la densité. Archives Néerlandaises des Sciences exactes et naturelles 6, 1–24.Google Scholar
Kourdis, P. D. & Bellan, J. 2014 Heavy-alkane oxidation kinetic-mechanism reduction using dominant dynamic variables, self similarity and chemistry tabulation. Combust. Flame 161, 1196–1223.10.1016/j.combustflame.2013.11.012Google Scholar
Lam, S. H. 2007 Reduced chemistry-diffusion coupling. Combust. Sci. Technol. 179, 767–786.10.1080/00102200601093498Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.10.1016/0021-9991(92)90324-RGoogle Scholar
Masi, E., Bellan, J., Harstad, K. G. & Okong’o, N. A. 2013 Multi-species turbulent mixing under supercritical-pressure conditions: modelling, direct numerical simulation and analysis revealing species spinodal decomposition. J. Fluid Mech. 721, 578–626.10.1017/jfm.2013.70Google Scholar
Mayer, W., Schik, A., Schweitzer, C. & Schaeffler, M.1996 Injection and mixing processes in high pressure LOX/GH2 rocket. AIAA Paper 96-2620.Google Scholar
Mayer, W. & Tamura, H. 1996 Propellant injection in a liquid oxygen/gaseous hydrogen rocket engine. J. Propul. Power 12, 1137–1147.10.2514/3.24154Google Scholar
Moser, R. & Rogers, M. 1991 Mixing transition and the cascade to small scales in a plane mixing layer. Phys. Fluids A 3 (5), 1128–1134.10.1063/1.858094Google Scholar
Mueller, C. J., Cannella, W. J., Bays, J. T., Bruno, T. J., DeFabio, K., Dettman, H. D., Gieleciak, R. M., Huber, M. L., Kweon, C.-B., McConnell, S. S., Pitz, W. J. & Ratcliff, M. A. 2016 Diesel surrogate fuels for engine testing and chemical-kinetic modeling: compositions and properties. Energy Fuels 30, 1445–1451.10.1021/acs.energyfuels.5b02879Google Scholar
Muller, S. M. & Scheerer, D. 1991 A method to parallelize tridiagonal solvers. Parallel Comput. 17, 181–188.10.1016/S0167-8191(05)80104-8Google Scholar
Okong’o, N. & Bellan, J. 2002 Direct numerical simulation of a transitional supercritical binary mixing layer: heptane and nitrogen. J. Fluid Mech. 464, 1–34.Google Scholar
Okong’o, N. & Bellan, J. 2004 Consistent large eddy simulation of a temporal mixing layer laden with evaporating drops. Part 1. Direct numerical simulation, formulation and a priori analysis. J. Fluid Mech. 499, 1–47.10.1017/S0022112003007018Google Scholar
Okong’o, N., Harstad, K. & Bellan, J. 2002 Direct numerical simulations of O2/H2 temporal mixing layers under supercritical conditions. AIAA J. 40 (5), 914–926.Google Scholar
Oschwald, M. & Schick, A. 1999 Supercritical nitrogen free jet investigated by spontaneous Raman scattering. Exp. Fluids 27, 497–506.10.1007/s003480050374Google Scholar
Oschwald, M., Schik, A., Klar, M. & Mayer, W.1999 Investigation of coaxial LN2/GH2-injection at supercritical pressure by spontaneous Raman scattering. AIAA Paper 99-2887.Google Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.10.1017/S0022112001006978Google Scholar
Poling, B. E., Prausnitz, J. M. & O’Connell, J. P. 2001 The Properties of Gases and Liquids, 5th edn. McGraw-Hill.Google Scholar
Rowlinson, J. S. & Widom, B. 2002 Molecular Theory of Capillarity. Dover.Google Scholar
Roy, A., Clement Joly, C. & Corin Segal, C. 2013 Disintegrating supercritical jets in a subcritical environment. J. Fluid Mech. 717, 193–202.10.1017/jfm.2012.566Google Scholar
Sandia National LaboratoriesSpray A http://www.sandia.gov/ecn/cvdata/targetCondition/sprayA.php.Google Scholar
Sarman, S. & Evans, D. J. 1992 Heat flow and mass diffusion in binary Lennard–Jones mixtures. Phys. Rev. A 45 (4), 2370–2379.10.1103/PhysRevA.45.2370Google Scholar
Seppecher, P. 1996 Moving contact lines in the Cahn–Hilliard theory. Intl J. Engng Sci. 34 (9), 977–992.10.1016/0020-7225(95)00141-7Google Scholar
Silke, E. J., Pitz, W. J. & Westbrook, C. K. 2007 Detailed chemical kinetic modeling of cyclohexane oxidation. J. Phys. Chem. A 111 (19), 3761–3775.10.1021/jp067592dGoogle Scholar
Simmie, J. M. 2003 Detailed chemical kinetic models for the combustion of hydrocarbon fuels. Prog. Energy Combust. Sci. 29, 599–634.10.1016/S0360-1285(03)00060-1Google Scholar
Taylor, R. & Krishna, R. 1993 Multicomponent Mass Transfer. John Wiley and Sons.Google Scholar
Tennekes, H. & Lumley, J. L. 1989 A First Course in Turbulence. MIT Press.Google Scholar
van der Waals, J. D. 1893 Thermodynamische theorie der capillariteit in de onderstelling van continue dichtheidsverandering. Verhand. Kon. Akad. Wetensch. Amst. (Sect. 1) 1 (8), 56 pages.Google Scholar