Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T05:46:33.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of the viscosity ratio on drop dynamics and breakup for a drop rising in an immiscible low-viscosity liquid

Published online by Cambridge University Press:  04 July 2014

Mitsuhiro Ohta ,
Yu Akama ,
Yutaka Yoshida  and
Mark Sussman
Mitsuhiro Ohta*
Affiliation:
Department of Energy System, Institute of Technology and Science, The University of Tokushima, 2-1 Minamijyousanjima-cho, Tokushima 770-8506, Japan
Yu Akama
Affiliation:
Division of Applied Sciences, Graduate School of Engineering, Muroran Institute of Technology, 27-1 Mizumoto-cho, Muroran, Hokkaido 050-8585, Japan
Yutaka Yoshida
Affiliation:
Division of Applied Sciences, Graduate School of Engineering, Muroran Institute of Technology, 27-1 Mizumoto-cho, Muroran, Hokkaido 050-8585, Japan
Mark Sussman
Affiliation:
Department of Mathematics, Florida State University, Tallahassee, FL 32306, USA
*
†Email address for correspondence: m-ohta@tokushima-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

In a low Morton number (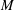$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}M$) regime, the stability of a single drop rising in an immiscible viscous liquid is experimentally and computationally examined for varying viscosity ratio 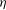$\eta $ (the viscosity of the drop divided by that of the suspending fluid) and varying Eötvös number (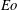$\mathit{Eo}$). Three-dimensional computations, rather than three-dimensional axisymmetric computations, are necessary since non-axisymmetric unstable drop behaviour is studied. The computations are performed using the sharp-interface coupled level-set and volume-of-fluid (CLSVOF) method in order to capture the deforming drop boundary. In the lower 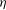$\eta $ regimes, 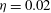$\eta = 0.02 $ or 0.1, and when 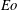$\mathit{Eo}$ exceeds a critical threshold, it is observed that a rising drop exhibits nonlinear lateral/tilting motion. In the higher 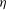$\eta $ regimes, 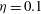$\eta = 0.1$, 1.94, 10 or 100, and when 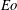$\mathit{Eo}$ exceeds another critical threshold, it is found that a rising drop becomes unstable and breaks up into multiple drops. The type of breakup, either ‘dumbbell’, ‘intermediate’ or ‘toroidal’, depends intimately on 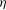$\eta $ and 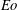$\mathit{Eo}$.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 383 - 409
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahn, H. T. & Shashkov, M. 2007 Multi-material interface reconstruction on generalized polyhedral meshes. J. Comput. Phys. 226 (2), 2096–2132.Google Scholar
Arecchi, F. T., Buah-Bassuah, P. K., Francini, F. & Residori, S. 1996 Fragmentation of a drop as it falls in a lighter miscible fluid. Phys. Rev. E 53, 424–429.Google Scholar
Arecchi, F. T., Buah-Bassuah, P. K. & Perez-Garcia, C. 1991 Fragment formation in the break-up of a drop falling in a miscible liquid. Europhys. Lett. 15, 429–434.CrossRefGoogle Scholar
Arienti, M., Li, X., Soteriou, M., Eckett, C., Sussman, M. & Jensen, B. 2013 Coupled level-set/volume-of-fluid method for simulation of injector atomization. J. Propul. Power 29 (1), 147–157.Google Scholar
Baumann, N., Joseph, D. D., Mohr, P. & Renardy, Y. 1992 Vortex rings of one fluid in another in free fall. Phys. Fluids A 4, 567–580.Google Scholar
Bhaga, D. & Weber, M. E. 1981 Bubbles in viscous liquids: shapes, wakes and velocities. J. Fluid Mech. 105, 61–85.CrossRefGoogle Scholar
Buah-Bassuah, P. K., Rojas, R., Residori, S. & Arecchi, F. T. 2005 Fragmentation instability of a liquid drop falling inside a heavier miscible fluid. Phys. Rev. E 72, 067301.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.Google Scholar
Ern, P., Risso, F., Fernandes, P. C. & Magnaudet, J. 2009 Dynamical model for the buoyancy-driven zigzag motion of oblate bodies. Phys. Rev. Lett. 102, 134505.Google Scholar
Flock, A. K., Guildenbecher, D. R., Chen, J., Sojka, P. E. & Bauer, H.-J. 2012 Experimental statistics of droplet trajectory and air flow during aerodynamic fragmentation of liquid drops. Intl J. Multiphase Flow 47, 37–49.CrossRefGoogle Scholar
Gao, J., Guildenbecher, D. R., Reu, P. L., Kulkarni, V., Sojka, P. E. & Chen, J. 2013 Quantitative, three-dimensional diagnostics of multiphase drop fragmentation via digital in-line holography. Opt. Lett. 38, 1893–1895.Google Scholar
Grace, J. R., Wairegi, T. & Brophy, J. 1978 Break-up of drops and bubbles in stagnant media. Can. J. Chem. Engng 56, 3–8.Google Scholar
Grace, J. R., Wairegi, T. & Nguyen, T. H. 1976 Shapes and velocities of single drops and bubbles moving freely through immiscible liquids. Trans. Inst. Chem. Engrs 54, 167–173.Google Scholar
Han, J. & Tryggvason, G. 1999 Secondary breakup of axisymmetric liquid drops. I. Acceleration by a constant body force. Phys. Fluids 11, 3650–3667.Google Scholar
Han, J. & Tryggvason, G. 2001 Secondary breakup of axisymmetric liquid drops. II. Impulsive acceleration. Phys. Fluids 13, 1554–1565.CrossRefGoogle Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39, 201–225.Google Scholar
Jalaal, M. & Mehravaran, K. 2012 Fragmentation of falling liquid droplets in bag breakup mode. Intl J. Multiphase Flow 47, 115–132.CrossRefGoogle Scholar
Kang, M., Fedkiw, R. & Liu, X.-D. 2000 A boundary condition capturing method for multiphase incompressible flow. J. Sci. Comput. 15, 323–360.Google Scholar
Koh, C. J. & Leal, L. G. 1989 The stability of drop shapes for translation at zero Reynolds number through a quiescent fluid. Phys. Fluids A 1, 1309–1313.CrossRefGoogle Scholar
Koh, C. J. & Leal, L. G. 1990 An experimental investigation on the stability of viscous drops translating through a quiescent fluid. Phys. Fluids A 2, 2103–2109.Google Scholar
Kojima, M., Hinch, E. J. & Acrivos, A. 1984 The formation and expansion of a toroidal drop moving in a viscous fluid. Phys. Fluids 27, 19–32.Google Scholar
Ohta, M., Akama, Y., Yoshida, Y. & Sussman, M. 2009 Three-dimensional simulations of vortex ring formation from falling drops in an immiscible viscous liquid. J. Chem. Engng Japan 42, 648–655.Google Scholar
Ohta, M., Kikuchi, D., Yoshida, Y. & Sussman, M. 2011 Robust numerical analysis of the dynamic bubble formation process in a viscous liquid. Intl J. Multiphase Flow 37, 1059–1071.Google Scholar
Ohta, M. & Sussman, M. 2012 The buoyancy-driven motion of a single skirted bubble or drop rising through a viscous liquid. Phys. Fluids 24, 112101.CrossRefGoogle Scholar
Ohta, M., Yamaguchi, S., Yoshida, Y. & Sussman, M. 2010 The sensitivity of drop motion due to the density and viscosity ratio. Phys. Fluids 22, 072102.Google Scholar
Olgac, U., Kayaalp, A. D. & Muradoglu, M. 2006 Buoyancy-driven motion and breakup of viscous drops in constricted capillaries. Intl J. Multiphase Flow 32, 1055–1071.CrossRefGoogle Scholar
Residori, S., Pampaloni, E., Buah-Bassuah, P. K. & Arecchi, F. T. 2000 Surface tension effects in the zero gravity inflow of a drop into a fluid. Eur. Phys. J. B 15, 331–334.Google Scholar
Shew, W. L. & Pinton, J.-F. 2006 Dynamical model of bubble path instability. Phys. Rev. Lett. 97, 144508.Google Scholar
Shew, W. L., Poncet, S. & Pinton, J.-F. 2006 Force measurements on rising bubbles. J. Fluid Mech. 569, 51–60.Google Scholar
Sreekantan, V.2002 Computational investigation of path instabilities in rising air bubbles. PhD Dissertation. The University of Texas at Austin.Google Scholar
Stewart, P. A., Lay, N., Sussman, M. & Ohta, M. 2008 An improved sharp interface method for viscoelastic and viscous two-phase flows. J. Sci. Comput. 35, 43–61.Google Scholar
Sussman, M. 2003 A second order coupled levelset and volume of fluid method for computing growth and collapse of vapor bubbles. J. Comput. Phys. 187, 110–136.Google Scholar
Sussman, M. 2005 A parallelized, adaptive algorithm for multiphase flows in general geometries. Comput. Struct. 83, 435–444.Google Scholar
Sussman, M., Almgren, A., Bell, J., Colella, P., Howell, L. & Welcome, M. 1999 An adaptive level set approach for incompressible two-phase flows. J. Comput. Phys. 148, 81–124.CrossRefGoogle Scholar
Sussman, M. & Puckett, E. G. 2000 A coupled level set and volume of fluid method for computing 3D and axisymmetric incompressible two-phase flows. J. Comput. Phys. 162, 301–337.CrossRefGoogle Scholar
Sussman, M., Smereka, P. & Osher, S. J. 1994 A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 114, 146–159.CrossRefGoogle Scholar
Sussman, M., Smith, K. M., Hussaini, M. Y., Ohta, M. & Zhi-Wei, R. 2007 A sharp interface method for incompressible two-phase flows. J. Comput. Phys. 221, 469–505.Google Scholar
Tomiyama, A., Celata, G. P., Hosokawa, S. & Yoshida, S. 2002 Terminal velocity of single bubbles in surface tension force dominant regime. Intl J. Multiphase Flow 28, 1497–1519.Google Scholar
Veldhuis, C. H. J., Biesheuvel, A. & Lohse, D. 2009 Freely rising light solid spheres. Intl J. Multiphase Flow 35, 312–322.Google Scholar
Wairegi, T. & Grace, J. R. 1976 The behavior of large drops in immiscible liquids. Intl J. Multiphase Flow 3, 67–77.Google Scholar
Wegener, M., Kraume, M. & Paschedag, A. R. 2010 Terminal and transient drop rise velocity of single toluene droplets in water. AIChE J. 56, 2–10.Google Scholar
Wu, M. & Gharib, M. 2002 Experimental studies on the shape and path of small air bubbles rising in clean water. Phys. Fluids 14, L49–L52.Google Scholar
Zhang, Q. & Liu, P. L.-F. 2008 A new interface tracking method: The polygonal area mapping method. J. Comput. Phys. 227, 4063–4088.Google Scholar