Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Benitez, Elizabeth K.
Borg, Matthew P.
McDaniel, Zachary A.
and
Jewell, Joseph S.
2023.
Instability and Transition Onset Downstream of an Axisymmetric Separation Bubble with Sharp and Blunt Nosetips.
Benitez, Elizabeth K.
Borg, Matthew P.
Paredes, Pedro
Schneider, Steven P.
and
Jewell, Joseph S.
2023.
Measurements of an axisymmetric hypersonic shear-layer instability on a cone-cylinder-flare in quiet flow.
Physical Review Fluids,
Vol. 8,
Issue. 8,
Nicotra, Emma
Moy, Chandler J.
Ritchie, David
Zhou, Terry
Bane, Sally P.
and
Jewell, Joseph S.
2024.
Plasma Perturbations on an Oberkampf Geometry in Quiet Mach 6 Flow.
Cao, Shibin
Hao, Jiaao
and
Guo, Peixu
2024.
Transition to turbulence in hypersonic flow over a compression ramp due to upstream forcing.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Benitez, Elizabeth K.
Borg, Matthew P.
and
Hill, J. Luke
2024.
Nosetip bluntness effects on a cone-cylinder-flare at mach 6.
Experiments in Fluids,
Vol. 65,
Issue. 5,
McDaniel, Zachary A.
and
Jewell, Joseph S.
2024.
Application of Schlieren Methods to Flared Cone in Mach-6 Quiet Tunnel.
Karpuzcu, Irmak Taylan
Levin, Deborah A
and
Theofilis, Vassilios
2024.
Effect of the Scaled Angle on the Stability of a Large Separation Bubble.
Ghannadian, Arman C.
Gosse, Ryan C.
Roy, Subrata
Lawless, Zachary
and
Jewell, Joseph S.
2024.
A Comparison of Modal Decomposition Methods Applied to Hypersonic Schlieren Video.
Benitez, Elizabeth K.
Borg, Matthew P.
Esquieu, Sébastien
Caillaud, Clément
Lugrin, Mathieu
McDaniel, Zachary A.
Jewell, Joseph S.
Scholten, Anton
Paredes, Pedro
Li, Fei
and
Choudhari, Meelan M.
2024.
Separation and Transition on a Cone-Cylinder-Flare: Experimental Campaigns.
Francis, Adelbert A.
and
Jewell, Joseph S.
2024.
Effect of Angle of Attack on Separation Bubble Instability and Transition on a Cone-Slice-Ramp in Mach-6 Quiet Flow.
Lawless, Zachary
Nicotra, Emma
and
Jewell, Joseph S.
2024.
Base Flow Measurements of a Slender Cone at Mach 6.
Francis, Adelbert A.
Dylewicz, Kamil
Klothakis, Angelos
Theofilis, Vassilios
and
Jewell, Joseph S.
2024.
Instability Measurements on a Cone-Slice-Flap in Mach-6 Quiet Flow.
Zhao, Guoqin
Ma, Tianju
Chen, Zongnan
Zhang, Zijian
Hao, Jiaao
and
Wen, Chih-Yung
2024.
Investigation of streamwise streak characteristics over a compression ramp at Mach 4.
Physics of Fluids,
Vol. 36,
Issue. 10,
Benitez, Elizabeth K.
Borg, Matthew P.
Dungan, Sean
Brehm, Christoph
and
Jewell, Joseph S.
2024.
Focused Laser Differential Interferometry Performance Over an Axisymmetric Model.
Pandey, Anshuman
Casper, Katya M.
and
Beresh, Steven J.
2024.
Relaminarization effects in hypersonic flow on a three-dimensional expansion–compression geometry.
Journal of Fluid Mechanics,
Vol. 985,
Issue. ,
Caillaud, Clément
Esquieu, Sébastien
Scholten, Anton
Paredes, Pedro
Li, Fei
Choudhari, Meelan M.
Kuehl, Joseph
Lugrin, Mathieu
Benitez, Elizabeth K.
Borg, Matthew P.
McDaniel, Zachary A.
and
Jewell, Joseph S.
2024.
Separation and Transition on a Cone-Cylinder-Flare: Computational Investigations.
Benitez, Elizabeth K.
Caillaud, Clément
McDaniel, Zachary A.
Lugrin, Mathieu
Esquieu, Sébastien
Borg, Matthew P.
Jewell, Joseph S.
Scholten, Anton
Paredes, Pedro
Li, Fei
and
Choudhari, Meelan M.
2025.
Separation and Transition on a Cone-Cylinder-Flare: Experimental Campaigns.
AIAA Journal,
Vol. 63,
Issue. 6,
p.
2162.
Davami, Jonathan
Juliano, Thomas J.
Scholten, Anton
Paredes, Pedro
Benitez, Elizabeth K.
Running, Carson L.
Little, Nolan
Duan, Lian
Dylewicz, Kamil
Pezlar, Vojtech
Theofilis, Vassilis
Thiele, Thomas
and
Willems, Sebastian
2025.
Separation and Transition on the ROTEX-T Cone–Flare.
AIAA Journal,
Vol. 63,
Issue. 9,
p.
3939.
Caillaud, Clément
Scholten, Anton
Kuehl, Joseph
Paredes, Pedro
Lugrin, Mathieu
Esquieu, Sébastien
Li, Fei
Choudhari, Meelan M.
Benitez, Elizabeth K.
Borg, Matthew P.
McDaniel, Zachary A.
and
Jewell, Joseph S.
2025.
Separation and Transition on a Cone-Cylinder-Flare: Computational Investigations.
AIAA Journal,
Vol. 63,
Issue. 7,
p.
2615.
Huang, Changye
Cao, Shibin
Hao, Jiaao
Guo, Peixu
and
Wen, Chih-Yung
2025.
Laminar-turbulent transition in a hypersonic compression ramp flow.
Physics of Fluids,
Vol. 37,
Issue. 3,
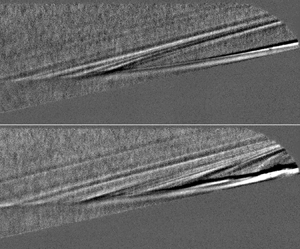
 $12^{\circ }$ flare angle under hypersonic quiet flow. Two distinct instabilities were identified: Mack's second mode (which peaked between 190 and 290 kHz) and the shear-layer instability in the same frequency band as Mack's first mode (observed between 50 and 150 kHz). Both instabilities were measured with surface pressure sensors and were captured with high-speed schlieren. Linear stability analysis results agreed well with these measured instabilities in terms of both peak frequencies and amplification rates. Lower-frequency fluctuations were also noted in the schlieren data. Bicoherence analysis revealed nonlinear phase-locking between the shear-layer and second-mode instabilities. For the first time in axisymmetric, low-disturbance flow, naturally generated intermittent turbulent spots were observed in the reattached boundary layer. These spots appeared to evolve from shear-layer-instability wave packets convecting downstream. This work presents novel experimental evidence of the hypersonic shear-layer instability contributing directly to transition onset for an axisymmetric model.
$12^{\circ }$ flare angle under hypersonic quiet flow. Two distinct instabilities were identified: Mack's second mode (which peaked between 190 and 290 kHz) and the shear-layer instability in the same frequency band as Mack's first mode (observed between 50 and 150 kHz). Both instabilities were measured with surface pressure sensors and were captured with high-speed schlieren. Linear stability analysis results agreed well with these measured instabilities in terms of both peak frequencies and amplification rates. Lower-frequency fluctuations were also noted in the schlieren data. Bicoherence analysis revealed nonlinear phase-locking between the shear-layer and second-mode instabilities. For the first time in axisymmetric, low-disturbance flow, naturally generated intermittent turbulent spots were observed in the reattached boundary layer. These spots appeared to evolve from shear-layer-instability wave packets convecting downstream. This work presents novel experimental evidence of the hypersonic shear-layer instability contributing directly to transition onset for an axisymmetric model.

