Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-29T07:33:30.804Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability wave–streak interactions in a high Mach number boundary layer at flight conditions

Published online by Cambridge University Press:  06 November 2018

Pedro Paredes Open the ORCID record for Pedro Paredes [Opens in a new window] ,
Meelan M. Choudhari  and
Fei Li
Pedro Paredes*
Affiliation:
Computational AeroSciences Branch, NASA Langley Research Center, Hampton, VA 23681, USA National Institute of Aerospace, 100 Exploration Way, Hampton, VA 23666, USA
Meelan M. Choudhari
Affiliation:
Computational AeroSciences Branch, NASA Langley Research Center, Hampton, VA 23681, USA
Fei Li
Affiliation:
Computational AeroSciences Branch, NASA Langley Research Center, Hampton, VA 23681, USA
*
†Email address for correspondence: pedro.paredes@nasa.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

The interaction of stationary streaks undergoing non-modal growth with modally unstable instability waves in a high Mach number boundary-layer flow is studied using numerical computations. The geometry and flow conditions are selected to match a relevant trajectory location from the ascent phase of the HIFiRE-1 flight experiment; namely, a $7^{\circ }$ half-angle, circular cone with 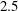$2.5$ mm nose radius, free-stream Mach number equal to 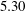$5.30$, unit Reynolds number equal to 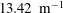$13.42~\text{m}^{-1}$ and wall-to-adiabatic temperature ratio of approximately 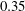$0.35$ over most of the vehicle. This paper investigates the nonlinear evolution of initially linear optimal disturbances that evolve into finite-amplitude streaks, followed by an analysis of the modal instability characteristics of the perturbed, streaky boundary-layer flow. The investigation is performed with a stationary, full Navier–Stokes equations solver and the plane-marching parabolized stability equations (PSE), in conjunction with partial-differential-equation-based planar eigenvalue analysis. The overall effect of streaks is to reduce the peak amplification factors of instability waves, indicating a possible downstream shift in the onset of laminar–turbulent transition. The present study confirms previous findings that the mean-flow distortion of the nonlinear streak perturbation reduces the amplification rates of the Mack-mode instability. More importantly, however, the present results demonstrate that the spanwise varying component of the streak can produce a larger effect on the Mack-mode amplification. The analysis of planar and oblique Mack-mode waves modulated by the presence of the streaks shows that the planar Mack mode still dominates the instability characteristics of the flow. The study with selected azimuthal wavenumbers for the stationary streaks reveals that a wavenumber of approximately 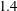$1.4$ times larger than the optimal wavenumber is more effective in stabilizing the planar Mack-mode instabilities. In the absence of unstable first-mode waves for the present cold-wall condition, transition onset is expected to be delayed until the peak streak amplitude increases to nearly 35 % of the free-stream velocity, when intrinsic instabilities of the boundary-layer streaks begin to dominate the transition process. For streak amplitudes below that limit a significant net stabilization is achieved, yielding a potential transition delay that can exceed 100 % of the length of the laminar region in the uncontrolled case.

JFM classification

Boundary Layers: Boundary layer stability Flow Control: Flow Control Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 858 , 10 January 2019 , pp. 474 - 499
Check for updates
Copyright
© Cambridge University Press 2018. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. S. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.Google Scholar
Bagheri, S. & Hanifi, A. 2007 The stabilizing effect of streaks on Tollmien–Schlichting and oblique waves: a parametric study. Phys. Fluids 19, 078103.Google Scholar
Boiko, A. V., Westin, K. J. A., Klingmann, B. G. B., Kozlov, V. V. & Alfredsson, P. H. 1994 Experiments in a boundary layer subjected to free stream turbulence. Part 2. The role of TS-waves in the transition process. J. Fluid Mech. 281, 219–245.Google Scholar
Choudhari, M., Li, F. & Edwards, J.2009 Stability analysis of roughness array wake in a high-speed boundary layer. AIAA Paper 2009-0170.Google Scholar
Choudhari, M., Li, F., Paredes, P. & Duan, L.2017 Computations of crossflow instability in hypersonic boundary layers. AIAA Paper 2017–4300.Google Scholar
Choudhari, M., Li, F., Paredes, P. & Duan, L.2018 Nonlinear evolution and breakdown of azimuthally compact crossflow vortex pattern over a yawed cone. AIAA Paper 2018-1823.Google Scholar
Chu, B.-T. 1956 On the energy transfer to small disturbances in fluid flow (Part I). Acta Mechanica 1 (3), 215–234.Google Scholar
Cossu, C. & Brandt, L. 2002 Stabilization of Tollmien–Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 14 (8), L57–L60.Google Scholar
De Tullio, N., Paredes, P., Sandham, N. D. & Theofilis, V. 2013 Roughness-induced instability and breakdown to turbulence in a supersonic boundary-layer. J. Fluid Mech. 735, 613–646.Google Scholar
Dennisen, N. & White, E.2011 Secondary instability of roughness wakes and optimal disturbances. AIAA Paper 2011-562.Google Scholar
Fong, K. D., Wang, X., Huang, Y., Zhong, X., McKiernan, G. R., Fisher, R. A. & Schneider, S. P. 2015 Second mode suppression in hypersonic boundary layer by roughness: design and experiments. AIAA J. 53 (10), 3138–3143.Google Scholar
Fong, K. D., Wang, X. & Zhong, X. 2014 Numerical simulation of roughness effect on the stability of a hypersonic boundary layer. Comput. Fluids 96, 350–367.Google Scholar
Fransson, J. H., Talamelli, A., Brandt, L. & Cossu, C. 2006 Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 96, 064501.Google Scholar
Fujii, K. 2006 Experiment of the two-dimensional roughness effect of hypersonic boundary-layer transition. J. Spacecr. Rockets 43 (4), 731–738.Google Scholar
Grossir, G., Musutti, D. & Chazot, O.2015 Flow characterization and boundary layer transition studies in VKI hypersonic facilities. AIAA Paper 2015-0578.Google Scholar
Hanifi, A., Schmid, P. J. & Henningson, D. S. 1996 Transient growth in compressible boundary layer flow. Phys. Fluids 8, 51–65.Google Scholar
Hermanns, M. & Hernández, J. A. 2008 Stable high-order finite-difference methods based on non-uniform grid point distributions. Intl J. Numer. Meth. Fluids 56, 233–255.Google Scholar
Holloway, P. F. & Sterrett, J. R.1964 Effect of controlled surface roughness on boundary-layer transition and heat transfer at Mach number of 4.8 and 6.0. NASA TR-D-2054.Google Scholar
James, C. S.1959 Boundary-layer transition on hollow cylinders in supersonic free flight as affected by Mach number and a screwthread type of surface roughness. NASA TR-Memo-1-20-59A.Google Scholar
Kimmel, R., Adamczak, D., Gaitonde, D., Rougeux, A. & Haynes, J. R.2007 HIFiRE-1 boundary layer transition experiment design. AIAA Paper 2007-0534.Google Scholar
Kimmel, R., Adamczak, D., Paull, A., Paull, R., Shannon, J., Pietsch, R., Frost, M. & Alesi, H. 2015 HIFiRE-1 ascent-phase boundary-layer transition. J. Spacecr. Rockets 52 (1), 217–230.Google Scholar
Klebanoff, P. S. 1971 Effect of free-stream turbulence on the laminar boundary layer. Bull. Am. Phys. Soc. 16, 1323.Google Scholar
Li, F., Choudhari, M., Chang, C. L., Kimmel, R., Adamczak, D. & Smith, M. 2015a Transition analysis for the ascent phase of HIFiRE-1 flight experiment. J. Spacecr. Rockets 52 (5), 1283–1293.Google Scholar
Li, F., Choudhari, M., Chang, C.-L., Greene, P. & Wu, M.2010 Development and breakdown of Gortler vortices in high speed boundary layers. AIAA Paper 2010-0705.Google Scholar
Li, F., Choudhari, M., Paredes, P. & Duan, L.2015b Secondary instability of stationary crossflow vortices in Mach 6 boundary layer over a circular cone. NASA TM-2015-218997.Google Scholar
Li, F., Choudhari, M., Paredes, P. & Duan, L. 2016 High-frequency instabilities of stationary crossflow vortices in a hypersonic boundary layer. Phys. Rev. Fluids 1, 053603.Google Scholar
Li, F. & Malik, M. R. 1996 On the nature of the PSE approximation. Theor. Comp. Fluid Dyn. 8, 253–273.Google Scholar
Li, F. & Malik, M. R. 1997 Spectral analysis of parabolized stability equations. Compt. Fluids 26 (3), 279–297.Google Scholar
Litton, D. K., Edwards, J. R. & White, J. A.2003 Algorithmic enhancements to the VULCAN Navier–Stokes solver. AIAA Paper 2003-3979.Google Scholar
Mack, L. M. 1984 Boundary layer linear stability theory. In AGARD–R–709 Special Course on Stability and Transition of Laminar Flow, pp. 3.1–3.81. North Atlantic Treaty Organization.Google Scholar
Mack, L. M.1969 Boundary layer stability theory. Tech. Rep. 900-277. Jet Propulsion Lab.Google Scholar
Malik, M. R., Li, F., Choudhari, M. M. & Chang, C.-L. 1999 Secondary instability of crossflow vortices and swept-wing boundary-layer transition. J. Fluid Mech. 399, 85–115.Google Scholar
Paredes, P.2014 Advances in global instability computations: from incompressible to hypersonic flow. PhD thesis, Universidad Politécnica de Madrid.Google Scholar
Paredes, P., Choudhari, M. M. & Li, F.2016a Nonlinear transient growth and boundary layer transition. AIAA Paper 2016-3956.Google Scholar
Paredes, P., Choudhari, M. & Li, F.2016b Transition delay in hypersonic boundary layers via optimal perturbations. NASA TM-2016-219210.Google Scholar
Paredes, P., Choudhari, M. M. & Li, F. 2016c Transition due to streamwise streaks in a supersonic flat plate boundary layer. Phys. Rev. Fluids 1, 083601.Google Scholar
Paredes, P., Choudhari, M. M. & Li, F. 2017a Instaiblity wave–streak interactions in a supersonic boundary layer. J. Fluid Mech. 831, 524–553.Google Scholar
Paredes, P., Choudhari, M. & Li, F.2017b Stabilization of hypersonic boundary layers by linear and nonlinear optimal perturbations. AIAA Paper 2017-3634.Google Scholar
Paredes, P., Choudhari, M. & Li, F.2017c Transient growth and streak instabilities on a hypersonic blunt body. AIAA Paper 2017-0066.Google Scholar
Paredes, P., Choudhari, M. M., Li, F. & Chang, C.-L. 2016d Optimal growth in hypersonic boundary layers. AIAA J. 54 (10), 3050–3061.Google Scholar
Paredes, P., De Tullio, N., Sandham, N. D. & Theofilis, V. 2015a Instability study of the wake behind a discrete roughness element in a hypersonic boundary layer. In Instability and Control of Massively Separated Flows (ed. Theofilis, Vassilis & Soria, Julio), pp. 91–96. Springer International Publishing.Google Scholar
Paredes, P., Hanifi, A., Theofilis, V. & Henningson, D. 2015b The nonlinear PSE-3D concept for transition prediction in flows with a single slowly-varying spatial direction. Procedia IUTAM 14C, 35–44.Google Scholar
Paredes, P., Hermanns, M., Le Clainche, S. & Theofilis, V. 2013 Order 104 speedup in global linear instability analysis using matrix formation. Comput. Meth. Appl. Mech. Engng 253, 287–304.Google Scholar
Pralits, J. O., Airiau, C., Hanifi, A. & Henningson, D. S. 2000 Sensitivity analysis using adjoint parabolized stability equations for compressible flows. Flow Turbul. Combust. 65, 183–210.Google Scholar
Ren, J., Fu, S. & Hanifi, A. 2016 Stabilization of the hypersonic boundary layer by finite-amplitude streaks. Phys. Fluids 28, 024110.Google Scholar
Rumsey, C. L., Biedron, R. T. & Thomas, J. L.1997 CFL3D: Its history and some recent applications. NASA TM-112861.Google Scholar
Schlichting, H. 1979 Boundary Layer Theory. McGraw-Hill.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Shahinfar, S., Sattarzadeh, S. S., Fransson, J. H. & Talamelli, A. 2012 Revival of classical vortex generators now for transition delay. Phys. Rev. Lett. 109, 074501.Google Scholar
Tumin, A. & Reshotko, E. 2003 Optimal disturbances in compressible boundary layers. AIAA J. 41, 2357–2363.Google Scholar
Vermeersch, O. & Arnal, D. 2010 Klebanoff-mode modeling and bypass-transition prediction. AIAA J. 48 (11), 2491–2500.Google Scholar
Zuccher, S., Tumin, A. & Reshotko, E. 2006 Parabolic approach to optimal perturbations in compressible boundary layers. J. Fluid Mech. 556, 189–216.Google Scholar