Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-14T07:10:46.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral properties of turbulent-kinetic-energy production and dissipation in turbulent wall-bounded flows

Published online by Cambridge University Press:  10 September 2018

Tie Wei Open the ORCID record for Tie Wei [Opens in a new window]
Tie Wei*
Affiliation:
Department of Mechanical Engineering, New Mexico Institute of Mining and Technology, Socorro, NM 87801, USA
*
†Email address for correspondence: tie.wei@nmt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Turbulent-kinetic-energy (TKE) production 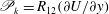$\mathscr{P}_{k}=R_{12}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)$ and TKE dissipation 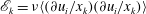$\mathscr{E}_{k}=\unicode[STIX]{x1D708}\langle (\unicode[STIX]{x2202}u_{i}/x_{k})(\unicode[STIX]{x2202}u_{i}/x_{k})\rangle$ are important quantities in the understanding and modelling of turbulent wall-bounded flows. Here 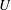$U$ is the mean velocity in the streamwise direction, 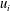$u_{i}$ or 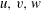$u,v,w$ are the velocity fluctuation in the streamwise $x$- direction, wall-normal 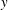$y$- direction, and spanwise $z$-direction, respectively; $\unicode[STIX]{x1D708}$ is the kinematic viscosity; 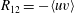$R_{12}=-\langle uv\rangle$ is the kinematic Reynolds shear stress. Angle brackets denote Reynolds averaging. This paper investigates the integral properties of TKE production and dissipation in turbulent wall-bounded flows, including turbulent channel flows, turbulent pipe flows and zero-pressure-gradient turbulent boundary layer flows (ZPG TBL). The main findings of this work are as follows. (i) The global integral of TKE production is predicted by the RD identity derived by Renard & Deck (J. Fluid Mech., vol. 790, 2016, pp. 339–367) as 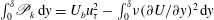$\int _{0}^{\unicode[STIX]{x1D6FF}}\mathscr{P}_{k}\,\text{d}y=U_{b}u_{\unicode[STIX]{x1D70F}}^{2}-\int _{0}^{\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D708}(\unicode[STIX]{x2202}U/\unicode[STIX]{x2202}y)^{2}\,\text{d}y$ for channel flows, where 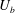$U_{b}$ is the bulk mean velocity, 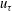$u_{\unicode[STIX]{x1D70F}}$ is the friction velocity and 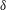$\unicode[STIX]{x1D6FF}$ is the channel half-height. Using inner scaling, the identity for the global integral of the TKE production in channel flows is 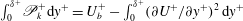$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\text{d}y^{+}=U_{b}^{+}-\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}(\unicode[STIX]{x2202}U^{+}/\unicode[STIX]{x2202}y^{+})^{2}\,\text{d}y^{+}$. In the present work, superscript 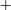$+$ denotes inner scaling. At sufficiently high Reynolds number, the global integral of the TKE production in turbulent channel flows can be approximated as 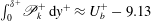$\int _{0}^{\unicode[STIX]{x1D6FF}^{+}}\mathscr{P}_{k}^{+}\,\text{d}y^{+}\approx U_{b}^{+}-9.13$. (ii) At sufficiently high Reynolds number, the integrals of TKE production and dissipation are equally partitioned around the peak Reynolds shear stress location 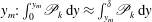$y_{m}:\,\int _{0}^{y_{m}}\mathscr{P}_{k}\,\text{d}y\approx \int _{y_{m}}^{\unicode[STIX]{x1D6FF}}\mathscr{P}_{k}\,\text{d}y$ and 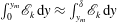$\int _{0}^{y_{m}}\mathscr{E}_{k}\,\text{d}y\approx \int _{y_{m}}^{\unicode[STIX]{x1D6FF}}\mathscr{E}_{k}\,\text{d}y$. (iii) The integral of the TKE production 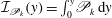${\mathcal{I}}_{\mathscr{P}_{k}}(y)=\int _{0}^{y}\mathscr{P}_{k}\,\text{d}y$ and the integral of the TKE dissipation 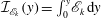${\mathcal{I}}_{\mathscr{E}_{k}}(y)=\int _{0}^{y}\mathscr{E}_{k}\,\text{d}y$ exhibit a logarithmic-like layer similar to that of the mean streamwise velocity as, for example, 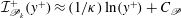${\mathcal{I}}_{\mathscr{P}_{k}}^{+}(y^{+})\approx (1/\unicode[STIX]{x1D705})\ln (y^{+})+C_{\mathscr{P}}$ and 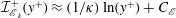${\mathcal{I}}_{\mathscr{E}_{k}}^{+}(y^{+})\approx (1/\unicode[STIX]{x1D705})\ln (y^{+})+C_{\mathscr{E}}$, where $\unicode[STIX]{x1D705}$ is the von Kármán constant, 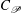$C_{\mathscr{P}}$ and 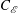$C_{\mathscr{E}}$ are addititve constants. The logarithmic-like scaling of the global integral of TKE production and dissipation, the equal partition of the integrals of TKE production and dissipation around the peak Reynolds shear stress location 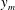$y_{m}$ and the logarithmic-like layer in the integral of TKE production and dissipation are intimately related. It is known that the peak Reynolds shear stress location 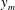$y_{m}$ scales with a meso-length scale 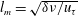$l_{m}=\sqrt{\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}}}$. The equal partition of the integral of the TKE production and dissipation around 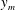$y_{m}$ underlines the important role of the meso-length scale 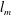$l_{m}$ in the dynamics of turbulent wall-bounded flows.

JFM classification

Boundary Layers: Boundary layer structure Boundary Layers: Boundary Layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , pp. 449 - 473
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H. & Antonia, R. A. 2009 Near-wall similarity between velocity and scalar fluctuations in a turbulent channel flow. Phys. Fluids 21 (2), 025109.Google Scholar
Abe, H. & Antonia, R. A. 2016 Relationship between the energy dissipation function and the skin friction law in a turbulent channel flow. J. Fluid Mech. 798, 140–164.Google Scholar
Abe, H. & Antonia, R. A. 2017 Relationship between the heat transfer law and the scalar dissipation function in a turbulent channel flow. J. Fluid Mech. 830, 300–325.Google Scholar
Abe, H., Kawamura, H. & Matsuo, Y. 2001 Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. Trans. ASME J. Fluids Engng 123 (2), 382–393.Google Scholar
Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Arch. Appl. Mech. 52 (6), 355–377.Google Scholar
Afzal, N. 1984 Mesolayer theory for turbulent flows. AIAA J. 22 (3), 437–439.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.Google Scholar
Cantwell, B. J. 1981 Organized motion in turbulent flow. Annu. Rev. Fluid Mech. 13 (1), 457–515.Google Scholar
De Graaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Eggels, J. G. M., Unger, F., Weiss, M. H., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–210.Google Scholar
El Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91 (3), 475–495.Google Scholar
Fernholz, H. H. & Finley, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32 (4), 245–311.Google Scholar
Fife, P., Klewicki, J., McMurtry, P. & Wei, T. 2005a Multiscaling in the presence of indeterminacy: wall-induced turbulence. Multiscale Model. Simul. 4 (3), 936–959.Google Scholar
Fife, P., Wei, T., Klewicki, J. & McMurtry, P. 2005b Stress gradient balance layers and scale hierarchies in wall-bounded turbulent flows. J. Fluid Mech. 532, 165–189.Google Scholar
Fukagata, K., Iwamoto, K. & Kasagi, N. 2002 Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 14 (11), L73–L76.Google Scholar
Gad-el Hak, M. & Bandyopadhyay, P. R. 1994 Reynolds number effects in wall-bounded turbulent flows. Appl. Mech. Rev. 47 (8), 307–365.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20 (10), 101511.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. & Smits, A. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108 (9), 094501.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. & Smits, A. 2013 Logarithmic scaling of turbulence in smooth-and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.Google Scholar
Iwamoto, K., Suzuki, Y. & Kasagi, N. 2002 Reynolds number effect on wall turbulence: toward effective feedback control. Intl J. Heat Fluid Flow 23 (5), 678–689.Google Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2009 Comparison of turbulent boundary layers and channels from direct numerical simulation. In TSFP Digital Library Online. Begel House Inc.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. Trans. ASME J. Fluids Engng 132 (9), 094001.Google Scholar
Laadhari, F. 2007 Reynolds number effect on the dissipation function in wall-bounded flows. Phys. Fluids 19 (3), 038101.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re = 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Long, R. R. & Chen, T.-C. 1981 Experimental evidence for the existence of the mesolayer in turbulent systems. J. Fluid Mech. 105, 19–59.Google Scholar
Marusic, I., Baars, W. J. & Hutchins, N. 2017 Scaling of the streamwise turbulence intensity in the context of inner-outer interactions in wall turbulence. Phys. Rev. Fluids 2 (10), 100502.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010b Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21 (11), 111703.Google Scholar
Monty, J. P., Hutchins, N., Ng, H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20 (10), 101518.Google Scholar
Ng, H., Monty, J., Hutchins, N., Chong, M. S. & Marusic, I. 2011 Comparison of turbulent channel and pipe flows with varying Reynolds number. Exp. Fluids 51 (5), 1261–1281.Google Scholar
Orlandi, P. 1997 Helicity fluctuations and turbulent energy production in rotating and non-rotating pipes. Phys. Fluids 9 (7), 2045–2056.Google Scholar
Panton, R. L. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37 (4), 341–383.Google Scholar
Perry, A. E., Marusic, I. & Jones, M. B. 2002 On the streamwise evolution of turbulent boundary layers in arbitrary pressure gradients. J. Fluid Mech. 461, 61–91.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2016 Passive scalars in turbulent channel flow at high Reynolds number. J. Fluid Mech. 788, 614–639.Google Scholar
Pope, S. B. 2001 Turbulent Flows. Cambridge University Press.Google Scholar
Renard, N. & Deck, S. 2016 A theoretical decomposition of mean skin friction generation into physical phenomena across the boundary layer. J. Fluid Mech. 790, 339–367.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.Google Scholar
Simens, M. P., Jiménez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228 (11), 4218–4231.Google Scholar
Smits, A. J. & Marusic, I. 2013 Wall-bounded turbulence. Phys. Today 66 (9), 25–30.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Sreenivasan, K. R. 1989 The turbulent boundary layer. In Frontiers in Experimental Fluid Mechanics, pp. 159–209. Springer.Google Scholar
Sreenivasan, K. R. & Sahay, A. 1997 The persistence of viscous effects in the overlap region, and the mean velocity in turbulent pipe and channel flows. In Self-Sustaining Mechanisms of Wall Turbulence (ed. Panton, R.), Advances in Fluid Mechanics, vol. 15, pp. 253–272. Computational Mechanics Publications, Southampton, UK.Google Scholar
Tsuji, Y. 1999 Peak position of dissipation spectrum in turbulent boundary layers. Phys. Rev. E 59 (6), 7235.Google Scholar
Vallikivi, M., Hultmark, M. & Smits, A. J. 2015 Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.Google Scholar
Vincenti, P., Klewicki, J., Morrill-Winter, C., White, C. M. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp. Fluids 54 (12), 1629.Google Scholar
Wei, T., Fife, P., Klewicki, J. & McMurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Wei, T. & Willmarth, W. W. 1989 Reynolds-number effects on the structure of a turbulent channel flow. J. Fluid Mech. 204, 57–95.Google Scholar
Wosnik, M., Castillo, L. & George, W. K. 2000 A theory for turbulent pipe and channel flows. J. Fluid Mech. 421, 115–145.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.Google Scholar
Zanoun, E.-S., Nagib, H. & Durst, F. 2009 Refined cf relation for turbulent channels and consequences for high-Re experiments. Fluid Dyn. Res. 41 (2), 021405.Google Scholar