Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T07:19:57.012Z Has data issue: false hasContentIssue false
  • English
  • Français

The intense vorticity structures near the turbulent/non-turbulent interface in a jet

Published online by Cambridge University Press:  05 September 2011

Carlos B. da Silva ,
Ricardo J. N. dos Reis  and
José C. F. Pereira
Carlos B. da Silva*
Affiliation:
IDMEC/IST, Technical University of Lisbon, Pav. Mecânica I, 1° andar/esq./LASEF, Av. Rovisco Pais, 1049-001 Lisboa, Portugal
Ricardo J. N. dos Reis
Affiliation:
IDMEC/IST, Technical University of Lisbon, Pav. Mecânica I, 1° andar/esq./LASEF, Av. Rovisco Pais, 1049-001 Lisboa, Portugal
José C. F. Pereira
Affiliation:
IDMEC/IST, Technical University of Lisbon, Pav. Mecânica I, 1° andar/esq./LASEF, Av. Rovisco Pais, 1049-001 Lisboa, Portugal
*
†Email address for correspondence: Carlos.Silva@ist.utl.pt
Get access Rights & Permissions [Opens in a new window]

Abstract

The characteristics of the intense vorticity structures (IVSs) near the turbulent/non-turbulent (T/NT) interface separating the turbulent and the irrotational flow regions are analysed using a direct numerical simulation (DNS) of a turbulent plane jet. The T/NT interface is defined by the radius of the large vorticity structures (LVSs) bordering the jet edge, while the IVSs arise only at a depth of about 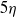from the T/NT interface, where 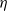is the Kolmogorov micro-scale. Deep inside the jet shear layer the characteristics of the IVSs are similar to the IVSs found in many other flows: the mean radius, tangential velocity and circulation Reynolds number are 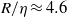, , 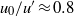and 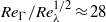, where 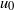, and 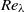are the root mean square of the velocity fluctuations and the Reynolds number based on the Taylor micro-scale, respectively. Moreover, as in forced isotropic turbulence the IVSs inside the jet are well described by the Burgers vortex model, where the vortex core radius is stable due to a balance between the competing effects of axial vorticity production and viscous diffusion. Statistics conditioned on the distance from the T/NT interface are used to analyse the effect of the T/NT interface on the geometry and dynamics of the IVSs and show that the mean radius 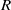, tangential velocity 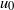and circulation 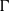of the IVSs increase as the T/NT interface is approached, while the vorticity norm 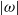stays approximately constant. Specifically , and 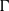exhibit maxima at a distance of roughly one Taylor micro-scale from the T/NT interface, before decreasing as the T/NT is approached. Analysis of the dynamics of the IVS shows that this is caused by a sharp decrease in the axial stretching rate acting on the axis of the IVSs near the jet edge. Unlike the IVSs deep inside the shear layer, there is a small predominance of vortex diffusion over stretching for the IVSs near the T/NT interface implying that the core of these structures is not stable i.e. it will tend to grow in time. Nevertheless the Burgers vortex model can still be considered to be a good representation for the IVSs near the jet edge, although it is not as accurate as for the IVSs deep inside the jet shear layer, since the observed magnitude of this imbalance is relatively small.

JFM classification

Boundary Layers: Free shear layers Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 685 , 25 October 2011 , pp. 165 - 190
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Anand, R. K., Boersma, B. J. & Agrawal, A. 2009 Detection of turbulent/non-turbulent interface for an axisymmetric turbulent jet: evaluation of known criteria and proposal of a new criterion. Exp. Fluids 47 (6), 995–1007.CrossRefGoogle Scholar
2. Antonia, R. A., Satyaprakash, B. R. & Hussain, A. K. M. F. 1980 Measurements of dissipation rate and some other characteristics of turbulent plane and circular jets. Phys. Fluids 23 (4), 695–700.CrossRefGoogle Scholar
3. Ashust, W., Kerstein, A., Kerr, R. & Gibson, C. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30, 2343.CrossRefGoogle Scholar
4. Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
5. Corrsin, S. & Kistler, A. L. 1955 Free-stream boundaries of turbulent flows. NACA Tech Rep. TN-1244.Google Scholar
6. Davidson, P. A. 2004 Turbulence, an Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
7. Deo, R. C., Mi, J. & Nathan, G. J. 2008 The influence of Reynolds number on a plane jet. Phys. Fluids 20, 075108.CrossRefGoogle Scholar
8. Dubief, I. & Delcayre, F. 2000 On coherent-vortex identification in turbulence. J. Turbul. 1 (011).CrossRefGoogle Scholar
9. Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.CrossRefGoogle Scholar
10. Holzner, M., Liberzon, A., Nikitin, N., Kinzelbach, W. & Tsinober, A. 2007 Small-scale aspects of flows in proximity of the turbulent/non-turbulent interface. Phys. Fluids 19, 071702.CrossRefGoogle Scholar
11. Hunt, J. C. R., Eames, I. & Westerweel, J. 2008 Vortical interactions with interfacial shear layers. In Proceedings of IUTAM Conference on Computational Physics and New Perspectives in Turbulence, Nagoya, September 2006 (ed. Kaneda, Y. ). Springer Science.Google Scholar
12. Hunt, J. C. R., Eames, I., Westerweel, J., Davidson, P. A., Voropayev, S., Fernando, J. & Braza, M. 2010 Thin shear layers – the key to turbulence structure. J. Hydro-Environment Research 4, 75–82.CrossRefGoogle Scholar
13. Jiménez, J. & Wray, A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.CrossRefGoogle Scholar
14. Jiménez, J., Wray, A., Saffman, P. & Rogallo, R. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
15. Kang, S.-J., Tanahashi, M. & Miyauchi, T. 2008 Dynamics of fine scale eddy clusters in turbulent channel flows. J. Turbul. 8 (52), 1–19.Google Scholar
16. Kida, S. & Miura, H. 1998 Identification and analysis of vortical structures. Eur. J. Mech. (B/Fluids) 17 (4), 471–489.CrossRefGoogle Scholar
17. Lesieur, M. 1997 Turbulence in Fluids, 3rd edn. Kluwer.CrossRefGoogle Scholar
18. Mathew, J. & Basu, A. 2002 Some characteristics of entrainment at a cylindrical turbulent boundary. Phys. Fluids 14 (7), 2065–2072.CrossRefGoogle Scholar
19. Mouri, H., Houri, A. & Kawashima, Y. 2007 Laboratory experiments for intense vortical structures in turbulence velocity fields. Phys. Fluids 19, 055101.CrossRefGoogle Scholar
20. Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
21. Siggia, E. D. 1981 Numerical study of small-scale intermittency in three-dimensional turbulence. J. Fluid Mech. 107, 375–406.CrossRefGoogle Scholar
22. da Silva, C. B. 2009 The behavior of subgrid-scale models near the turbulent/nonturbulent interface in jets. Phys. Fluids 21, 081702.CrossRefGoogle Scholar
23. da Silva, C. B. & Pereira, J. C. F. 2007a Analysis of the gradient-diffusion hypothesis in large-eddy simulations based on transport equations. Phys. Fluids 19, 035106.CrossRefGoogle Scholar
24. da Silva, C. B. & Pereira, J. C. F. 2007 b Enstrophy, strain and scalar gradient dynamics across the turbulent–nonturbulent interface in jets. In Advances in Turbulence XI – 11th Euromech ETC, Porto.CrossRefGoogle Scholar
25. da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20, 055101.CrossRefGoogle Scholar
26. da Silva, C. B. & Pereira, J. C. F. 2009 Erratum: ‘invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets’ [Phys. Fluids 20, 055101 (2008)]. Phys. Fluids 21, 019902.CrossRefGoogle Scholar
27. da Silva, C. B. & dos Reis, R. N. 2011 The role of coherent vortices near the turbulent/nonturbulent interface in a planar jet. Phil. Trans. R. Soc. A 369, 738–753.CrossRefGoogle Scholar
28. da Silva, C. B. & Taveira, R. R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22, 121702.CrossRefGoogle Scholar
29. Stanley, S., Sarkar, S. & Mellado, J. P. 2002 A study of the flowfield evolution and mixing in a planar turbulent jet using direct numerical simulation. J. Fluid Mech. 450, 377–407.CrossRefGoogle Scholar
30. Tanahashi, M., Iwase, S. & Miyauchi, T. 2001 Appearance and alignment with strain rate of coherent fine scale eddies in turbulent mixing layer. J. Turbul. 2 (6), 1–17.CrossRefGoogle Scholar
31. Townsend, A. A. 1966 The mechanism of entrainment in free turbulent flows. J. Fluid Mech. 26, 689–715.CrossRefGoogle Scholar
32. Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
33. Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.CrossRefGoogle Scholar
34. Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent-nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.CrossRefGoogle ScholarPubMed
35. Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.CrossRefGoogle Scholar