Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T05:12:15.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction between mountain waves and shear flow in an inertial layer

Published online by Cambridge University Press:  06 March 2017

Jin-Han Xie Open the ORCID record for Jin-Han Xie [Opens in a new window]  and
Jacques Vanneste
Jin-Han Xie*
Affiliation:
Department of Physics, University of California, Berkeley, CA 94720, USA
Jacques Vanneste
Affiliation:
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, Edinburgh EH9 3FD, UK
*
†Email address for correspondence: j.h.xie@berkeley.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Mountain-generated inertia–gravity waves (IGWs) affect the dynamics of both the atmosphere and the ocean through the mean force they exert as they interact with the flow. A key to this interaction is the presence of critical-level singularities or, when planetary rotation is taken into account, inertial-level singularities, where the Doppler-shifted wave frequency matches the local Coriolis frequency. We examine the role of the latter singularities by studying the steady wavepacket generated by a multiscale mountain in a rotating linear shear flow at low Rossby number. Using a combination of Wentzel–Kramers–Brillouin (WKB) and saddle-point approximations, we provide an explicit description of the form of the wavepacket, of the mean forcing it induces and of the mean-flow response. We identify two distinguished regimes of wave propagation: Regime I applies far enough from a dominant inertial level for the standard ray-tracing approximation to be valid; Regime II applies to a thin region where the wavepacket structure is controlled by the inertial-level singularities. The wave–mean-flow interaction is governed by the change in Eliassen–Palm (or pseudomomentum) flux. This change is localised in a thin inertial layer where the wavepacket takes a limiting form of that found in Regime II. We solve a quasi-geostrophic potential-vorticity equation forced by the divergence of the Eliassen–Palm flux to compute the wave-induced mean flow. Our results, obtained in an inviscid limit, show that the wavepacket reaches a large-but-finite distance downstream of the mountain (specifically, a distance of order 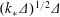$(k_{\ast }\unicode[STIX]{x1D6E5})^{1/2}\unicode[STIX]{x1D6E5}$, where 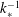$k_{\ast }^{-1}$ and 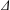$\unicode[STIX]{x1D6E5}$ measure the wave and envelope scales of the mountain) and extends horizontally over a similar scale.

JFM classification

Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Topographic effects Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , pp. 352 - 380
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexander, M. J., Geller, M., McLandress, C., Polavarapu, S., Preusse, P., Sassi, F., Sato, K., Eckermann, S., Ern, M., Hertzog, A. et al. 2010 Recent developments in gravity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models. Q. J. R. Meteorol. Soc. 136 (650), 1103–1124.CrossRefGoogle Scholar
Andrews, D. G. & McIntyre, M. E. 1976 Planetary waves in horizontal and vertical shear: the generalized Eliassen–Palm relation and the mean zonal acceleration. J. Atmos. Sci. 33, 2031–2048.2.0.CO;2>CrossRefGoogle Scholar
Andrews, D. G. & McIntyre, M. E. 1978 Generalized Eliassen–Palm and Charney–Drazin theorems for waves on axisymmetric mean flows in compressible atmospheres. J. Atmos. Sci. 35, 175–185.Google Scholar
Bender, C. M. & Orszag, S. A. 1999 Advanced Mathematical Methods for Scientists and Engineers: Asymptotic Methods and Perturbation Theory. Springer.Google Scholar
Booker, J. R. & Bretherton, F. P. 1967 The critical layer for internal gravity waves in a shear flow. J. Fluid Mech. 27, 513–539.Google Scholar
Boyd, J. P. 1976 The noninteraction of waves with the zonally averaged flow on a spherical earth and the interrelationships on eddy fluxes of energy, heat and momentum. J. Atmos. Sci. 33, 2285–2291.2.0.CO;2>CrossRefGoogle Scholar
Bretherton, F. 1969a On the mean motion induced by internal gravity waves. J. Fluid Mech. 36, 758–803.Google Scholar
Bretherton, F. P. 1966 The propagation of groups of internal gravity waves in a shear flow. Q. J. R. Meteorol. Soc. 92, 466–480.CrossRefGoogle Scholar
Bretherton, F. P. 1969b Momentum transport by gravity waves. Q. J. R. Meteorol. Soc. 95, 213–243.Google Scholar
Charney, J. G. & Drazin, P. G. 1961 Propagation of planetary-scale disturbances from the lower into the upper atmosphere. J. Geophys. Res. 66, 83–109.CrossRefGoogle Scholar
Edmon, H. J. Jr, Hoskins, B. J. & McIntyre, M. E. 1980 Eliassen–Palm cross sections for the troposphere. J. Atmos. Sci. 37, 2600–2616.Google Scholar
Eliassen, A. & Palm, E. 1961 On the transfer of energy in stationary mountain waves. Geophys. Publ. 22, 1–23.Google Scholar
Fritts, D. C. & Alexander, M. J. 2003 Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 41, 1003.CrossRefGoogle Scholar
Hasha, A., Bühler, O. & Scinocca, J. 2008 Gravity wave refraction by three-dimensionally varying winds and the global transport of angular momentum. J. Atmos. Sci. 65, 2892–2906.Google Scholar
Jones, W. L. 1967 Propagation of internal gravity waves in fluids with shear flow and rotation. J. Fluid Mech. 30, 439–448.Google Scholar
Lott, F., Millet, C. & Vanneste, J. 2015 Inertia-gravity waves in inertially stable and unstable shear flows. J. Fluid Mech. 775, 223–240.Google Scholar
Lott, F., Plougonven, R. & Vanneste, J. 2010 Gravity waves generated by sheared potential vorticity anomalies. J. Atmos. Sci. 67, 157–170.Google Scholar
Lott, F., Plougonven, R. & Vanneste, J. 2012 Gravity waves generated by sheared three-dimensional potential vorticity anomalies. J. Atmos. Sci. 69, 2134–2151.CrossRefGoogle Scholar
Martin, A. & Lott, F. 2007 Synoptic responses to mountain gravity waves encountering directional critical levels. J. Atmos. Sci. 64, 828–848.Google Scholar
Nikurashin, M. & Ferrari, R. 2011 Global energy conversion rate from geostrophic flows into internal lee waves in the deep ocean. Geophys. Res. Lett. 38, L08610.CrossRefGoogle Scholar
Nikurashin, M. & Ferrari, R. 2013 Overturning circulation driven by breaking internal waves in the deep ocean. Geophys. Res. Lett. 41, 3133–3137.Google Scholar
Plougonven, R. & Vanneste, J. 2010 Quasi-geostrophic dynamics of a finite-thickness tropopause. J. Atmos. Sci. 67, 3149–3163.Google Scholar
Scott, R. B., Goff, J. A., Garabato, A. C. N. & Nurser, A. J. G. 2011 Global rate and spectral characteristics of internal gravity wave generation by geostrophic flow over topography. J. Geophys. Res. 116, C09029.Google Scholar
Shutts, G. 1995 Gravity-wave drag parametrization over complex terrain: the effect of critical-level absorption in directional wind-shear. Q. J. R. Meteorol. Soc. 121, 1005–1021.Google Scholar
Shutts, G. 2001 A linear model of back-sheared flow over an isolated hill in the presence of rotation. J. Atmos. Sci. 58, 3293–3311.Google Scholar
Shutts, G. 2003 Inertia gravity wave and neutral Eady wave trains forced by directionally sheared flow over isolated hills. J. Atmos. Sci. 60, 593–606.Google Scholar
Yamanaka, M. D. & Tanaka, H. 1984 Propagation and breakdown of internal inertio-gravity waves near critical levels in the middle atmosphere. J. Met. Soc. Japan 62, 1–16.Google Scholar