Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T06:45:19.284Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction of a laminar vortex ring with a thin permeable screen

Published online by Cambridge University Press:  13 July 2012

Christian Naaktgeboren ,
Paul S. Krueger  and
José L. Lage
Christian Naaktgeboren
Affiliation:
Hydraulic Engineering, CFD, Andritz Hydro Ltd, Pointe-Claire, Québec, H9R 1B9, Canada
Paul S. Krueger*
Affiliation:
Department of Mechanical Engineering, Southern Methodist University, Dallas, TX 75275, USA
José L. Lage
Affiliation:
Department of Mechanical Engineering, Southern Methodist University, Dallas, TX 75275, USA
*
†Email address for correspondence: pkrueger@engr.smu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The canonical case of a vortex ring interacting with a solid surface orthogonal to its symmetry axis exhibits a variety of intricate behaviours, including stretching of the primary vortex ring and generation of secondary vorticity, which illustrate key features of vortex interactions with boundaries. Replacing the solid boundary with a permeable screen allows for new behaviour by relaxing the no-through-flow condition, and can provide a useful analogue for the interaction of large-scale vortices with permeable structures or closely spaced obstructions. The present investigation considers the interaction of experimentally generated vortex rings with a thin permeable screen. The vortex rings were generated using a piston-in-cylinder mechanism using piston stroke-to-diameter ratios (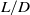) of 1.0 and 3.0 (nominal) with jet Reynolds numbers (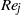) of 3000 and 6000 (nominal). Planar laser-induced fluorescence and digital particle image velocimetry (DPIV) were used to study the interaction with wire-mesh screens having surface open-area ratios (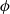) in the range 0.44–0.79. Solid surfaces (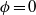) and free vortex rings (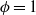) were also included as special cases. Measurement of the vortex trajectories showed expansion of the vortex ring diameter as it approached the boundary and generation of secondary vorticity similar to the case of a solid boundary, but the primary vortex diameter then began to contract towards the symmetry axis as the flow permeated the screen and reorganized into a transmitted vortex downstream. The trajectories were highly dependent on 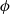, with little change in the incident ring trajectory for 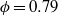. Measurement of the hydrodynamic impulse and kinetic energy using DPIV showed that the change between the average upstream and downstream values of these quantities also depended primarily on , with a slight decrease in the relative change as and/or 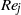were increased. The kinetic energy dissipation (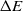) was much more sensitive to 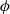, with a strongly nonlinear dependence, while the decrease in impulse (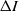) was nearly linear in 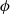. A simple model is proposed to relate and 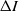in terms of bulk flow parameters. The model incorporates the decrease in flow velocity during the interaction due to the drag force exerted by the screen on the flow.

JFM classification

Low-Reynolds-number flows: Porous media Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 707 , 25 September 2012 , pp. 260 - 286
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adhikari, D. & Lim, T. T. 2009 The impact of a vortex ring on a porous screen. Fluid Dyn. Res. 41, 051404.Google Scholar
2. Boldes, U. & Ferreri, J. C. 1973 Behavior of vortex rings in the vicinity of a wall. Phys. Fluids 16, 2005–2006.CrossRefGoogle Scholar
3. Cerra, A. W. & Smith, C. R. 1983 Experimental observations of vortex ring interaction with the fluid adjacent to a surface. Tech. Rep. FM-4. Lehigh University, Bethlehem, PA.Google Scholar
4. Doligalski, T. L., Smith, C. R. & Walker, J. D. A. 1994 Vortex interactions with walls. Annu. Rev. Fluid Mech. 26, 573–616.CrossRefGoogle Scholar
5. Dyson, F. W. 1893 The potential of an anchor ring. Phil. Trans. R. Soc. Lond. A 184, 43–95.Google Scholar
6. Helmholtz, H. 1867 On integrals of the hydrodynamical equations, which express vortex-motion. Phil. Mag. 33, 485–512.Google Scholar
7. Hrynuk, J. T., Van Luipen, J. & Bohl, D. 2012 Flow visualization of a vortex ring interaction with porous surfaces. Phys. Fluids 24, 037103.CrossRefGoogle Scholar
8. Krueger, P. S. 2006 Measurement of propulsive power and evaluation of propulsive performance from the wake of a self-propelled vehicle. Bioinspir. Biomim. 1, S49–S56.CrossRefGoogle ScholarPubMed
9. Krueger, P. S. & Gharib, M. 2003 The significance of vortex ring formation to the impulse and thrust of a starting jet. Phys. Fluids 15, 1271–1281.CrossRefGoogle Scholar
10. Lim, T. T. & Nickels, T. B. 1995 Vortex rings. In Fluid Vortices (ed. Green, S. I. ), pp. 95–153. Kluwer.Google Scholar
11. Magarvey, R. H. & MacLatchy, C. S. 1963 The disintegration of vortex rings. Can. J. Phys. 42, 684–689.CrossRefGoogle Scholar
12. Maxworthy, T. 1972 The structure and stability of vortex rings. J. Fluid Mech. 51, 15–32.Google Scholar
13. Naaktgeboren, C. 2007 Interaction of pressure and momentum driven flows with thin porous media: experiments and modelling. PhD thesis, Southern Methodist University, Dallas, TX.Google Scholar
14. Naaktgeboren, C., Krueger, P. S. & Lage, J. L. 2006 Experimental investigation of vortex ring interaction with a permeable flat surface. In Proceedings of the 3rd International Conference on Applications of Porous Media (ed. A. Mojtabi & A. Mohamad), ICAPM, Paper No. 00015 (8 pp.).Google Scholar
15. Naaktgeboren, C., Krueger, P. S. & Lage, J. L. 2012 Inlet and outlet pressure-drop effects on the determination of permeabiliity and form coefficient of a porous medium. Trans. ASME I: J. Fluids Engng 134, paper no. 051209.Google Scholar
16. Naaktgeboren, C., Olcay, A. B., Krueger, P. S. & Lage, J. L. 2005 Vortex ring interaction with a permeable flat surface. Bull. Am. Phys. Soc. 50, 165.Google Scholar
17. Olcay, A. B. & Krueger, P. S. 2008 Measurement of ambient fluid entrainment during laminar vortex ring formation. Exp. Fluids 44, 235–247.Google Scholar
18. Orlandi, P. & Verzicco, R. 1993 Vortex rings impinging on walls: axisymmetric and three-dimensional simulations. J. Fluid Mech. 256, 615–646.Google Scholar
19. Oshima, Y. & Asaka, S. 1977 Interaction of multi-vortex rings. J. Phys. Soc. Japan 42, 1391–1395.Google Scholar
20. Saffman, P. G. 1992 Vortex Dynamics. Cambridge University Press.Google Scholar
21. Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24, 235–279.Google Scholar
22. Staymates, M. & Settles, G. 2005 Vortex ring impingement and particle suspension. Bull. Am. Phys. Soc. 50, 165–166.Google Scholar
23. Verzicco, R. & Orlandi, P. 1996 Wall/vortex-ring interactions. Appl. Mech. Rev. 49, 447–461.CrossRefGoogle Scholar
24. Walker, D. A. 1987 A fluorescence technique for measurement of concentration in mixing fluids. J. Phys. E: Sci. Instrum. 20, 217–224.CrossRefGoogle Scholar
25. Walker, J. D. A., Smith, C. R., Cerra, A. W. & Doligalski, T. L. 1987 The impact of a vortex ring on a wall. J. Fluid Mech. 181, 99–140.CrossRefGoogle Scholar
26. Westerweel, J., Dabiri, D. & Gharib, M. 1997 The effect of a discrete window offset on the accuracy of cross-correlation analysis of digital PIV recordings. Exp. Fluids 23, 20–28.CrossRefGoogle Scholar
27. Willert, C. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10, 181–193.Google Scholar
28. Yamada, H., Kohsaka, T. & Yamabe, H. 1982 Flowfield produced by a vortex ring near a plane wall. J. Phys. Soc. Japan 51, 1663–1670.Google Scholar
29. Yamada, H., Mochizuki, O. & Yamabe, H. 1985 Pressure variation on a flat wall induced by an approaching vortex ring. J. Phys. Soc. Japan 54, 4151–4160.CrossRefGoogle Scholar