Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T01:28:42.917Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction of two tandem deformable bodies in a viscous incompressible flow

Published online by Cambridge University Press:  25 August 2009

LUODING ZHU
LUODING ZHU*
Affiliation:
Department of Mathematical Sciences, Indiana University–Purdue University Indianapolis, 402 North Blackford Street, Indianapolis, IN 46202, USA
*
†Email address for correspondence: lzhu@math.iupui.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Previous laboratory measurements on drag of tandem rigid bodies moving in viscous incompressible fluids found that a following body experienced less drag than a leading one. Very recently a laboratory experiment (Ristroph & Zhang, Phys. Rev. Lett., vol. 101, 2008) with deformable bodies (rubble threads) revealed just the opposite – the leading body had less drag than the following one. The Reynolds numbers in the experiment were around 104. To find out how this qualitatively different phenomenon may depend on the Reynolds number, a series of numerical simulations are designed and performed on the interaction of a pair of tandem flexible flags separated by a dimensionless vertical distance (0 ≤ D ≤ 5.5) in a flowing viscous incompressible fluid at lower Reynolds numbers (40 ≤ Re ≤ 220) using the immersed boundary (IB) method. The dimensionless bending rigidity 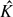b and dimensionless flag mass density 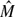used in our work are as follows: 8.6 × 10−5 ≤ 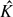b ≤ 1.8 × 10−3, 0.8 ≤ 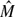≤ 1.0. We obtain an interesting result within these ranges of dimensionless parameters: when Re is large enough so that the flapping of the two flags is self-sustained, the leading flag has less drag than the following one; when Re is small enough so that the flags maintain two nearly static line segments aligned with the mainstream flow, the following flag has less drag than the leading one. The transitional range of Re separating the two differing phenomena depends on the value of 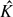b. With Re in this range, both the flapping and static states are observed depending on the separation distance D. When D is small enough, the flags are in the static state and the following flag has less drag; when D is large enough the flags are in the constant flapping state and the leading flag has less drag. The critical value of D depends on 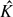b.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 635 , 25 September 2009 , pp. 455 - 475
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alben, S., Shelley, M. & Zhang, J. 2002 Drag reduction through self-similar bending of a flexible body. Nature 420, 479–481.CrossRefGoogle ScholarPubMed
Argentina, M. & Mahadevan, L. 2005 Fluid-flow induced flutter of a flag. PNAS 102, 1829.CrossRefGoogle ScholarPubMed
Atzberger, P. J., Kramer, P. R. & Peskin, C. S. 2006 A stochastic immersed boundary method for biological fluid dynamics at microscopic length scale. J. Comput. Phys. 224 (2), 1255–1292.CrossRefGoogle Scholar
Bell, J. B., Colella, P. & Glaz, H. M. 1989 A second order projection method for the incompressible Navier–Stokes equations. J. Comput. Phys. 85, 257.CrossRefGoogle Scholar
Bell, J. B., Colella, P. & Howell, L. H. 1991 An efficient second-order projection method for viscous incompressible flow. In Proceedings of the Tenth AIAA Computational Fluid Dynamics Conference, Honolulu, June 24–26 (USA).CrossRefGoogle Scholar
Bill, R. G. & Herrnkind, W. F. 1973 Drag reduction by formation movement in spiny lobsters. Science 193, 1146–1148.CrossRefGoogle Scholar
Borazjani, I., Ge, L. & Sotiropoulos, F. 2008 Curvilinear immersed boundary method for simulating fluid structure interaction with complex three-dimensional rigid bodies. J. Comput. Phys. 227 (16), 7587–7620.CrossRefGoogle Scholar
Botella, O. 1997 On the solution of the Navier–Stokes equations using Chebyshev projection schemes with third-order accuracy in time. Comput. Fluids 26, 107.CrossRefGoogle Scholar
Brown, D. L., Cortez, R. & Minion, M. L. 2001 Accurate projection methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 168 (2), 464.CrossRefGoogle Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Math. Comput. 22, 745.CrossRefGoogle Scholar
Chorin, A. J. 1969 On the convergence of discrete approximations to the Navier–Stokes equations. Math. Comput. 23, 341.CrossRefGoogle Scholar
Connell, B. S. H. & Yue, D. K. P. 2007 Flapping dynamics of a flag in a uniform stream. J. Fluid Mech. 581, 33–67.CrossRefGoogle Scholar
Cottet, G. H. & Maitre, E. 2004 A level set formulation of immersed boundary methods for fluid-structure interaction problems. C. R. Acad. Sci. Paris, Ser. I 338, 581–586.CrossRefGoogle Scholar
Cottet, G. H. & Maitre, E. 2006 A level set method for fluid-structure interactions with immersed interfaces. Math. Models Methods Applied Sci. 16, 415–438.CrossRefGoogle Scholar
Donea, J. Giuliani, S. & Halleux, J. P. 1982 An arbitrary Lagrangian–Eulerian finite element method for transient dynamic fluid structure interactions. Comput. Methods Appl. Mech. Engng 33, 689.CrossRefGoogle Scholar
Dong, G.-J. & Lu, X.-Y. 2007 Characteristics of flow over travelling wavy foils in a side-by-side arrangement. Phys. Fluids 19, 057107.CrossRefGoogle Scholar
Farnell, D. J. J., David, T. & Barton, D. C. 2004 Coupled states of flapping flags J. Fluids Struct. 19, 29–36.CrossRefGoogle Scholar
Fauci, L. J. 1990 Interaction of oscillating filaments: a computational study. J. Comput. Phys. 86, 294–313.CrossRefGoogle Scholar
Fauci, L. J. & Fogelson, A. L. 1993 Truncated Newton methods and the modelling of complex elastic structures. Commun. Pure Appl. Math. 46, 787.CrossRefGoogle Scholar
Fauci, L. & Peskin, C. S. 1988 A computational model of aquatic animal locomotion. J. Comput. Phys. 77, 85–108.CrossRefGoogle Scholar
Fedkiw, R. P. 2002 Coupling an Eulerian fluid calculation to a Lagrangian solid calculation with the ghost fluid method. J. Comput. Phys. 175 (1), 200–224.CrossRefGoogle Scholar
Fedkiw, R. P., Aslam, T., Merriman, B. & Osher, S. 1999 A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method). J. Comput. Phys. 152 (2), 457–492.CrossRefGoogle Scholar
Fogelson, A. L. & Peskin, C. S. 1988 A fast numerical method for solving the three-dimensional Stokes' equations in the presence of suspended particles. J. Comput. Phys. 79, 50–69.CrossRefGoogle Scholar
Glowinski, R., Pan, T., Hesla, T., Joseph, D. & Periaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 169, 363.CrossRefGoogle Scholar
Glowinski, R., Pan, T. & Periaux, J. 1994 a A fictitious domain method for Dirichlet problem and applications. Comput. Methods Appl. Mech. Engng 111.CrossRefGoogle Scholar
Glowinski, R., Pan, T. & Periaux, J. 1994 b A fictitious domain method for external incompressible viscous flow modelled by Navier–Stokes equations. Comput. Methods Appl. Mech. Engng 112.CrossRefGoogle Scholar
Griffith, B. E. & Peskin, C. S. 2005 On the order of accuracy of the immersed boundary method: higher order convergence rates for sufficient smooth problems. J. Comput. Phys. 208 (1), 75–105.CrossRefGoogle Scholar
Hou, T. Y., Li, Z. L., Osher, S. & Zhao, H. K. 1997 A hybrid method for moving interface problems with application to the Hele–Shaw flow. J. Comput. Phys. 134, 236–252.CrossRefGoogle Scholar
Hughes, T. J. R., Liu, W. & Zimmerman, T. K. 1981 Lagrangian–Eulerian finite element formulation for incompressible viscous flows. Comput. Methods Appl. Mech. Engng 29.CrossRefGoogle Scholar
Jia, L. B., Li, F., Yin, X. Z. & Yin, , 2007 Coupling modes between two flapping filaments. J. Fluid Mech. 581, 199–220.CrossRefGoogle Scholar
Kim, Y. & Peskin, C. S. 2007 Penalty immersed boundary method for an elastic boundary with mass. Phys. Fluids 19 (5), 053103.CrossRefGoogle Scholar
Kyle, C. R. 1979 Reduction of wind resistance and power output of racing cyclists and runners travelling in groups. Ergonomics 22, 387–397.CrossRefGoogle Scholar
Lai, M. C. & Peskin, C. S. 2000 An immersed boundary method with formal second order accuracy and reduced numerical viscosity. J. Comput. Phys. 160, 705.CrossRefGoogle Scholar
LeVeque, R. J. & Li, Z. L. 1994 The immersed interface method for elliptic equations with discontinuous coefficients and singular sources. SIAM J. Numer. Anal. 31, 1019–1044.CrossRefGoogle Scholar
LeVeque, R. J. & Li, Z. L. 1997 Immersed interface methods for Stokes flows with elastic boundaries or surface tension. SIAM J. Sci. Comput. 18, 709–735.CrossRefGoogle Scholar
Li, Z. L. 2006 The Immersed Interface Method – Numerical Solutions of PDEs Involving Interfaces and Irregular Domains. SIAM.Google Scholar
Li, Z. L. & Lai, M. C. 2001 Immersed interface methods for Navier–Stokes equations with singular forces. J. Comput. Phys. 171, 822–842.CrossRefGoogle Scholar
Liao, J. C., Beal, D. N., Lauder, G. V. & Triantafyllou, M. S. 2003 The Kármán gait: novel body kinematics of rainbow trout swimming in a vortex street. J. Exp. Biol. 206, 1059.CrossRefGoogle Scholar
Liu, W. K., Kim, D. K. & Tang, S. 2006 Mathematical foundations of the immersed finite element method. Comput. Mech., 39 (3), 211–222.CrossRefGoogle Scholar
Lopez, J. M., Marques, F. & Shen, J. 2002 An efficient spectral-projection method for the Navier–Stokes equations in cylindrical geometries II. Three-dimensional cases. J. Comput. Phys. 176 (2), 384–401.CrossRefGoogle Scholar
Lopez, J. M. & Shen, J. 1998 An efficient spectral-projection method for the Navier–Stokes equations in cylindrical geometries I. Axisymmetric cases. J. Comput. Phys. 139 (2), 308–326.CrossRefGoogle Scholar
Mittal, R. & Iaccarino, G. 2005 Immersed boundary methods. Annu. Rev. Fluid Mech. 37, 239–261.CrossRefGoogle Scholar
Mori, Y. & Peskin, C. S. 2008 Implicit second-order immersed boundary method with boundary mass. Comput. Methods Appl. Mech. Eng. 197, 1213–1263.CrossRefGoogle Scholar
Perot, J. B. 1993 An analysis of the fractional step method. J. Comput. Phys. 108, 51.CrossRefGoogle Scholar
Peskin, C. S. 1977 Flow patterns around heart valves: a numerical method. J. Comput. Phys. 25, 220.CrossRefGoogle Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479.CrossRefGoogle Scholar
Peskin, C. S. & McQueen, D. M. 1993 Computational biofluid dynamics. Contemp. Math. 141, 161.CrossRefGoogle Scholar
Qi, D. & Shyy, W. Submitted Simulations of dynamics of free falling of flexible fibres in moderate Reynolds number flows. J. Fluid Mech.Google Scholar
Ristroph, L. & Zhang, J. 2008 Anomalous hydrodynamic drafting of interacting flapping flags. Phys. Rev. Lett. 101, 194502.CrossRefGoogle ScholarPubMed
Roma, A. M., Peskin, C. S. & Berger, M. J. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153, 509–534.CrossRefGoogle Scholar
Romberg, C. F., Chianese, Jr., F. & Lajoie, R. G. 1971 Aerodynamics of race cars in drafting and passing situations. Soc. Auto. Engng 710213.CrossRefGoogle Scholar
Sheldon Wang, X. 2007 An iterative matrix-free method in implicit immersed boundary/continuum methods. Comput. Struct. 85, 739–748.CrossRefGoogle Scholar
Shelley, M., Vandenberghe, N. & Zhang, J. 2005 Heavy flags undergo spontaneous oscillations in flowing water. Phys. Rev. Lett. 94 (9), 094302.CrossRefGoogle ScholarPubMed
Sulsky, D., Chen, Z. & Schreyer, H. L. 1994 a A particle method for history-dependent materials. Comput. Mech. Appl. Mech. Engng 118, 179–197.CrossRefGoogle Scholar
Sulsky, D., Zhou, S. J. & Schreyer, H. L. 1994 b Application of a particle-in-cell method to solid mechanics. Comput. Phys. Commun. 87, 136–152.Google Scholar
Wang, X. 2006 From immersed boundary method to immersed continuum method. Intl J. Multiscale Comput. Engng 4 (1), 127–145.CrossRefGoogle Scholar
Wang, X. & Liu, W. K. 2004 Extended immersed boundary method using FEM and RKPM. Comput. Methods Appl. Mech. Engng, 193 (12–14), 1305.CrossRefGoogle Scholar
Weinan, E. & Liu, J.-G. 1995 Projection method I: convergence and numerical boundary layers. SIAM J. Numer. Anal. 32, 1017.Google Scholar
Weinan, E. & Liu, J.-G. 1996 Projection method II: Godunov–Ryabenki analysis. SIAM J. Numer. Anal. 33, 1597.Google Scholar
Williams, H. A. R., Fauci, L. J. & Gaver, D. P. 2009 Evaluation of interfacial fluid dynamical stresses using the immersed boundary method. Discrete Continuous Dyn. Syst., Ser. B 11 (2), 519–540.CrossRefGoogle ScholarPubMed
Xu, J., Li, Z., Lowengrub, J. & Zhao, H. 2006 A level set method for interfacial flows with surfactant. J. Comput. Phys. 212 (2), 590–616.CrossRefGoogle Scholar
Zdravkovich, M. M. 1977 Review of flow interference between two circular cylinders in various arrangement. J. Fluids Engng 99, 618–633.CrossRefGoogle Scholar
Zhang, J., Childress, S. Libchaber, A. & Shelley, M. 2000 Flexible filaments in a flowing soap film as a model for one-dimensional flags in a two-dimensional wind. Nature 408, 835.CrossRefGoogle Scholar
Zhang, L., Gersternberger, A., Wang, X. & Liu, W. K. 2004 Immersed finite element method. Comput. Methods Appl. Mech. Engng 193, 2051.CrossRefGoogle Scholar
Zhu, L. 2008 Scaling law for drag of a flexible object moving in an incompressible viscous fluid. J. Fluid Mech. 607, 387–400.CrossRefGoogle Scholar
Zhu, L. & Chin, R. 2008 Simulation of elastic filaments interacting with a viscous pulsatile flow. Comput. Method Appl. Mech. Engng 197, 2265–2274.CrossRefGoogle Scholar
Zhu, L. & Peskin, C. S. 2002 Simulation of a flexible flapping filament in a flowing soap film by the immersed boundary method. J. Comput. Phys. 179 (2), 452–468.CrossRefGoogle Scholar
Zhu, L. & Peskin, C. S. 2003 Interaction of two flexible filaments in a flowing soap film. Phys. Fluids 15 (7), 1954–1960.CrossRefGoogle Scholar