Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Khusnutdinova, Karima R.
and
Pelinovsky, Dmitry E.
2019.
Preface: Nonlinear waves in fluids in honor of Roger Grimshaw on the occasion of his 80th birthday.
Studies in Applied Mathematics,
Vol. 142,
Issue. 3,
p.
215.
Liu, Zihua
Grimshaw, Roger
and
Johnson, Edward
2019.
Generation of mode 2 internal waves by the interaction of mode 1 waves with topography.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
799.
Lai, Zhigang
Jin, Guangzhen
Huang, Yongmao
Chen, Haiyun
Shang, Xiaodong
and
Xiong, Xuejun
2019.
The Generation of Nonlinear Internal Waves in the South China Sea: A Three‐Dimensional, Nonhydrostatic Numerical Study.
Journal of Geophysical Research: Oceans,
Vol. 124,
Issue. 12,
p.
8949.
Lan, Zhongzhou
2019.
Periodic, breather and rogue wave solutions for a generalized (3+1)-dimensional variable-coefficient B-type Kadomtsev–Petviashvili equation in fluid dynamics.
Applied Mathematics Letters,
Vol. 94,
Issue. ,
p.
126.
Grimshaw, Roger H. J.
and
Maleewong, Montri
2019.
Transcritical flow over obstacles and holes: forced Korteweg–de Vries framework.
Journal of Fluid Mechanics,
Vol. 881,
Issue. ,
p.
660.
Du, Hui
Wei, Gang
Wang, Shao-Dong
and
Wang, Xin-Long
2019.
Experimental study of elevation- and depression-type internal solitary waves generated by gravity collapse.
Physics of Fluids,
Vol. 31,
Issue. 10,
Maleewong, Montri
and
Grimshaw, Roger H. J.
2020.
Transcritical flow over obstacles and holes: Forced extended Korteweg–de Vries framework.
Physical Review Fluids,
Vol. 5,
Issue. 5,
Nik Ismail, Nik Nur Amiza
Alias, Azwani
and
Harun, Fatimah N.
2020.
The Propagation of Nonlinear Internal Waves under the Influence of Variable Topography and Earth’s Rotation in a Two-Layer Fluid.
Fluids,
Vol. 5,
Issue. 3,
p.
140.
Yuan, C.
Wang, Z.
and
Chen, X.
2020.
The derivation of an isotropic model for internal waves and its application to wave generation.
Ocean Modelling,
Vol. 153,
Issue. ,
p.
101663.
Yuan, C.
Grimshaw, R.
Johnson, E.
and
Whitfield, A.
2020.
Generation of nonlinear internal waves by flow over topography: Rotational effects.
Physical Review E,
Vol. 101,
Issue. 3,
Jia, Tong
Liang, Jianjun
Li, Qiang
Sha, Jin
and
Li, Xiao‐Ming
2021.
Generation of Shoreward Nonlinear Internal Waves South of the Hainan Island: Synthetic Aperture Radar Observations and Numerical Simulations.
Journal of Geophysical Research: Oceans,
Vol. 126,
Issue. 6,
Zhang, Peiwen
Li, Qun
Xu, Zhenhua
and
Yin, Baoshu
2022.
Internal solitary wave generation by the tidal flows beneath ice keel in the Arctic Ocean.
Journal of Oceanology and Limnology,
Vol. 40,
Issue. 3,
p.
831.
Liu, Z.
Zhang, W. G.
and
Helfrich, K. R.
2022.
Vertical Structure of Barotropic‐to‐Baroclinic Tidal Energy Conversion on a Continental Slope.
Journal of Geophysical Research: Oceans,
Vol. 127,
Issue. 9,
Mistri, Arindam
Chakraborty, Debkumar
and
Ghosh, Samiran
2023.
Nonlinear coherent structures of electrostatic ion cyclotron wave induced by a moving obstacle.
Physics of Fluids,
Vol. 35,
Issue. 7,
Zhao, Binbin
Zhang, Tianyu
Duan, Wenyang
Wang, Zhan
Guo, Xinyu
Hayatdavoodi, Masoud
and
Ertekin, R. Cengiz
2023.
Internal solitary waves generated by a moving bottom disturbance.
Journal of Fluid Mechanics,
Vol. 963,
Issue. ,
Xuan, Pu
Du, Hui
Wang, Shaodong
Peng, Pai
and
Wei, Gang
2024.
The applicability of nonlinear theories of the internal solitary wave and its loads on slender body by experimental methods.
Applied Ocean Research,
Vol. 153,
Issue. ,
p.
104279.
Mistri, Arindam
Biswas, Akash
and
Ghosh, Samiran
2025.
Weakly nonlinear dynamics of magnetosonic wave at a critical angle excited by a moving charged object in collisional plasmas.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 481,
Issue. 2306,
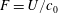 $F=U/c_{0}$, where
$F=U/c_{0}$, where 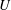 $U$ is the tidal flow amplitude and
$U$ is the tidal flow amplitude and 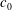 $c_{0}$ is the intrinsic linear long wave phase speed, that is the speed in the absence of the tidal current. For steady tidal flow in the resonant regime,
$c_{0}$ is the intrinsic linear long wave phase speed, that is the speed in the absence of the tidal current. For steady tidal flow in the resonant regime, 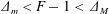 $\unicode[STIX]{x1D6E5}_{m}<F-1<\unicode[STIX]{x1D6E5}_{M}$, a theory based on the forced Korteweg–de Vries equation shows that upstream and downstream propagating undular bores are produced. The bandwidth limits
$\unicode[STIX]{x1D6E5}_{m}<F-1<\unicode[STIX]{x1D6E5}_{M}$, a theory based on the forced Korteweg–de Vries equation shows that upstream and downstream propagating undular bores are produced. The bandwidth limits 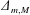 $\unicode[STIX]{x1D6E5}_{m,M}$ depend on the height (or depth) of the topographic forcing term, which can be either positive or negative depending on whether the topography is equivalent to a hole or a sill. Here the wave generation process is studied numerically using a forced Korteweg–de Vries equation model with time-dependent Froude number,
$\unicode[STIX]{x1D6E5}_{m,M}$ depend on the height (or depth) of the topographic forcing term, which can be either positive or negative depending on whether the topography is equivalent to a hole or a sill. Here the wave generation process is studied numerically using a forced Korteweg–de Vries equation model with time-dependent Froude number, 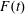 $F(t)$, representative of realistic tidal flow. The response depends on
$F(t)$, representative of realistic tidal flow. The response depends on 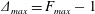 $\unicode[STIX]{x1D6E5}_{max}=F_{max}-1$, where
$\unicode[STIX]{x1D6E5}_{max}=F_{max}-1$, where 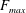 $F_{max}$ is the maximum of
$F_{max}$ is the maximum of 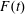 $F(t)$ over half of a tidal cycle. When
$F(t)$ over half of a tidal cycle. When 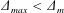 $\unicode[STIX]{x1D6E5}_{max}<\unicode[STIX]{x1D6E5}_{m}$ the flow is always subcritical and internal solitary waves appear after release of the downstream disturbance. When
$\unicode[STIX]{x1D6E5}_{max}<\unicode[STIX]{x1D6E5}_{m}$ the flow is always subcritical and internal solitary waves appear after release of the downstream disturbance. When 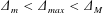 $\unicode[STIX]{x1D6E5}_{m}<\unicode[STIX]{x1D6E5}_{max}<\unicode[STIX]{x1D6E5}_{M}$ the flow reaches criticality at its peak, producing upstream and downstream undular bores that are released as the tide slackens. When
$\unicode[STIX]{x1D6E5}_{m}<\unicode[STIX]{x1D6E5}_{max}<\unicode[STIX]{x1D6E5}_{M}$ the flow reaches criticality at its peak, producing upstream and downstream undular bores that are released as the tide slackens. When 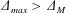 $\unicode[STIX]{x1D6E5}_{max}>\unicode[STIX]{x1D6E5}_{M}$ the tidal flow goes through the resonant regime twice, producing undular bores with each passage. The numerical simulations are for both symmetrical topography, and for asymmetric topography representative of Stellwagen Bank and Knight Inlet.
$\unicode[STIX]{x1D6E5}_{max}>\unicode[STIX]{x1D6E5}_{M}$ the tidal flow goes through the resonant regime twice, producing undular bores with each passage. The numerical simulations are for both symmetrical topography, and for asymmetric topography representative of Stellwagen Bank and Knight Inlet.