Article contents
The internal wavefield generated by a towed sphere at low Froude number
Published online by Cambridge University Press: 13 March 2015
Abstract
In highly stratified atmospheric and oceanic environments, a large fraction of energy input by various sources can be manifest as internal waves (IWs). The propagating nature of IWs results in the distribution of the energy over a large fraction of the air/water column. Wakes of translating bodies are one source of input energy that has been of continued interest. To further the understanding of wakes in strongly stratified environments, and particularly the near-field regime where strong coupling to the internal wavefield is evident, an extensive series of experiments on the internal wavefield generated by a towed sphere was performed, wherein the internal wavefield was measured over a Froude number range 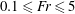 $0.1\leqslant \mathit{Fr}\leqslant 5$ (where
$0.1\leqslant \mathit{Fr}\leqslant 5$ (where 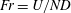 $\mathit{Fr}=U/ND$,
$\mathit{Fr}=U/ND$, 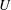 $U$ is the tow speed,
$U$ is the tow speed, 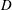 $D$ the sphere diameter and
$D$ the sphere diameter and 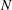 $N$ the Brunt–Väisälä (BV) frequency). In a second series of experiments, the temporal wavefield evolution was studied over two BV periods. These measurements show that the body generation (lee wave) mechanism dominates at
$N$ the Brunt–Väisälä (BV) frequency). In a second series of experiments, the temporal wavefield evolution was studied over two BV periods. These measurements show that the body generation (lee wave) mechanism dominates at 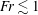 $\mathit{Fr}\lesssim 1$, while the random eddies in the turbulent wake become the dominant source at
$\mathit{Fr}\lesssim 1$, while the random eddies in the turbulent wake become the dominant source at 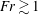 $\mathit{Fr}\gtrsim 1$. In the low-
$\mathit{Fr}\gtrsim 1$. In the low-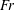 $\mathit{Fr}$ regime,
$\mathit{Fr}$ regime, 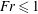 $\mathit{Fr}\leqslant 1$, there is a resonant peak in the coupling of the input wake energy to the internal wavefield at a Froude number of
$\mathit{Fr}\leqslant 1$, there is a resonant peak in the coupling of the input wake energy to the internal wavefield at a Froude number of 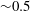 ${\sim}0.5$, and at its maximum 70 % of the input energy is coupled into IW potential energy. In this regime it was also found that the spreading angle of the evolving wavefield was considerably broader than predicted by the classical point-source models for the wavefield further downstream, owing to the existence in the near field of a significant energy content in the higher-IW modes that deteriorate at later times. In the low-
${\sim}0.5$, and at its maximum 70 % of the input energy is coupled into IW potential energy. In this regime it was also found that the spreading angle of the evolving wavefield was considerably broader than predicted by the classical point-source models for the wavefield further downstream, owing to the existence in the near field of a significant energy content in the higher-IW modes that deteriorate at later times. In the low-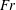 $\mathit{Fr}$ regime, it was found that, while the IW potential energy increases
$\mathit{Fr}$ regime, it was found that, while the IW potential energy increases 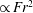 $\propto \mathit{Fr}^{2}$, the fraction of the total energy input is a weak function of
$\propto \mathit{Fr}^{2}$, the fraction of the total energy input is a weak function of 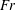 $\mathit{Fr}$, varying as
$\mathit{Fr}$, varying as 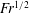 $\mathit{Fr}^{1/2}$.
$\mathit{Fr}^{1/2}$.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 24
- Cited by



