Article contents
Investigations on the turbulent ${\boldsymbol{/}}$non-turbulent interface in supersonic compressible plate turbulent boundary layer
${\boldsymbol{/}}$non-turbulent interface in supersonic compressible plate turbulent boundary layer
Published online by Cambridge University Press: 03 June 2024
Abstract
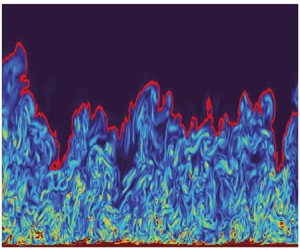
The turbulent boundary layer (TBL) is a widely existing flow phenomenon in nature and engineering applications. Its strong mixing effect can achieve more sufficient material mixing, heat transport, etc. The understanding of the entrainment process and mechanism of irrotational fluids entering the turbulent region can be promoted by studying the geometric and dynamic characteristics of turbulent ${/}$non-turbulent interfaces (TNTI). In compressible flow, it is unclear whether the properties of TNTI will change and whether the entrainment will show different features due to the influence of compressibility. Based on the direct numerical simulation results of supersonic compressible plate TBLs with Mach number of 2.9, the geometric and dynamic characteristics of TNTI are investigated in this paper. The interface is identified by the enstrophy method, and the height, thickness, fractal dimension, enstrophy transportation and entrainment characteristics of the interface are investigated. It is found that for the enstrophy transportation in a TBL, the contribution of compressibility-related terms accounts for approximately 13.4 % of the total enstrophy transportation, which tends to transfer the enstrophy of turbulence near the interface to both directions vertical to the interface. This promotes the expansion of the turbulent region towards the non-turbulent region, and the mean height, thickness and entrainment velocity are increased by approximately 3.7 %, 7.0 % and 8.5 %, respectively, while the fractal dimension is basically unaffected. Different from the incompressible flow, the contribution of the compressibility-related terms to the entrainment velocity is independent of the local curvature, and the intense entrainment process is more likely to occur on a highly curved concave surface.
${/}$non-turbulent interfaces (TNTI). In compressible flow, it is unclear whether the properties of TNTI will change and whether the entrainment will show different features due to the influence of compressibility. Based on the direct numerical simulation results of supersonic compressible plate TBLs with Mach number of 2.9, the geometric and dynamic characteristics of TNTI are investigated in this paper. The interface is identified by the enstrophy method, and the height, thickness, fractal dimension, enstrophy transportation and entrainment characteristics of the interface are investigated. It is found that for the enstrophy transportation in a TBL, the contribution of compressibility-related terms accounts for approximately 13.4 % of the total enstrophy transportation, which tends to transfer the enstrophy of turbulence near the interface to both directions vertical to the interface. This promotes the expansion of the turbulent region towards the non-turbulent region, and the mean height, thickness and entrainment velocity are increased by approximately 3.7 %, 7.0 % and 8.5 %, respectively, while the fractal dimension is basically unaffected. Different from the incompressible flow, the contribution of the compressibility-related terms to the entrainment velocity is independent of the local curvature, and the intense entrainment process is more likely to occur on a highly curved concave surface.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 7
- Cited by


