Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T06:46:32.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Isotropization at small scales of rotating helically driven turbulence

Published online by Cambridge University Press:  13 April 2012

P. D. Mininni ,
D. Rosenberg  and
A. Pouquet
P. D. Mininni
Affiliation:
National Center for Atmospheric Research, PO Box 3000, Boulder, CO 80307, USA
D. Rosenberg
Affiliation:
National Center for Atmospheric Research, PO Box 3000, Boulder, CO 80307, USA
A. Pouquet*
Affiliation:
National Center for Atmospheric Research, PO Box 3000, Boulder, CO 80307, USA
*
†Email address for correspondence: pouquet@ucar.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

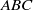We present numerical evidence of how three-dimensionalization occurs at small scale in rotating turbulence with Beltrami () forcing, creating helical flow. The Zeman scale 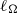at which the inertial and eddy turn-over times are equal is more than one order of magnitude larger than the dissipation scale, with the relevant domains (large-scale inverse cascade of energy, dual regime in the direct cascade of energy 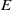and helicity 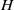, and dissipation) each moderately resolved. These results stem from the analysis of a large direct numerical simulation on a grid of 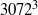points, with Rossby and Reynolds numbers, respectively, equal to 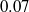and 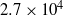. At scales smaller than the forcing, a helical wave-modulated inertial law for the energy and helicity spectra is followed beyond 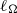by Kolmogorov spectra for 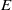and 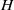. Looking at the two-dimensional slow manifold, we also show that the helicity spectrum breaks down at 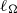, a clear sign of recovery of three-dimensionality in the small scales.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Rotating turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 699 , 25 May 2012 , pp. 263 - 279
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Also at Departamento de Fí sica, Facultad de Ciencias Exactas y Naturales and IFIBA, CONICET, Ciudad Universitaria, 1428 Buenos Aires, Argentina.

References

1. Archontis, V., Dorch, S. B. F. & Nordlund, Å. 2003 Dynamo action in turbulent flows. Astron. Astrophys. 410, 759–766.CrossRefGoogle Scholar
2. Baerenzung, J., Rosenberg, D., Mininni, P. D. & Pouquet, A. 2011 Helical turbulence prevails over inertial waves in forced rotating flows at high Reynolds and low Rossby numbers. J. Atmos. Sci. 68, 2757–2770.CrossRefGoogle Scholar
3. Baroud, C. N., Plapp, B. B., Swinney, H. L & She, Z.-S. 2003 Scaling in three-dimensional and quasi-two-dimensional rotating turbulent flows. Phys. Fluids 15, 2091–2104.CrossRefGoogle Scholar
4. Bartello, P., Métais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273, 1–29.CrossRefGoogle Scholar
5. Bellet, F., Godeferd, F. S., Scott, F. S. & Cambon, C. 2006 Wave turbulence in rapidly rotating flows. J. Fluid Mech. 562, 83–121.CrossRefGoogle Scholar
6. van Bokhoven, L. J., Clercx, H. J. H., van Heijst, G. J. F. & Trieling, R. R. 2009 Experiments on rapidly rotating turbulent flows. Phys. Fluids 21, 096601.CrossRefGoogle Scholar
7. Bourouiba, L. & Bartello, P. 2007 The intermediate Rossby number range and two-dimensional–three-dimensional transfers in rotating decaying homogeneous turbulence. J. Fluid Mech. 587, 139–161.CrossRefGoogle Scholar
8. Brissaud, A., Frisch, U., Léorat, J., Lesieur, M. & Mazure, A. 1973 Helicity cascades in fully developed isotropic turbulence. J. Fluid Mech. 202, 295–317.Google Scholar
9. Cambon, C. & Jacquin, L. 1989 Spectral approach to non isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.CrossRefGoogle Scholar
10. Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.CrossRefGoogle Scholar
11. Cambon, C., Rubinstein, R. & Godeferd, F. S. 2004 Advances in wave turbulence: rapidly rotating flows. New J. Phys. 6, 73.CrossRefGoogle Scholar
12. Cambon, C. & Scott, J. F. 1999 Linear and nonlinear models of anisotropic turbulence. Annu. Rev. Fluid Mech. 11, 1–53.CrossRefGoogle Scholar
13. Canuto, V. M. & Dubovikov, M. S. 1997 A dynamical model for turbulence. V. The effect of rotation. Phys. Fluids 9, 2132–2140.CrossRefGoogle Scholar
14. Chakraborty, S. 2007 Signatures of two-dimensionalization of 3D turbulence in the presence of rotation. Eur. Phys. Lett. 79, 14002.CrossRefGoogle Scholar
15. Chakraborty, S. & Batthacharjee, J. K. 2007 Third-order structure function for rotating in three-dimensional homogeneous turbulent flow. Phys. Rev. E 76, 036304.CrossRefGoogle ScholarPubMed
16. Chen, Q., Chen, S. & Eyink, G. 2003 The joint cascade of energy and helicity in three-dimensional turbulence. Phys. Fluids 15, 361–374.CrossRefGoogle Scholar
17. Chen, Q., Chen, S., Eyink, G. L. & Holm, D. D. 2005 Resonant interactions in rotating homogeneous three-dimensional turbulence. J. Fluid Mech. 542, 139–164.CrossRefGoogle Scholar
18. Davidson, P. A., Staplehurst, P. J. & Dalziel, S. B. 2006 On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 557, 135–144.CrossRefGoogle Scholar
19. Dubrulle, B. & Valdetarro, L. 1992 Consequences of rotation in energetics of accretion disks. Astron. Astrophys. 263, 387–400.Google Scholar
20. Galtier, S. 2003 Weak inertial-wave turbulence theory. Phys. Rev. E 68, 015301(R).CrossRefGoogle ScholarPubMed
21. Gómez, D. O, Mininni, P. D. & Dmitruk, P. 2005 Parallel simulations in turbulent MHD. Phys. Scr. 116, 123–127.CrossRefGoogle Scholar
22. Hopfinger, E. J., Browand, F. K. & Gagne, Y. 1982 Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534.CrossRefGoogle Scholar
23. Hopfinger, E. J. & van Heijst, G. J. 1993 Vortices in rotating fluids. Annu. Rev. Fluid Mech. 25, 241–289.CrossRefGoogle Scholar
24. Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
25. Koprov, B. M., Koprov, V. M., Ponomarev, V. M. & Chkhetiani, O. G. 2005 Experimental studies of turbulent helicity and its spectrum in the atmospheric boundary layer. Dokl. Phys. 50, 419–422 (translation in 2005 Dokl. Akad. Nauk 403, 627–630).CrossRefGoogle Scholar
26. Kraichnan, R. H. 1973 Helical turbulence and absolute equilibrium. J. Fluid Mech. 59, 745–752.CrossRefGoogle Scholar
27. Lamriben, C., Cortet, P.-P. & Moisy, F. 2011 Direct measurements of anisotropic energy transfers in a rotating turbulent experiment. Phys. Rev. Lett. 107, 024503.CrossRefGoogle Scholar
28. Lilly, D. 1986 The structure, energetics and propagation of rotating convective storms. Part II: Helicity and storm stabilization. J. Atmos. Sci. 43, 126–140.2.0.CO;2>CrossRefGoogle Scholar
29. Matthaeus, W. H., Pouquet, A., Mininni, P. D., Dmitruk, P. & Breech, B. 2008 Rapid directional alignment of velocity and magnetic field in magnetohydrodynamic turbulence. Phys. Rev. Lett. 100, 085003.CrossRefGoogle ScholarPubMed
30. Mininni, P. D., Alexakis, A. & Pouquet, A. 2008 Non-local interactions in hydrodynamic turbulence at high Reynolds numbers: the slow emergence of scaling laws. Phys. Rev. E 77, 036306.CrossRefGoogle Scholar
31. Mininni, P. D., Alexakis, A. & Pouquet, A. 2009 Scale interactions and scaling laws in rotating flows at moderate Rossby numbers and large Reynolds numbers. Phys. Fluids 21, 015108.CrossRefGoogle Scholar
32. Mininni, P. D. & Pouquet, A. 2009 Helicity cascades in rotating turbulence. Phys. Rev. E 79, 026304.CrossRefGoogle ScholarPubMed
33. Mininni, P. D. & Pouquet, A. 2010a Rotating helical turbulence. Part I. Global evolution and spectral behaviour. Phys. Fluids 22, 035105.CrossRefGoogle Scholar
34. Mininni, P. D. & Pouquet, A. 2010b Rotating helical turbulence. Part II. Intermittency, scale invariance and structures. Phys. Fluids 22, 035106.CrossRefGoogle Scholar
35. Mininni, P. D., Rosenberg, D., Reddy, R. & Pouquet, A. 2011 A hybrid MPI–OpenMP scheme for scalable parallel pseudospectral computations for fluid turbulence. Parallel Comput. 37, 316–326.CrossRefGoogle Scholar
36. Moffatt, H. K. & Tsinober, A. 1992 Helicity in laminar and turbulent flow. Annu. Rev. Fluid Mech. 24, 281–312.CrossRefGoogle Scholar
37. Moisy, F., Morize, C., Rabaud, M. & Sommeria, J. 2011 Decay laws, anisotropy and cyclone–anticyclone asymmetry in decaying rotating turbulence. J. Fluid Mech. 666, 5–35.CrossRefGoogle Scholar
38. Müller, W.-C. & Thiele, M. 2007 Scaling and energy transfer in rotating turbulence. Europhys. Lett. 77, 34003.CrossRefGoogle Scholar
39. Nazarenko, S. V. & Schekochihin, A. A. 2011 Critical balance in magnetohydrodynamic, rotating and stratified turbulence: towards a universal scaling conjecture. J. Fluid Mech. 677, 134–153.CrossRefGoogle Scholar
40. Newell, A. C. 1969 Rossby wave packet interactions. J. Fluid Mech. 35, 255–271.CrossRefGoogle Scholar
41. Orlandi, P. & Fatica, M. 1997 Direct simulations of turbulent flow in a pipe rotating about its axis. J. Fluid Mech. 343, 43–72.CrossRefGoogle Scholar
42. Plunian, F. & Stepanov, R. 2010 Cascades and dissipation ratio in rotating magnetohydrodynamic turbulence at low magnetic Prandtl number. Phys. Rev. E 82, 046311.CrossRefGoogle ScholarPubMed
43. Podvigina, O. & Pouquet, A. 1994 On the nonlinear stability of the 1:1:1 ABC flow. Physica D 75, 475–508.CrossRefGoogle Scholar
44. Pouquet, A. & Mininni, P. D. 2010 The interplay between helicity and rotation in turbulence: implications for scaling laws and small-scale dynamics. Phil. Trans. R. Soc. 368, 1635–1662.CrossRefGoogle ScholarPubMed
45. Pouquet, A. & Patterson, G. S. 1978 Numerical simulation of helical magnetohydrodynamic turbulence. J. Fluid Mech. 85, 305–323.CrossRefGoogle Scholar
46. Proudman, J. 1916 On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 92, 408–424.Google Scholar
47. Seiwert, J., Morize, C. & Moisy, F. 2008 On the decrease of intermittency in decaying rotating turbulence. Phys. Fluids 20, 071702.CrossRefGoogle Scholar
48. Simand, C. 2002 Étude de la turbulence au voisinage d’un vortex. Thèse de Doctorat de l’Université de Lyon, École Normale Supérieure de Lyon.Google Scholar
49. Smith, L., Chasnov, R. & Waleffe, F. 1996 Crossover from two- to three-dimensional turbulence. Phys. Rev. Lett. 77, 2467–2470.CrossRefGoogle ScholarPubMed
50. Smith, L. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 1608–1622.CrossRefGoogle Scholar
51. Taylor, G. I. 1917 Motion of solids in fluids when the flow is not irrotational. Proc. R. Soc. Lond. A 93, 92–113.Google Scholar
52. Teitelbaum, T. & Mininni, P. D. 2011 Effect of helicity and rotation on the free decay of turbulent flows. Phys. Rev. Lett. 103, 014501.Google Scholar
53. Waleffe, F. 1993 Inertial transfers in the helical decomposition. Phys. Fluids A 5, 677–685.CrossRefGoogle Scholar
54. Zeman, O. 1994 A note on the spectra and decay of rotating homogeneous turbulence. Phys. Fluids 6, 3221–3223.CrossRefGoogle Scholar
55. Zhou, Y. 1995 A phenomenological treatment of rotating turbulence. Phys. Fluids 7, 2092–2094.CrossRefGoogle Scholar