Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-29T02:32:25.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Jet-noise control by fluidic injection from a rotating plug: linear and nonlinear sound-source mechanisms

Published online by Cambridge University Press:  05 January 2016

Maxime Kœnig ,
Kenzo Sasaki ,
André V. G. Cavalieri ,
Peter Jordan  and
Yves Gervais
Maxime Kœnig*
Affiliation:
Acoustics Department, Safran Snecma, 77550 Moissy-Cramayel, France
Kenzo Sasaki
Affiliation:
Instituto Tecnológico de Aeronáutica, São José dos Campos 12228900, Brazil
André V. G. Cavalieri
Affiliation:
Instituto Tecnológico de Aeronáutica, São José dos Campos 12228900, Brazil
Peter Jordan
Affiliation:
Departement Fluides, Thermique, Combustion, Institut Pprime, 86036 Poitiers, France
Yves Gervais
Affiliation:
Departement Fluides, Thermique, Combustion, Institut Pprime, 86036 Poitiers, France
*
†Email address for correspondence: maxime.koenig@snecma.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a study of the turbulent and acoustic fields of subsonic jets, controlled by means of a novel actuator that introduces perturbations via steady-fluidic actuation from a rotating centrebody. The actuation can produce louder or quieter jets, and these are analysed using time-resolved stereoscopic particle image velocimetry and a hot-wire anemometer. We place the analysis in the framework of wavepackets and linear stability theory, whence we show, using solutions of the linear parabolised stability equations, that the quieter flows can be understood to result from a mean-flow deformation that modifies wavepacket dynamics, and in particular their phase velocities, which are significantly reduced. 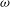The mean-flow deformation is shown, by a triple decomposition, to be due to the generation of Reynolds stresses associated with incoherent turbulence (rather than coherent structures) which arises when the actuation energises the flow with a frequency–azimuthal wavenumber (${\it\omega}$–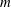$m$) combination to which the mean flow is stable. When the actuation excites the flow with an 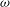${\it\omega}$–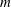$m$ combination to which the mean flow is unstable, the response is dominated by coherent structures, whose rapid growth takes them beyond the linear limit, where they undergo quadratic wave interactions and lead, consequently, to a louder flow.

JFM classification

Acoustics: Aeroacoustics Acoustics: Jet noise Acoustics: Noise control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 788 , 10 February 2016 , pp. 358 - 380
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Breakey, D. E. S., Jordan, P., Cavalieri, A. V. G., Léon, O., Zhang, M., Lehnasch, G., Colonius, T. & Rodriguez, D. 2013 Near-field wavepackets and the far-field sound of a subsonic jet. In 19th AIAA/CEAS Aeroacoustics Conference, AIAA Paper, 2013-2083.Google Scholar
Bridges, J. & Brown, C. A. 2004 Parametric testing of chevrons on single flow hot jets. AIAA Paper 2004–2824.Google Scholar
Bridges, J. E. & Hussain, A. K. M. F. 1987 Roles of initial condition and vortex pairing in jet noise. J. Sound Vib. 117 (2), 289–311.Google Scholar
Butler, G. W. & Calkins, F. T. 2003 Initial attempts to suppress jet noise using piezoelectric actuators. AIAA Paper 2003-3192.Google Scholar
Cavalieri, A. V. G., Daviller, G., Comte, P., Jordan, P., Tadmor, G. & Gervais, Y. 2011a Using large eddy simulation to explore sound-source mechanisms in jets. J. Sound Vib. 330 (17), 4098–4113.Google Scholar
Cavalieri, A. V. G., Jordan, P., Agarwal, A. & Gervais, Y. 2011b Jittering wave-packet models for subsonic jet noise. J. Sound Vib. 330 (18), 4474–4492.CrossRefGoogle Scholar
Cavalieri, A. V. G., Jordan, P., Colonius, T. & Gervais, Y. 2012a Axisymmetric superdirectivity in subsonic jets. J. Fluid Mech. 704, 388–420.CrossRefGoogle Scholar
Cavalieri, A. V. G., Rodriguez, D., Jordan, P., Colonius, T. & Gervais, Y. 2012b Wavepackets in the velocity field of turbulent jets. In 18th AIAA/CEAS Aeroacoustics Conference and Exhibit, Colorado Springs, CO, USA.Google Scholar
Cavalieri, A. V. G., Rodríguez, D., Jordan, P., Colonius, T. & Gervais, Y. 2013 Wavepackets in the velocity field of turbulent jets. J. Fluid Mech. 730, 559–592.CrossRefGoogle Scholar
Crighton, D. G. 1975 Basic principles of aerodynamic noise generation. Prog. Aerosp. Sci. 16, 31–96.Google Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77 (2), 387–413.CrossRefGoogle Scholar
Crighton, D. G. & Huerre, P. 1990 Shear layer pressure fluctuations and superdirective acoustic sources. J. Fluid Mech. 220, 355–368.Google Scholar
Crow, S. C. 1972 Acoustic gain of a turbulent jet. In Phys. Soc. Meeting, Univ. Colorado, Boulder, Paper IE, vol. 6.Google Scholar
Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48, 547–591.CrossRefGoogle Scholar
Ffowcs-Williams, J. E. & Kempton, A. J. 1978 The noise from the large-scale structure of a jet. J. Fluid Mech. 84, 673–694.Google Scholar
Freund, J. B. 2001 Noise sources in a low-Reynolds-number turbulent jet at Mach 0.9. J. Fluid Mech. 438, 277–305.CrossRefGoogle Scholar
Gudmundsson, K. & Colonius, T. 2007 Spatial stability analysis of chevron jet profiles. AIAA Paper 3599, 8–10.Google Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.CrossRefGoogle Scholar
Gutmark, E. J. & Grinstein, F. F. 1999 Flow control with noncircular jets 1. Annu. Rev. Fluid Mech. 31 (1), 239–272.Google Scholar
Henderson, B. 2010 Fifty years of fluidic injection for jet noise reduction. Intl J. Aeroacoust. 9, 91–122.Google Scholar
Herbert, T. 1997 Parabolized stability equations. Annu. Rev. Fluid Mech. 29 (1), 245–283.Google Scholar
Hussain, A. K. M. F. & Reynolds, W. C. 1970 The mechanics of an organized wave in turbulent shear flow. J. Fluid Mech. 41, 241–258.Google Scholar
Hussain, A. K. M. F. & Zaman, K. B. M. Q. 1981 The ‘preferred mode’ of the axisymmetric jet. J. Fluid Mech. 110 (1), 39–71.Google Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45, 173–195.Google Scholar
Juvé, D., Sunyach, M. & Comte-Bellot, G. 1979 Filtered azimuthal correlations in the acoustic far field of a subsonic jet. AIAA J. 17 (1), 112–113.Google Scholar
Kerhervé, F., Jordan, P., Cavalieri, A. V. G., Delville, J., Bogey, C. & Juvé, D. 2012 Educing the source mechanism associated with downstream radiation in subsonic jets. J. Fluid Mech. 710, 606–640.Google Scholar
Kim, K., Kasnakolu, C., Serrani, A. & Samimy, M. 2009 Extremum-seeking control of subsonic cavity flow. AIAA J. 47 (1), 195–205.Google Scholar
Kœnig, M.2011 Réduction de bruit de jet par injection fluidique en corps central tournant (in French). PhD thesis, ENSIP – Université de Poitiers.Google Scholar
Kopiev, V., Chernyshev, S., Faranosov, G., Zaitsev, M. & Belyaev, I. 2010 Correlations of jet noise azimuthal components and their role in source identification. In 16th AIAA/CEAS Aeroacoustics Conference (31st AIAA Aeroacoustics Conference).Google Scholar
Lau, J. C., Fisher, M. J. & Fuchs, H. V. 1972 The intrinsic structure of turbulent jets. J. Sound Vib. 22 (4), 379–406.CrossRefGoogle Scholar
Laufer, J. & Yen, T.-C. 1983 Noise generation by a low-Mach-number jet. J. Fluid Mech. 134, 1–31.CrossRefGoogle Scholar
Liu, J. T. C. 1974 Developing large-scale wavelike eddies and the near jet noise field. J. Fluid Mech. 62 (03), 437–464.CrossRefGoogle Scholar
Mankbadi, R. & Liu, J. T. C. 1984 Sound generated aerodynamically revisited: large-scale structures in a turbulent jet as a source of sound. Phil. Trans. R. Soc. Lond. A 311 (1516), 183–217.Google Scholar
Maury, R., Koenig, M., Cattafesta, L., Jordan, P. & Delville, J. 2012 Extremum-seeking control of jet noise. Intl J. Aeroacoust. 11 (3), 459–474.Google Scholar
Maury, R., Koenig, M., Cattafesta, L., Jordan, P., Delville, J., Bonnet, J. P. & Gervais, Y. 2009 Extremum-seeking optimisation of fluidic jet noise control. In 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference).Google Scholar
Michalke, A. 1970 A wave model for sound generation in circular jets. Deutsche Forschungs- und Versuchsanstalt für Luft- und Raumfa (Cologne), ID.Google Scholar
Michalke, A. 1971 Instabilitat eines kompressiblen runden Freistrahls unter Berucksichtigung des Einflusses der Strahlgrenzschichtdicke. Z. Flugwiss. English translation: NASA TM 75190, 1977 19, 311–328.Google Scholar
Michalke, A. & Fuchs, H. V. 1975 On turbulence and noise of an axisymmetric shear flow. J. Fluid Mech. 70, 179–205.Google Scholar
Mollo-Christensen, E.1963 Measurements of near field pressure of subsonic jets. Tech. Rep., DTIC Document.Google Scholar
Mollo-Christensen, E. 1967 Jet noise and shear flow instability seen from an experimenter’s viewpoint. J. Appl. Mech. 34 (1), 1–7.Google Scholar
Moore, C. J. 1977 The role of shear-layer instability waves in jet exhaust noise. J. Fluid Mech. 80, 321–367.CrossRefGoogle Scholar
Rodríguez, D., Cavalieri, A. V. G., Colonius, T. & Jordan, P. 2015 A study of linear wavepacket models for subsonic turbulent jets using local eigenmode decomposition of PIV data. Eur. J. Mech. (B/Fluids) 49, 308–321.Google Scholar
Rodrıguez, D., Sinha, A., Bres, G. A. & Colonius, T. 2013 Acoustic field associated with parabolized stability equation models in turbulent jets. In 19th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), 27–29 May 2013, Berlin, Germany.Google Scholar
Samimy, M., Kim, J.-H., Kastner, J., Adamovich, I. & Utkin, Y. 2007 Active control of high-speed and high-Reynolds-number jets using plasma actuators. J. Fluid Mech. 578, 305–330.CrossRefGoogle Scholar
Sandham, N., Morfey, C. & Hu, Z. 2006 Sound radiation from exponentially growing and decaying waves. J. Sound Vib. 294, 355–361.Google Scholar
Sasaki, K.2014 Estudo e controle de pacotes de onda em jatos utilizando as equações de estabilidade parabolizadas (in Portuguese). Masters thesis, ITA – Instituto Tecnológico de Aeronáutica, São José dos Campos.Google Scholar
Suponitsky, V., Sandham, N. D. & Morfey, C. L. 2010 Linear and nonlinear mechanisms of sound radiation by instability waves in subsonic jets. J. Fluid Mech. 658, 509–538.Google Scholar
Tam, C. K. W. & Morris, P. J. 1980 The radiation of sound by the instability waves of a compressible plane turbulent shear layer. J. Fluid Mech. 98 (02), 349–381.CrossRefGoogle Scholar
Tutkun, M., George, W. K., Foucaut, J. M., Coudert, S., Stanislas, M. & Delville, J. 2009 In situ calibration of hot wire probes in turbulent flows. Exp. Fluids 46 (4), 617–629.CrossRefGoogle Scholar
Wei, M. & Freund, J. 2006 A noise controlled free shear flow. J. Fluid Mech. 546, 123–152.Google Scholar
Zaman, K. B. M. Q., Bridges, J. E. & Huff, D. L. 2011 Evolution from tabs to chevron technology – a review. Intl J. Aeroacoust. 10 (5), 685–710.Google Scholar
Zhang, M., Jordan, P., Lehnasch, G., Cavalieri, A. V. G. & Agarwal, A.2012 Just enough jitter for jet noise? AIAA Paper 2014-3061.Google Scholar
Zhang, M., Tissot, G., Jordan, P., Lehnasch, G., Cavalieri, A., Colonius, T. & Bres, G. 2015 Non-linear wavepacket forcing for jet noise. In 21st AIAA/CEAS Aeroacoustics Conference Aviation Forum 2015.Google Scholar
Zhang, M., Towne, A., Jordan, P., Colonius, T., Lele, S. et al. 2014 Sound amplification by jittering wavepackets in subsonic turbulent jets. Bull Am. Phys. Soc. 59 (20).Google Scholar