Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T13:27:13.754Z Has data issue: false hasContentIssue false
  • English
  • Français

A kinetic model for particle–surface interaction applied to rain falling on water waves

Published online by Cambridge University Press:  11 May 2016

Fabrice Veron  and
Luc Mieussens
Fabrice Veron*
Affiliation:
School of Marine Science and Policy, University of Delaware, Newark, DE 19716, USA
Luc Mieussens
Affiliation:
Université de Bordeaux, IMB, UMR 5251, F-33400 Talence, France
*
†Email address for correspondence: fveron@udel.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a model for estimating the momentum flux from water drops falling onto a moving free surface. The theory is based on a kinetic approach whereby individual drops are modelled as point particles with mass and velocity, and are described collectively by a distribution function 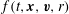$f(t,\boldsymbol{x},\boldsymbol{v},r)$. We show that the resulting momentum flux can be readily incorporated into free-surface Navier–Stokes and Euler models. As an illustration of this approach we examine the interaction between rainfall and linear deep-water surface waves. This particular application is not fundamentally different from the study of Le Méhauté & Khangaonkar (J. Phys. Oceanogr., vol. 20 (12), 1990, pp. 1805–1812), but our methodology is more general and is novel in its use of a kinetic approach with an all-purpose drop distribution function. The applicability of the model to linear surface waves is found to be valid for surface-wave wavelengths ranging from approximately 3 to 250 m. We further show that rainfall modifies the usual wave dispersion relationship and induces wave amplification, or damping, depending on the rain rate, the rain impact angle and the wavelength of the surface wave. We solve for the amplification and damping rates analytically and show, among other results, that rain falling vertically will always damp the surface waves.

JFM classification

Geophysical and Geological Flows: Air/sea interactions Drops and Bubbles: Drops Waves/Free-surface Flows: Surface gravity waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 796 , 10 June 2016 , pp. 767 - 787
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atlas, D. 1994 Footprints of storms on the sea: a view from spaceborne synthetic aperture radar. J. Geophys. Res. 99 (C4), 7961–7969.Google Scholar
Best, A. C. 1950 Empirical formulae for the terminal velocity of water drops falling through the atmosphere. Q. J. R. Meteorol. Soc. 76, 302–311.Google Scholar
Beya, J., Peirson, W. & Banner, M. 2011 Rainfall-generated, near-surface turbulence. In Gas Transfers at Water Surfaces 2010 (ed. Komori, S., McGillis, W. & Kurose, R.), pp. 90–103. Kyoto University Press.Google Scholar
Bliven, L., Branger, H., Sobieski, P. & Giovanangeli, J. P. 1993 An analysis of scatterometer returns from a water agitated by artificial rain. Intl J. Remote Sens. 14 (12), 2315–2329.Google Scholar
Bliven, L. F., Sobieski, P. W. & Craeye, C. 1997 Rain generated ring-waves: measurements and modelling for remote sensing. Intl J. Remote Sens. 18 (1), 221–228.Google Scholar
Braun, N.2003 Untersuchungen zur radar-rückstreuung und wellendämpfung beregneter wasseroberflächen [On the radar backscattering and wave damping on water surfaces agitated by rain]. PhD dissertation, University of Hamburg (in German).Google Scholar
Braun, N., Gade, M. & Lange, P. A. 2002 The effect of artificial rain on wave spectra and multi-polarisation x band radar backscatter. Intl J. Remote Sens. 23 (20), 4305–4323.CrossRefGoogle Scholar
Caldwell, D. R. & Elliott, W. P. 1971 Surface stresses produced by rainfall. J. Phys. Oceanogr. 1 (2), 145–148.Google Scholar
Caldwell, D. R. & Elliott, W. P. 1972 The effect of rainfall on the wind in the surface layer. Boundary-Layer Meteorol. 3 (2), 146–151.Google Scholar
Chapman, S. & Cowling, T. G. 1990 The Mathematical Theory of Nonuniform Gases, 3rd edn. Cambridge University Press.Google Scholar
Chen, G., Chapron, B., Tournadre, J., Katsaros, K. & Vandemark, D. 1998 Identification of possible wave damping by rain using topex and tmr data. Remote Sens. Environ. 63 (1), 40–48.Google Scholar
Contreras, R. F., Plant, W. J., Keller, W. C., Hayes, K. & Nystuen, J. 2003 Effects of rain on Ku-band backscatter from the ocean. J. Geophys. Res. 108 (C5), 3165.Google Scholar
Csanady, G. T. 2001 Air–Sea Interaction Laws and Mechanisms. Cambridge University Press.Google Scholar
Green, T. & Houk, D. F. 1979 The mixing of rain with near-surface water. J. Fluid Mech. 90, 569–588.CrossRefGoogle Scholar
Guymer, T. H., Quartly, G. D. & Srokosz, M. A. 1995 The effects of rain on ERS-1 radar altimeter data. J. Atmos. Ocean. Technol. 12, 1229–1247.Google Scholar
Harrison, E. L.2012 The effects of rainfall in the ocean surface at low to moderate wind speed. PhD dissertation, University of Delaware.Google Scholar
Harrison, E. L., Veron, F., Ho, D. T., Reid, M. S., Orton, P. & McGillis, W. R. 2012 Nonlinear interaction between rain- and wind-induced air–water gas exchange. J. Geophys. Res. 117, C03034.Google Scholar
Ho, D. T., Asher, W. E., Bliven, L. F., Schlosser, P. & Gordan, E. L. 2000 On mechanisms of rain-induced air–water gas exchange. J. Geophys. Res. 105 (C10), 24045–24057.CrossRefGoogle Scholar
Jones, I. S. F. & Toba, Y. 2001 Wind Stress Over the Ocean. Cambridge University Press.Google Scholar
Kraus, E. B. & Bussinger, J. A. 1994 Atmosphere–Ocean Interaction. Oxford University Press.Google Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
Law, J. O. & Parsons, D. A. 1943 The relation of raindrop-size intensity. Trans. Am. Geophys. Union 24, 452–460.Google Scholar
Le Méhauté, B. & Khangaonkar, T. 1990 Dynamic interaction of intense rain with water waves. J. Phys. Oceanogr. 20 (12), 1805–1812.2.0.CO;2>CrossRefGoogle Scholar
Manton, M. J. 1973 On the attenuation of sea waves by rain. Geophys. Astrophys. Fluid Dyn. 5, 249–260.CrossRefGoogle Scholar
Marchiso, E. & Fox, R. O. 2013 Computational Models for Polydisperse Particulate and Multiphase Systems. Cambridge University Press.Google Scholar
Marshall, J. S. & Palmer, W. M. K. 1948 The distribution of raindrops with size. J. Meteorol. 5, 165–166.Google Scholar
Melville, W. K. 1996 The role of surface-wave breaking in air–sea interaction. Annu. Rev. Fluid Mech. 28, 279–321.Google Scholar
Mueller, J. A. & Veron, F. 2009 A lagrangian stochastic model for heavy particle dispersion in the atmospheric marine boundary layer. Boundary-Layer Meteorol. 130 (2), 229–247.Google Scholar
Nystuen, J. A. 1990 A note on the attenuation of surface gravity waves by rainfall. J. Geophys. Res. 95 (C10), 18353–18355.CrossRefGoogle Scholar
Peirson, W. L., Beya, J. F., Banner, M. L., Peral, J. S. & Azarmsa, S. A. 2013 Rain-induced attenuation of deep-water waves. J. Fluid Mech. 724, 5–35.Google Scholar
Phillips, O. M. 1987 Ocean-wave predictions: where are we? In Proc. Symp. Measuring Ocean Waves from Space, vol. 8, pp. 7–10. The Johns Hopkins University APL Technical Digest.Google Scholar
Poon, Y. K., Tang, S. & Wu, J. 1992 Interactions between rain and wind waves. J. Phys. Oceanogr. 22 (9), 976–987.Google Scholar
Prosperetti, A. & Oguz, H. N. 1993 The impact of drops on liquid surfaces and the underwater noise of rain. Annu. Rev. Fluid Mech. 25, 577–602.Google Scholar
Quartly, G. D., Guymer, T. H. & Srokosz, M. A. 1996 The effects of rain on topex radar altimeter data. J. Atmos. Ocean. Technol. 13, 1209–1229.Google Scholar
Reynolds, O. 1900 On the action of rain to calm the sea. Papers on Mechanical and Physical Subjects 1870–1880. Collected Works. vol. 1, pp. 86–88. Cambridge University Press.Google Scholar
Schlussel, P., Soloviev, A. V. & Emery, W. J. 1997 Cool and freshwater skin of the ocean during rainfall. Boundary-Layer Meteorol. 82 (3), 439–474.Google Scholar
Sullivan, P. P. & McWilliams, J. C. 2010 Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42.Google Scholar
Teixeira, M. A. C. & Belcher, S. E. 2002 On the distortion of turbulence by a progressive surface wave. J. Fluid Mech. 458, 229–267.CrossRefGoogle Scholar
Thorpe, S. A. 2004 Langmuir circulation. Annu. Rev. Fluid Mech. 36, 55–79.CrossRefGoogle Scholar
Tsimplis, M. N. 1992 The effect of rain in calming the sea. J. Phys. Oceanogr. 22 (4), 404–412.Google Scholar
Tsimplis, M. & Thorpe, S. A. 1989 Wave damping by rain. Nature 342, 893–895.Google Scholar
Ulbrich, C. W. 1983 Natural variations in the analytical form of the raindrop size distribution. J. Clim. Appl. Meteorol. 22, 1764–1775.2.0.CO;2>CrossRefGoogle Scholar
Veron, F. 2015 Ocean spray. Annu. Rev. Fluid Mech. 47, 507–538.Google Scholar
Villermaux, E. & Bossa, B. 2009 Single-drop fragmentation distribution of raindrops. Nat. Phys. 5 (9), 697–702.Google Scholar
Weissman, D. E., Stiles, B. W., Hristova-Veleva, S. M., Long, D. G., Smith, D. K., Hilburn, K. A. & Jones, L. W. 2012 Challenges to satellite sensors of ocean winds: addressing precipitation effects. J. Atmos. Ocean. Technol. 29, 356–374.Google Scholar
de Wolf, D. A. 2001 On the Laws–Parsons distribution of raindrop sizes. Radio Sci. 36 (4), 639–642.Google Scholar
Yang, Z., Tang, S. & Wu, J. 1997 An experimental study of rain effects on fine structures of wind waves. J. Phys. Oceanogr. 27 (3), 419–430.Google Scholar
Yarin, A. L. 2005 Drop impact dynamics: splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 38, 159–192.Google Scholar