Article contents
Laminar and transitional liquid metal duct flow near a magnetic point dipole
Published online by Cambridge University Press: 28 October 2013
Abstract
The flow transformation and the generation of vortex structures by a strong magnetic dipole field in a liquid metal duct flow is studied by means of three-dimensional direct numerical simulations. The dipole is considered as the paradigm for a magnetic obstacle which will deviate the streamlines due to Lorentz forces acting on the fluid elements. The duct is of square cross-section. The dipole is located above the top wall and is centred in spanwise direction. Our model uses the quasistatic approximation which is applicable in the limit of small magnetic Reynolds numbers. The analysis covers the stationary flow regime at small hydrodynamic Reynolds numbers 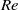 $\mathit{Re}$ as well as the transitional time-dependent regime at higher values which may generate a turbulent flow in the wake of the magnetic obstacle. We present a systematic study of these two basic flow regimes and their dependence on
$\mathit{Re}$ as well as the transitional time-dependent regime at higher values which may generate a turbulent flow in the wake of the magnetic obstacle. We present a systematic study of these two basic flow regimes and their dependence on 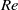 $\mathit{Re}$ and on the Hartmann number
$\mathit{Re}$ and on the Hartmann number 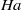 $\mathit{Ha}$, a measure of the strength of the magnetic dipole field. Furthermore, three orientations of the dipole are compared: streamwise-, spanwise- and wall-normal-oriented dipole axes. The most efficient generation of turbulence at a fixed distance above the duct follows for the spanwise orientation, which is caused by a certain configuration of Hartmann layers and reversed flow at the top plate. The enstrophy in the turbulent wake grows linearly with
$\mathit{Ha}$, a measure of the strength of the magnetic dipole field. Furthermore, three orientations of the dipole are compared: streamwise-, spanwise- and wall-normal-oriented dipole axes. The most efficient generation of turbulence at a fixed distance above the duct follows for the spanwise orientation, which is caused by a certain configuration of Hartmann layers and reversed flow at the top plate. The enstrophy in the turbulent wake grows linearly with 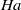 $\mathit{Ha}$ which is connected with a dominance of the wall-normal derivative of the streamwise velocity.
$\mathit{Ha}$ which is connected with a dominance of the wall-normal derivative of the streamwise velocity.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 10
- Cited by


