Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T06:30:30.908Z Has data issue: false hasContentIssue false
  • English
  • Français

The laminar free surface boundary layer of a solitary wave

Published online by Cambridge University Press:  06 March 2012

Christian A. Klettner  and
Ian Eames
Christian A. Klettner*
Affiliation:
University College London, Torrington Place, London WC1E 7JE, UK
Ian Eames
Affiliation:
University College London, Torrington Place, London WC1E 7JE, UK
*
†Email address for correspondence: christian_klettner@nuhs.edu.sg
Get access Rights & Permissions [Opens in a new window]

Abstract

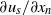The laminar free surface boundary layer beneath a solitary wave is investigated using numerical simulations. Across the boundary layer and 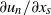are comparable in magnitude, where is the velocity, position and subscripts and refer to components tangential and normal to the free surface. In this region 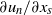is approximately constant across the boundary layer while 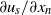varies with 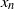and outside the boundary layer tends to 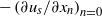. The numerical results are compared to analytical models and good agreement is found.

JFM classification

Boundary Layers: Boundary layer structure Waves/Free-surface Flows: Solitary waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 696 , 10 April 2012 , pp. 423 - 433
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: National University Hospital Singapore, 5 Lower Kent Ridge Rd, Main Building 1, Singapore 119074.

References

1. Batchelor, G. K. 1967 An Introduction to Fluid Dynamics, 1st edn. Cambridge University Press.Google Scholar
2. Grimshaw, R. 1971 The solitary wave in water of variable depth. J. Fluid Mech. 46, 611–622.CrossRefGoogle Scholar
3. Hirt, C. W., Amsden, A. A. & Cook, J. L. 1974 An arbitrary Lagrangian–Eulerian computing method for all flow speeds. J. Comput. Phys. 14, 227–253.CrossRefGoogle Scholar
4. Hunt, J. C. R. & Eames, I. 2002 The disappearance of viscous and laminar wakes in complex flows. J. Fluid Mech. 457, 111–132.CrossRefGoogle Scholar
5. Jonsson, I. G., Thorup, P. & Tamasauskas, H. T. 2000 Accuracy of asymptotic series for the kinematics of high solitary waves. Ocean Engng 27, 511–529.CrossRefGoogle Scholar
6. Klettner, C. A. 2010On the fundamental principles of waves propagating over complex geometry. PhD thesis, University College London.Google Scholar
7. Lamb, H. 1932 Hydrodynamics, 6th edn. Cambridge University Press.Google Scholar
8. Lin, P. & Zhang, W. 2008 Numerical simulation of wave-induced laminar boundary layers. Ocean Engng 55, 400–408.Google Scholar
9. Liu, P. L. F., Park, Y. S. & Cowen, E. A. 2007 Boundary layer flow and bed shear stress under a solitary wave. J. Fluid Mech. 574, 449–463.CrossRefGoogle Scholar
10. Longuet-Higgins, M. S. 1959 Mass transport in the boundary layer at a free oscillating surface. J. Fluid Mech. 8, 293–306.CrossRefGoogle Scholar
11. Longuet-Higgins, M. S. 1992 Capillary rollers and bores. J. Fluid Mech. 240, 659–679.CrossRefGoogle Scholar
12. Mei, C. C. 1995 Mathematical Analysis in Engineering. Cambridge University Press.CrossRefGoogle Scholar
13. Nithiarasu, P. 2005 An arbitrary Lagrangian Eulerian (ALE) formulation for free surface flows using the characteristic based split (CBS) scheme. Intl J. Numer. Meth. Engng. 48, 1415–1428.CrossRefGoogle Scholar
14. Nithiarasu, P., Mathur, J. S., Weatherill, N. P. & Morgan, K. 2004 Three-dimensional incompressible flow calculations using the characteristic based split (CBS) scheme. Intl J. Numer. Meth. Fluids 44, 1207–1229.CrossRefGoogle Scholar
15. Prosperetti, A. & Tryggvason, G. 2007 Computational Methods for Multiphase Flow. Cambridge University Press.CrossRefGoogle Scholar
16. Raval, A., Wen, X. & Smith, M. H. 2009 Numerical simulation of viscous, nonlinear and progressive water waves. J. Fluid Mech. 637, 443–473.CrossRefGoogle Scholar
17. Shen, L., Triantafyllou, G. S. & Yue, D. K. 2000 Turbulent diffusion near a free surface. J. Fluid Mech. 407, 145–166.CrossRefGoogle Scholar
18. Shen, L., Zhang, X., Yue, D. K. & Triantafyllou, G. S. 1999 The surface layer for free surface turbulent flows. J. Fluid Mech. 386, 167–212.CrossRefGoogle Scholar
19. Sumer, B. M., Jensen, P. M., Sorensen, L. B., Fredsoe, J. & Liu, P. L. F. 2008 Turbulent solitary wave boundary layer. In Proceedings of the 8th International Offshore and Polar Engineering Conference (ed. J. S. Chung, S. T. Grilli, S. Naito & Q. Ma), pp. 775–781.Google Scholar
20. Tanaka, H., Sumer, B. M. & Lodahl, C. 1998 Theoretical and experimental investigation on laminar boundary layers under cnoidal wave motion. Coast. Engng Japan 40, 81–89.CrossRefGoogle Scholar
21. Vittorio, G. & Blondeaux, P. 2008 Turbulent boundary layer under a solitary wave. J. Fluid Mech. 615, 433–443.CrossRefGoogle Scholar