Article contents
Laminar post-stall wakes of tapered swept wings
Published online by Cambridge University Press: 24 November 2023
Abstract
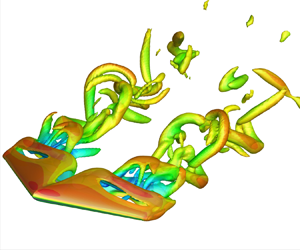
While tapered swept wings are widely used, the influence of taper on their post-stall wake characteristics remains largely unexplored. To address this issue, we conduct an extensive study using direct numerical simulations to characterize the wing taper and sweep effects on laminar separated wakes. We analyse flows behind NACA 0015 cross-sectional profile wings at post-stall angles of attack  $\alpha =14^\circ$–
$\alpha =14^\circ$– $22^\circ$ with taper ratios
$22^\circ$ with taper ratios  $\lambda =0.27$–
$\lambda =0.27$– $1$, leading-edge sweep angles
$1$, leading-edge sweep angles  $0^\circ$–
$0^\circ$– $50^\circ$ and semi aspect ratios
$50^\circ$ and semi aspect ratios  $sAR =1$ and
$sAR =1$ and  $2$ at a mean-chord-based Reynolds number of
$2$ at a mean-chord-based Reynolds number of  $600$. Tapered wings have smaller tip chord length, which generates a weaker tip vortex, and attenuates inboard downwash. This results in the development of unsteadiness over a large portion of the wingspan at high angles of attack. For tapered wings with backward-swept leading edges, unsteadiness emerges near the wing tip. On the other hand, wings with forward-swept trailing edges are shown to concentrate wake-shedding structures near the wing root. For highly swept untapered wings, the wake is steady, while unsteady shedding vortices appear near the tip for tapered wings with high leading-edge sweep angles. For such wings, larger wake oscillations emerge near the root as the taper ratio decreases. While the combination of taper and sweep increases flow unsteadiness, we find that tapered swept wings have more enhanced aerodynamic performance than untapered and unswept wings, exhibiting higher time-averaged lift and lift-to-drag ratio. The current findings shed light on the fundamental aspects of flow separation over tapered wings in the absence of turbulent flow effects.
$600$. Tapered wings have smaller tip chord length, which generates a weaker tip vortex, and attenuates inboard downwash. This results in the development of unsteadiness over a large portion of the wingspan at high angles of attack. For tapered wings with backward-swept leading edges, unsteadiness emerges near the wing tip. On the other hand, wings with forward-swept trailing edges are shown to concentrate wake-shedding structures near the wing root. For highly swept untapered wings, the wake is steady, while unsteady shedding vortices appear near the tip for tapered wings with high leading-edge sweep angles. For such wings, larger wake oscillations emerge near the root as the taper ratio decreases. While the combination of taper and sweep increases flow unsteadiness, we find that tapered swept wings have more enhanced aerodynamic performance than untapered and unswept wings, exhibiting higher time-averaged lift and lift-to-drag ratio. The current findings shed light on the fundamental aspects of flow separation over tapered wings in the absence of turbulent flow effects.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
Footnotes
Present address: Faculdade de Engenharia Mecânica, Universidade Estadual de Campinas, Campinas, SP 13083-860, Brazil.
Present address: Department of Aerospace Engineering and Engineering Mechanics, The University of Texas at Austin, Austin, TX 78712, USA.
Present address: Faculty of Aerospace Engineering, Technion - Israel Institute of Technology, Haifa 32000, Israel.
References
- 9
- Cited by


